Тема 4. Теорія ігор

1. Мета: навчитися зводити матричні ігри до задач ЛП.

2. Завдання 1.

Розв'язати матричні ігри, шляхом зведення до пари двоїстих задач лінійного програмування та методом Брауна-Робiнсона знайти оптимальні змішані стратегії та ціну гри матричних ігор з такими платіжними матрицями:

Приклад. Знайти рішення гри, що визначається матрицею .

Розв’язання. Складемо пару двоїстих задач ЛП. Пряма задача: знайти максимальне значення функції F=x₁+x₂+x₃ при умовах

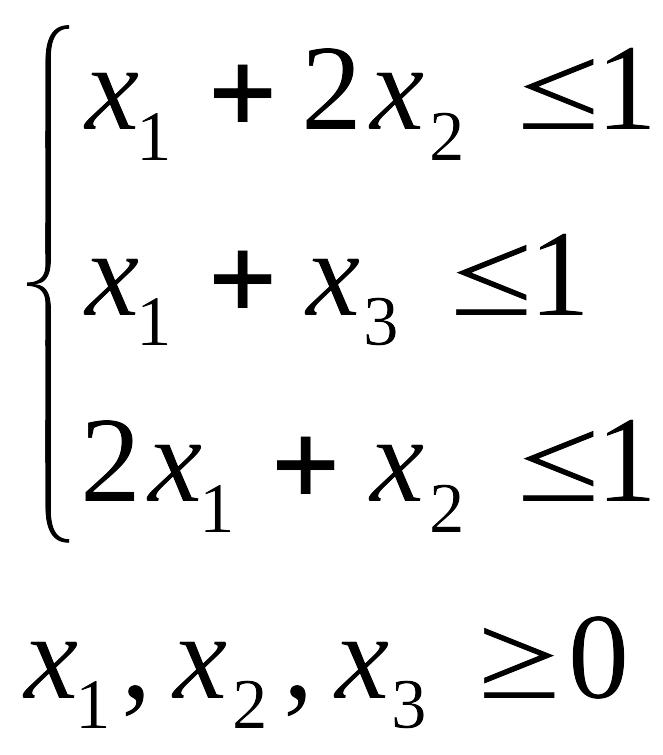
Двоїста задача: знайти мінімум функції F^*=y₁+y₂+y₃ при умовах

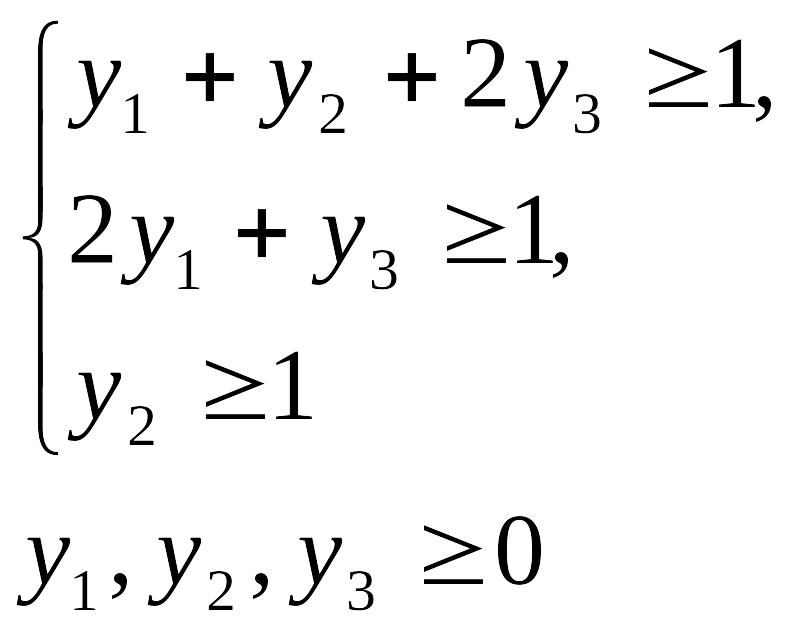
Знаходимо оптимальні плани прямої і двоїстої задач

№	Базис	Сб	Р0	1	1	1	0	0	0
				Х1	Х2	Х3	Х4	Х5	Х6
1	Х2	1	½	½	1	0	½	0	0
2	Х3	1	1	1	0	1	0	1	0
3	Х6	0	½	3/2	0	0	-1/2	0	1
			3/2	1/2	0	0	1/2	1	0

Із останньої симплексної таблиці видно, що вихідна задача має оптимальний план Х^*=(0; 1/2; 1), а двоїста задача оптимальний план У^*=(1/2; 1; 0). Отже, ціна гри 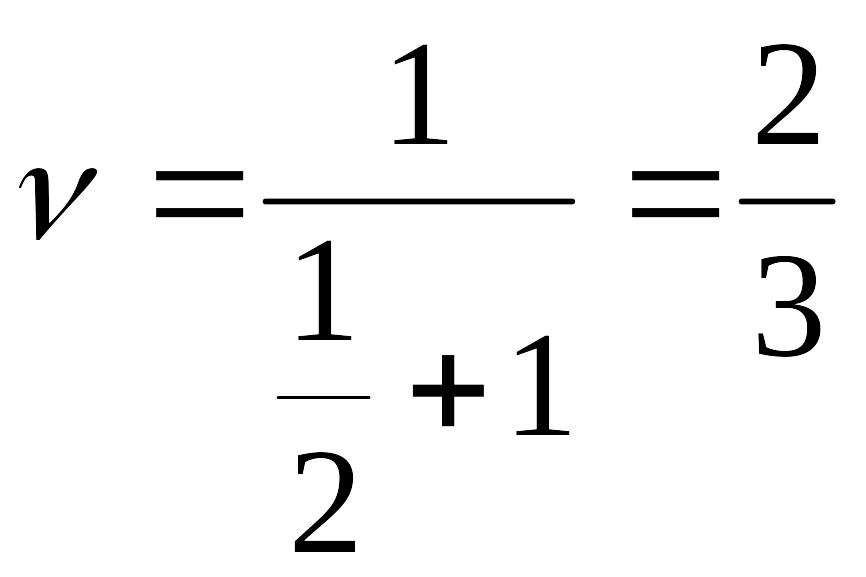, а оптимальні стратегії гравців U^*=(1/3; 2/3; 0); Z^*=(0; 1/3; 2/3).

Приклад: Знайти рішення гри, що задана матрицею .

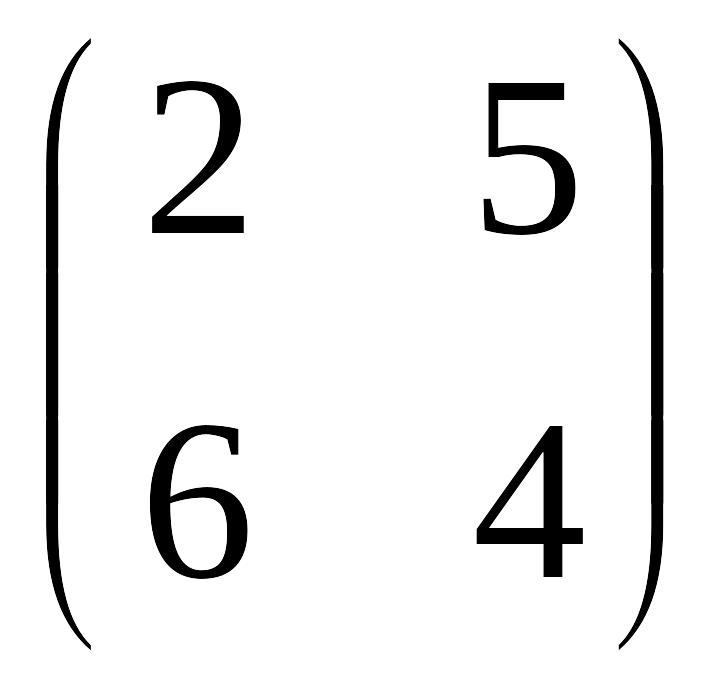Складемо матрицю платежів:

	І	ІІ	мін. рядків
А	2	5	2
В	6	4	4
макс. стовп.	6	5

Максимін , мінімакс . Так як ці величини нерівні між собою, то гра не має рішення в чистих стратегіях. В даному випадку ціна гри знаходиться в інтервалі [4;5].

Припустимо, що для гравця А стратегія задається вектором . Тоді на основі теореми 4 при застосуванні гравцем В чистої стратегії В1 або В2 гравець А отримає середній виграш, який дорівнює ціні гри, тобто:

при стратегії В1

при стратегії В2

Окрім двох записаних рівнянь відносно і добавимо рівняння, що зв’язує частоти і .

.

Розв'зуючи отриману систему рівнянь трьох рівнянь з трьома невідомими, знаходимо , , .

Знайдемо тепер оптимальну стратегію для гравця В. Нехай його стратегія задається вектором . Тоді

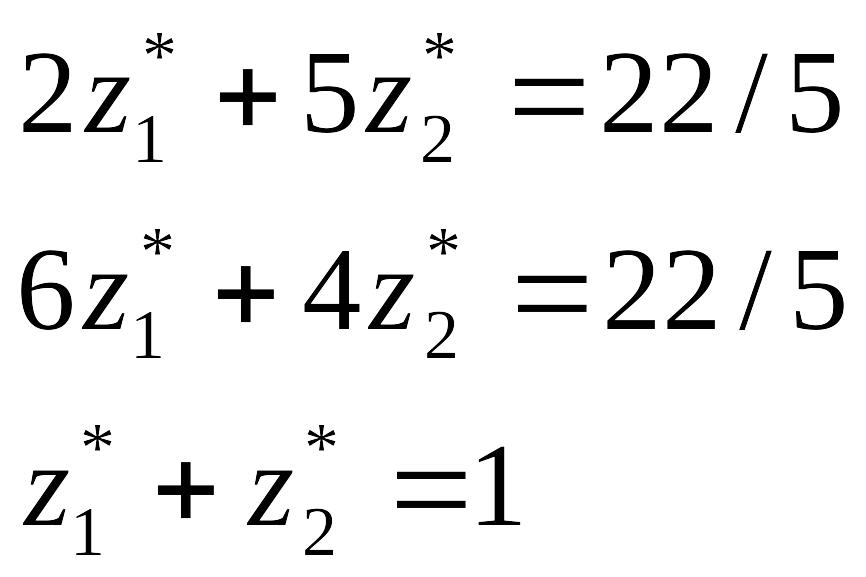
Розв’язуючи систему з двох будь-яких рівнянь, взятих з останньої системи, отримуємо , .

Отже, розв’язком гри є змішані стратегії і , а ціна гри .

Завдання 2. Зведення задач теорії ігор до задач лінійного програмування

Для розв’язання гри засобами лінійного програмування необхідно:

1. Скласти пару двоїстих задачі лінійного програмування відповідно до заданої матриці гри.

   1. Пряма задача: знайти максимальне значення функції 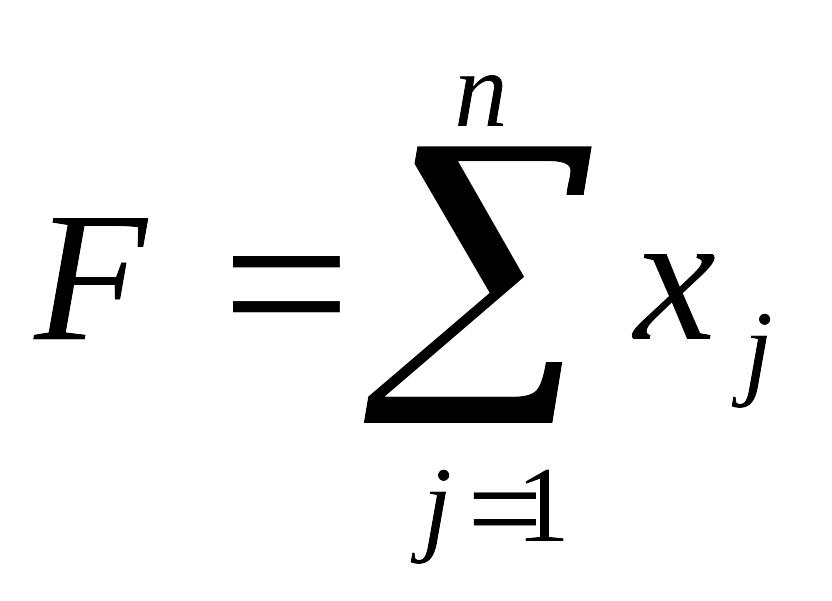за умов .

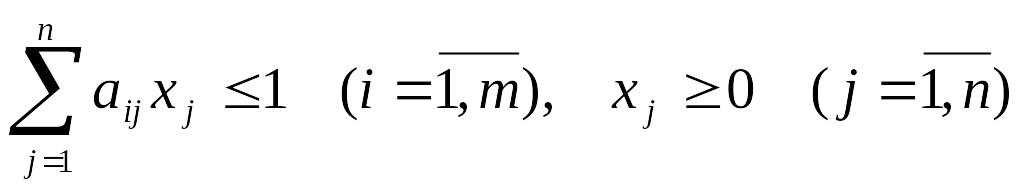   2. Двоїста задача: знайти мінімальне значення функції 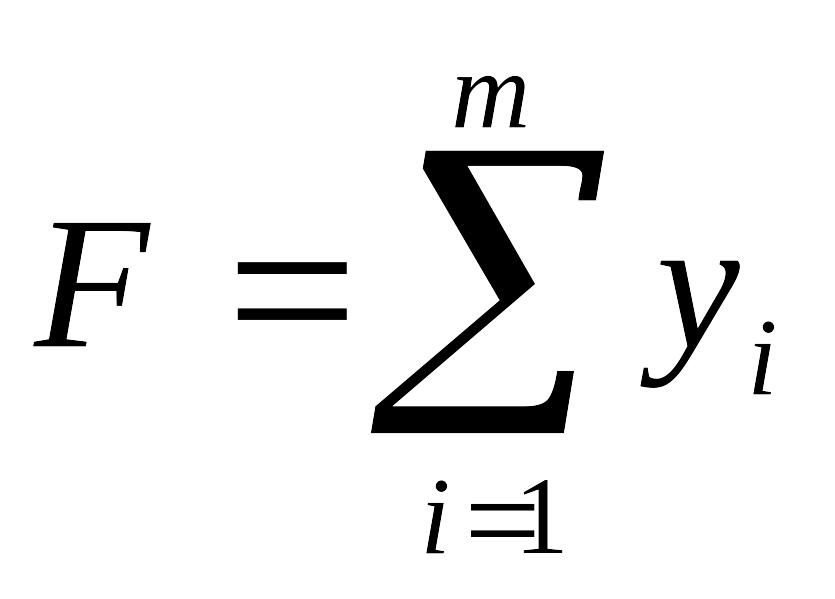за умов .

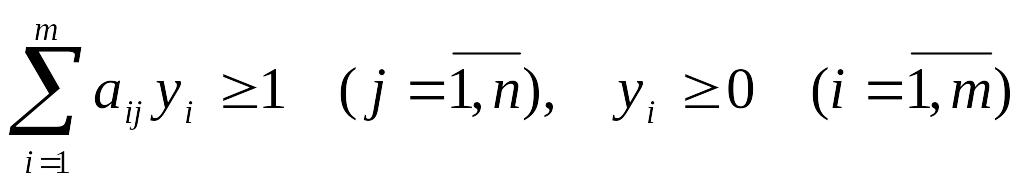2. Знайти оптимальні плани двоїстих задач.

3. Знайти рішення гри, використовуючи співвідношення між планами пари двоїстих задач і оптимальними стратегіями і ціною гри:

( , ).

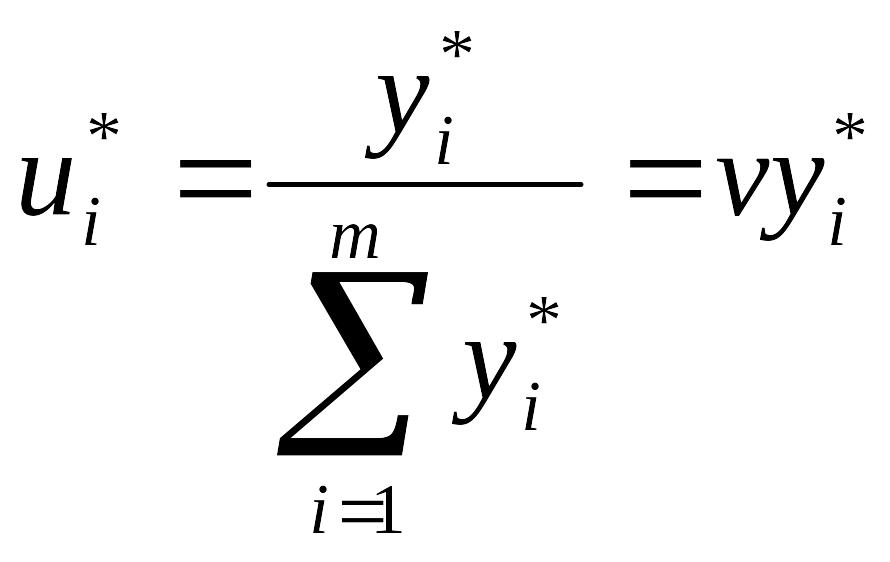
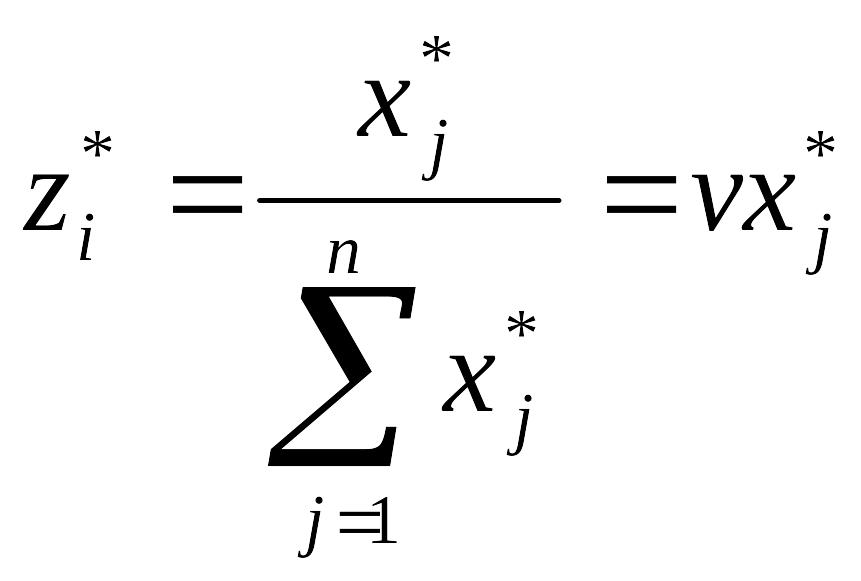
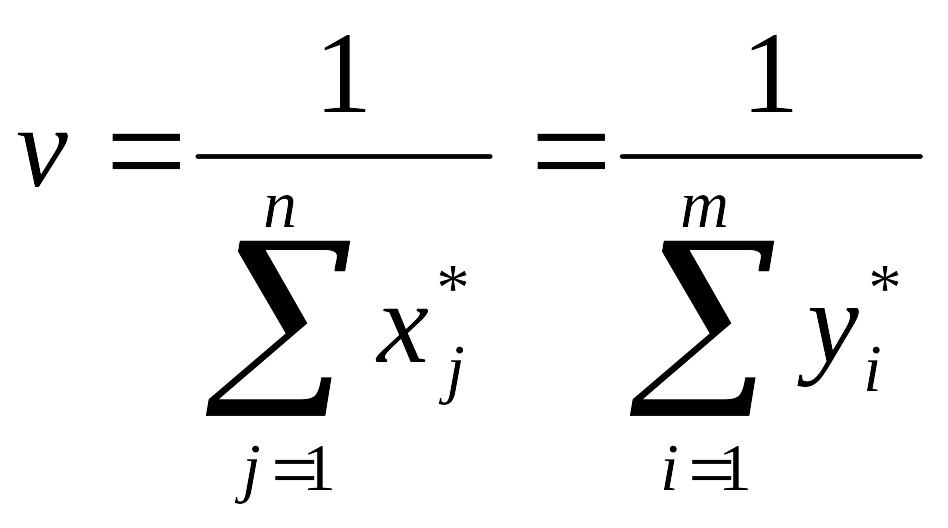Завдання для самостійного розв’язання

Розв’язати задачу теорії ігор шляхом зведення її до задач лінійного програмування. Вхідні дані взяти згідно варіанту з таблиці 4.1.

Сільськогосподарське підприємство може засіяти дослідні поля пшеницею трьох сортів А1, А2, А3. Їх врожайність залежить від багатьох факторів, в тому числі і від погодних умов. Погодні умови характеризуються трьома станами: В1 (засушливе літо), В2 (нормальна кількість опадів), В3 (дощове літо). Для отримання максимального врожаю визначити оптимальні пропорції посівних площ пшениці по видах, якщо відома матриця середньої врожайності:

	В1	В2	В3
А1	а11	а12	а13
А2	а21	а22	а23
А3	а31	а32	а33

Таблиця 4.1.

	а11	а12	а13	а21	а22	а23	а31	а32	а33
1	38	40	42	34	35	30	40	48	26
2	39	41	43	35	36	31	41	49	27
3	40	42	44	36	37	32	42	50	28
4	35	70	50	40	40	38	52	54	48
5	35	40	38	40	60	38	50	46	38
6	35	40	38	62	60	50	50	46	38
7	40	45	35	30	50	45	35	52	40
8	35	45	40	45	50	30	40	52	38
9	44	46	42	45	50	38	40	52	45
10	42	46	44	38	50	45	45	52	40
11	42	46	44	44	50	46	45	52	40
12	40	46	44	48	58	44	48	57	42
13	50	64	42	40	52	50	53	58	50
14	51	65	43	39	51	49	54	57	49
15	49	63	40	40	52	50	52	50	47
16	48	60	42	42	50	52	54	55	52
17	47	55	40	42	52	52	50	58	48
18	48	56	41	41	50	51	51	58	49
19	44	54	46	41	50	51	50	52	48
20	43	53	45	42	51	52	49	51	47
21	42	52	44	41	50	48	48	50	46
22	45	51	43	39	49	44	42	50	48
23	44	50	42	40	50	45	43	51	49
24	46	52	44	38	48	43	44	52	50
25	43	49	41	40	50	45	41	39	37
26	42	49	41	40	46	44	36	39	47
27	42	48	44	40	46	44	44	47	39
28	43	49	45	39	45	43	45	48	40
29	43	49	45	39	45	43	45	48	44
30	45	49	42	39	45	43	45	48	41