Задача 2. Симплексний метод розв’язання задач лінійного програмування. Умова задачі.

Фермер може вирощувати 4 культури на площі 80га. Він вже вклав угоди на продаж певної продукції (обсяг продаж) і може придбати 250ц мінеральних добрив.

Площа просапних культур (соняшник, цукровий буряк, картопля, кукурудза) повинна бути 20 га.

Витрати праці та добрив, прибуток з 1 га наведено в таблиці.

Культури	Урожайність, ц/га	Обсяг продаж, ц	Витрати добрив на 1га, ц	Прибуток, грн./га
Пшениця	30	-	3,5	160
Ячмінь	25	-	3	120
Просо	20	200	3	100
Картопля	330	-	5	260

Визначити, які площі слід відвести під кожну культуру, щоб отримати максимальний прибуток. Розробити економіко-математичну модель та розв’язати задачу.

Рішення

Розробимо економіко-математичну модель задачі.

Змінні:

Х₁ – площа пшениці;

Х₂ – площа ячменю;

Х₃ – площа проса;

Х₄ – площа картоплі.

Цільова функція (максимальний прибуток) буде мати вигляд:

F=160X₁+120X₂+100X₃+260X₄  max

На змінні задачі накладені обмеження:

1-ше обмеження характеризує використання площі ріллі

Х₁ + Х₂ + Х₃ + Х₄ <= 80

2-ге обмеження стосується угоди на продаж проса ( 200 ц):

20 Х ₃ >= 200

3-тє обмеження описує використання добрив

3,5Х₁ + 3Х₂ + 3Х₃ + 5Х₄ <= 250

4-те обмеження описує умову, що площа картоплі повинна бути 20 га:

Х₄ = 20

Запишемо задачу в канонічному вигляді (в кожну нерівність системи обмежень вводяться додаткові змінні, в цільову функцію додаткові змінні вводяться з коефіцієнтом 0).

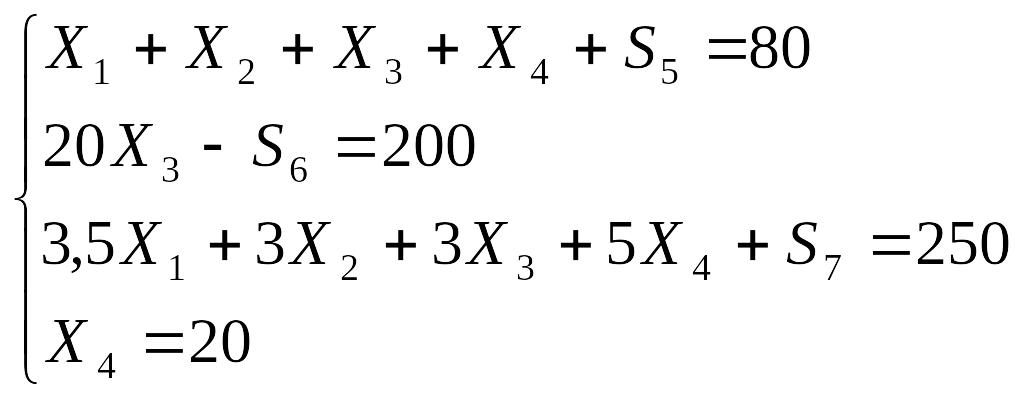
Цільова функція має вигляд:

F=160X₁+120X₂+100X₃+260X₄+0S₅+0S₆+0S₇ max

Обмеження задачі запишемо у векторному вигляді:

; ; ; ; ; ; ;

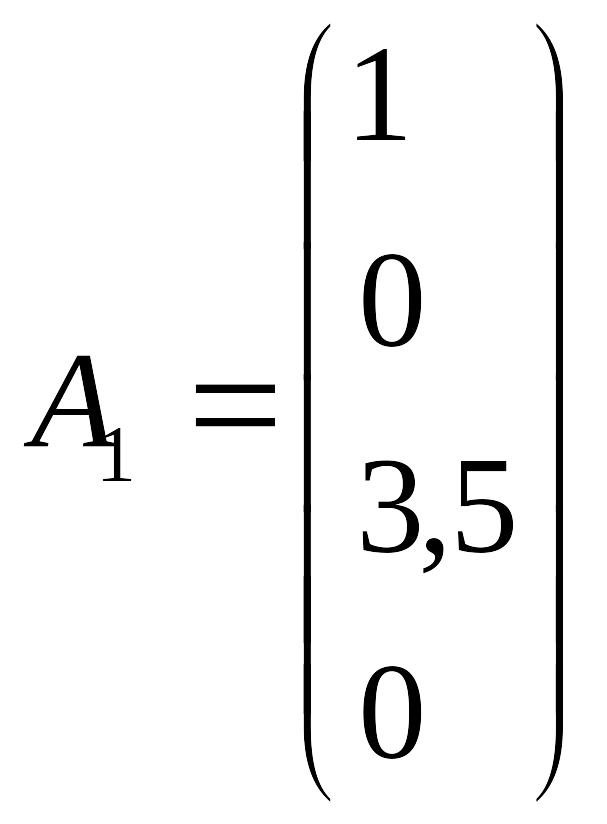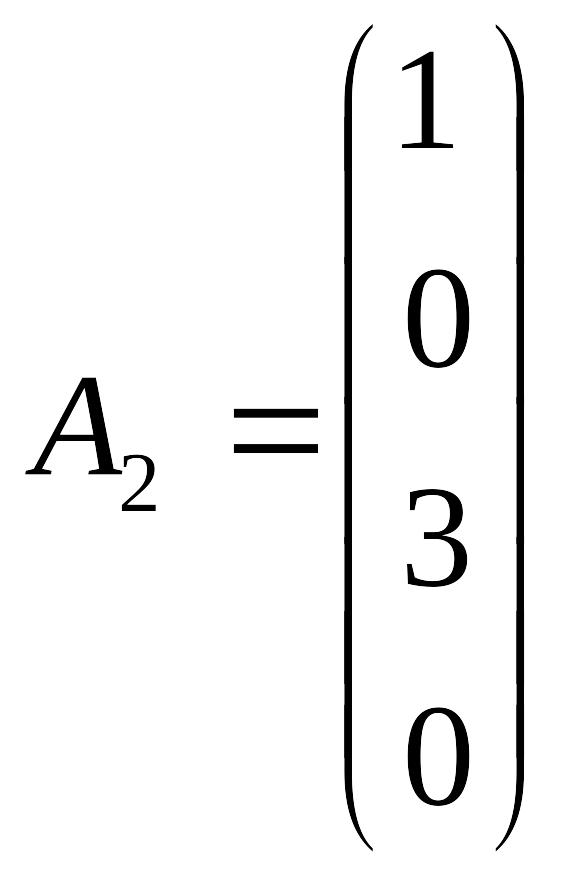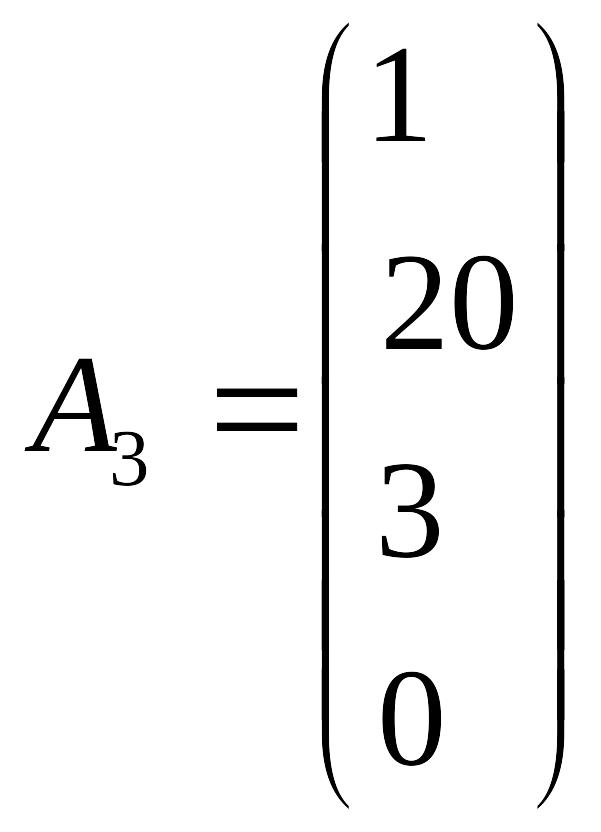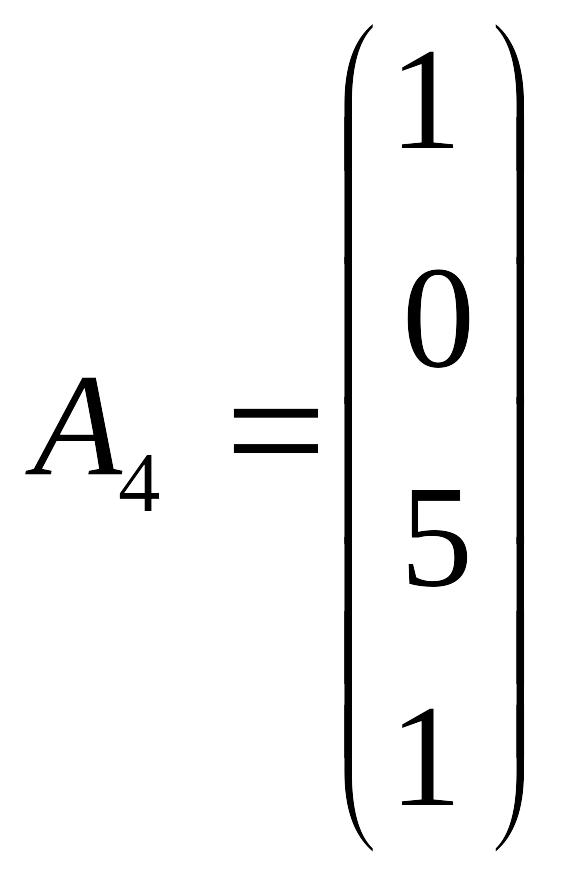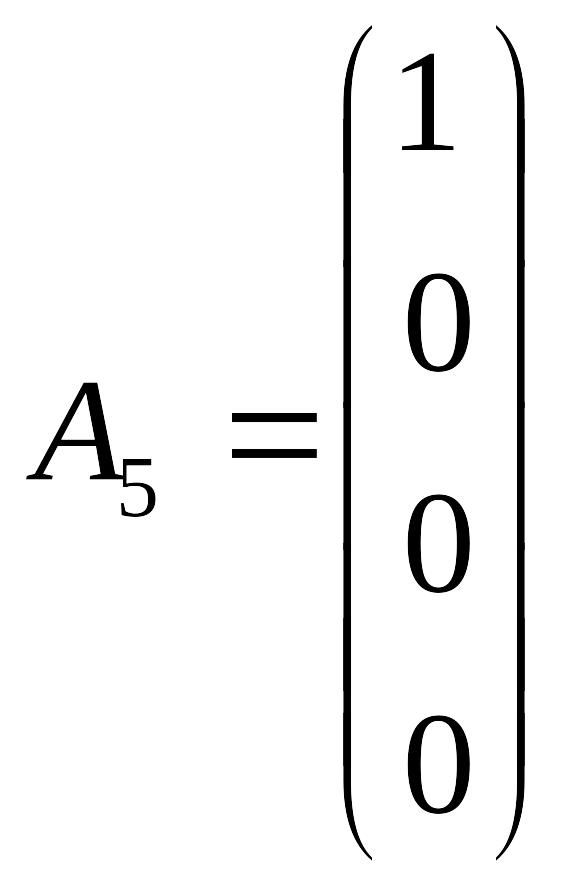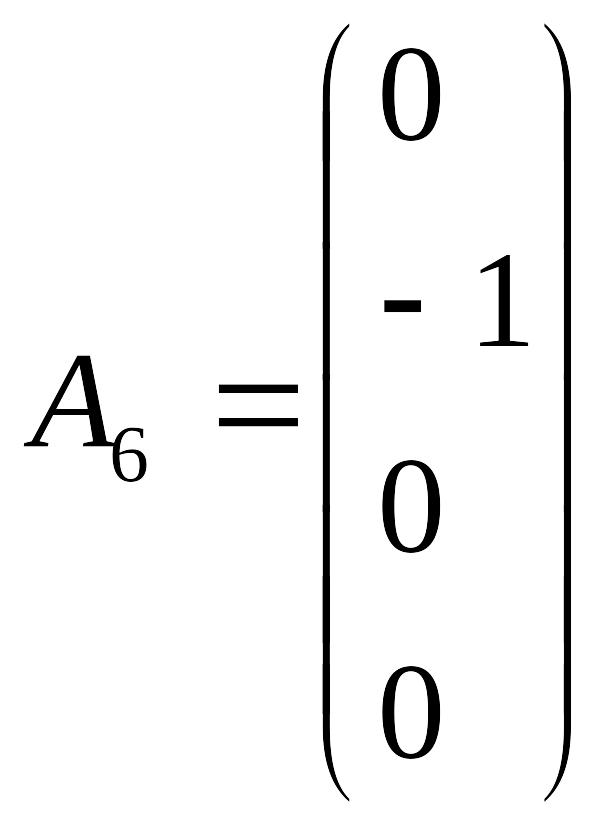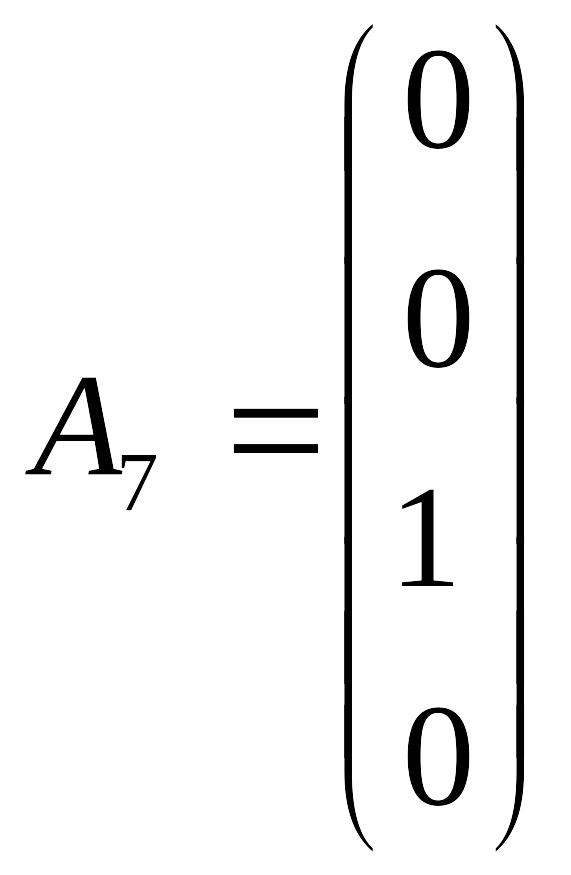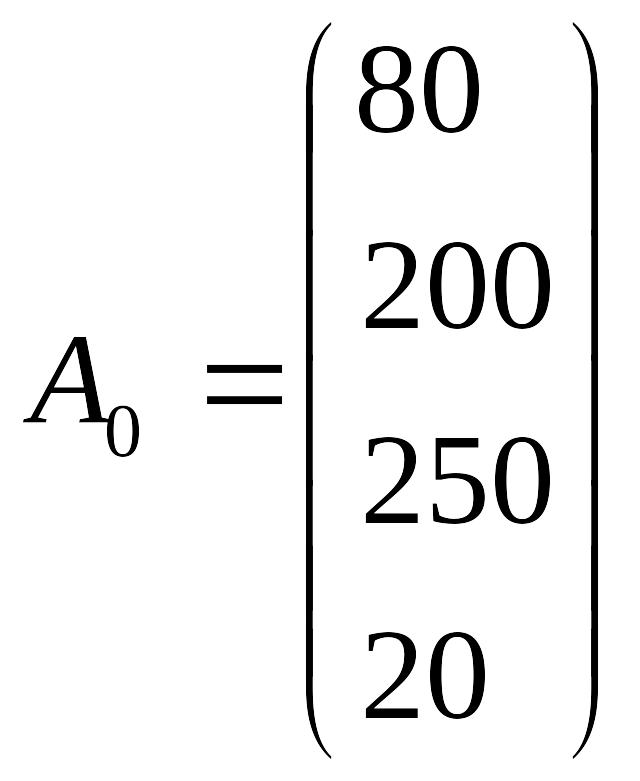
Серед всіх векторів лише два одиничних (А₅ та А₇). В друге та четверте обмеження необхідно ввести штучні змінні. Запишемо обмеження задачі та цільову функцію з штучними змінними:

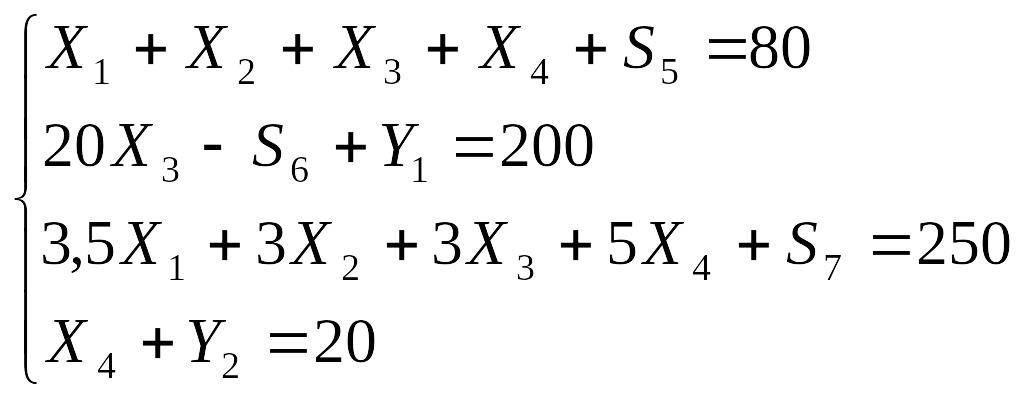
F=160X₁+120X₂+100X₃+260X₄+0S₅+0S₆+0S₇-MY₁-MY₂  max

X – основні змінні, S – додаткові змінні, Y – штучні змінні

Рішення задач симплексним методом здійснюється в таблицях, заповнимо першу таблицю.

Ітерація 1

Базис	C(j)	X1	X2	X3	X4	S1	S2	Y1	S3	Y2	B(i)
		160	120	100	260	0	0	-M	0	-M
S1	0	1	1	1	1	1	0	0	0	0	80	80
Y1	-M	0	0	20	0	0	-1	1	0	0	200	10
S3	0	3,5	3	3	5	0	0	0	1	0	250	83,33
Y2	-M	0	0	0	1	0	0	0	0	1	20	Inf
*Big M		-160 0	-120 0	-100 -20	-260 -1	0 0	0 1	0 0	0 0	0 0	0 -220

Поточне значення цільової функції (Max) = 0+(-220 Big M)

(в базис вводимо змінну Х₃; виводимо змінну Y₁),

Inf – дія не виконується, тому що ділити на 0 неможливо

Система обмежень задачі записується в табличному виді (Ітерація 1): в “Базис” записуються змінні, які утворили систему одиничничних векторів (для першої таблиці), в стовпчик С(j) – коефіцієнти в цільовій функції при змінних, які ввійшли в Базис, в стовпчики Х1, Х2, Х3, Х4, S1, S2, Y1, Y2 – відповідні коефіцієнти при цих змінних в кожному обмеженні; стовпчик B(i) – праві частини рівнянь.

Індексний рядок розраховується за правилом – кожне значення стовпчика С(j) множиться на відповідний елемент розрахункового стовпчика, що отримано в результаті множення додається і з цієї суми віднімається коефіцієнт при змінній в цільовій функції, що отримано: число без М записується в рядок , число з М записується в рядок *Big M.

Наприклад:

розрахуємо індексний рядок для стовпця Х1:

розрахуємо індексний рядок для стовпця Х3:

Задача має оптимальне рішення, коли в індексному рядку не існує від’ємних елементів при рішенні задач на max.

Якщо умова оптимальності не виконується, необхідно визначити генеральний (направляючий) елемент, який лежить на перетині генерального стовпця та генерального рядка, та перейти до нової таблиці. Визначається направляючий стовпець, на який вказує найбільше по абсолютній величині від’ємне значення в індексному рядку. Потім визначається направляючий рядок: необхідно поділити кожне значення стовпця B(i) на відповідне значення генерального стовпця і найменше значення, яке буде отримано, вказуватиме на направляючий рядок. При визначенні генерального рядка неможливо ділити на нуль та від’ємний елемент.

Отже: Х3 – генеральний стовпець;

Рядок 2 – генеральний рядок;

20 – генеральний елемент.

Правила переходу до нової таблиці:

1. Замість генерального елемента записується 1, замість всіх інших елементів генерального стовпця 0;

2. Всі елементи генерального рядка діляться на генеральний елемент;

3. Всі інші елементи таблиці розраховуються за правилом прямокутника:

Якщо з базису виходить деяка штучна змінна, то з цього моменту відповідний стовпець не розраховується.

Розрахуємо другу таблицю (ітерація 2)

Розглянемо як за правилом прямокутника визначається декілька значень:

1) 2)

3) 4)

Ітерація 2

Базис	C(j)	X1	X2	X3	X4	S1	S2	Y1	S3	Y2	B(i)
		160	120	100	260	0	0	-M	0	-M
S1	0	1	1	0	1	1	0,05		0	0	70	70
X3	100	0	0	1	0	0	-0,05		0	0	10	Inf
S3	0	3,5	3	0	5	0	0,15		1	0	220	44
Y2	-M	0	0	0	1	0	0		0	1	20	20
*Big M		-160 0	-120 0	0 0	-260 -1	0 0	5 0		0 0	0 0	1000 -20

Поточне значення цільової функції (Max) =1000+(-20 Big M)

(в базис вводимо змінну Х₄; виводимо змінну Y₂)

Задача ще не має оптимального рішення, слід перейти до нової таблиці (ітерація 3).

Ітерація 3

Базис	C(j)	X1	X2	X3	X4	S1	S2	Y2	S3	Y4	B(i)
		160	120	100	260	0	0	-M	0	-M
S1	0	1	1	0	0	1	0,05		0		50	50
X3	100	0	0	1	0	0	-0,05		0		10	Inf
S3	0	3,5	3	0	0	0	0,15		1		120	34,29
X4	260	0	0	0	1	0	0		0		20	Inf
		-160	-120	0	0	0	-5		0		6200

Поточне значення цільової функції (Max) =6200

(в базис вводимо змінну Х₁; виводимо змінну S₃)

Ітерація 4

Базис	C(j)	X1	X2	X3	X4	S1	S2	Y2	S3	Y4	B(i)
		160	120	100	260	0	0	-M	0	-M
S1	0	0	0,143	0	0	1	0,007		-0,286		15,71	0
X3	100	0	0	1	0	0	-0,05		0		10	0
X1	160	1	0,857	0	0	0	0,043		0,286		34,29	0
X4	260	0	0	0	1	0	0		0		20	0
		0	17,1	0	0	0	1,86		45,7		11685,7

(Max) Оптимальна величина ЦФ=11685,7

Задача має оптимальне рішення, так як в індексному рядку не існує від’ємних елементів (виконується умова оптимальності).

Щоб фермеру отримати максимальний прибуток в розмірі 11685,7 грн., необхідно посіяти 34,29 га пшениці (Х₁), 10 га проса (Х₃), 20 га картоплі (Х₄).

При такому плані виробництва залишається незасіяна рілля в кількості 15,71га (S₁); добрива та трудові ресурси будуть використані повністю (в стовпчику „Базис” нема змінних S₂ та S₃).