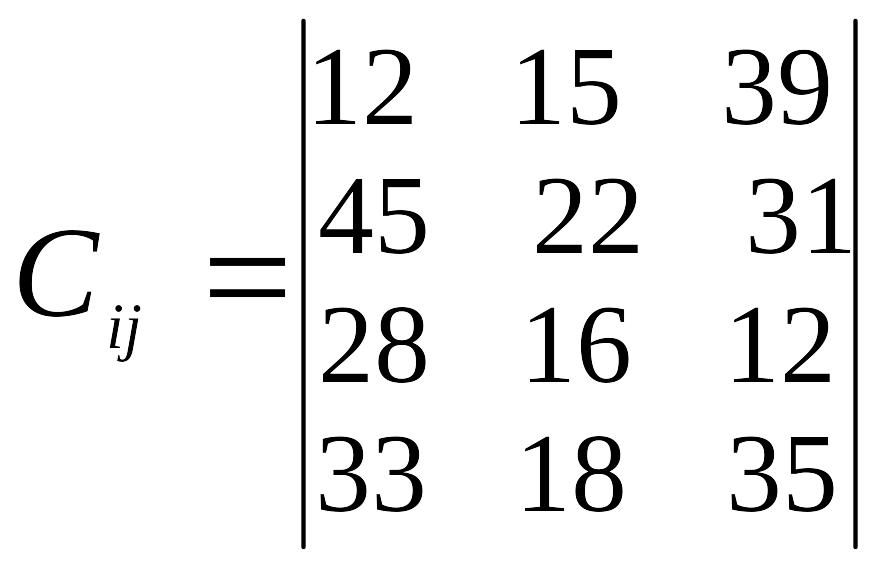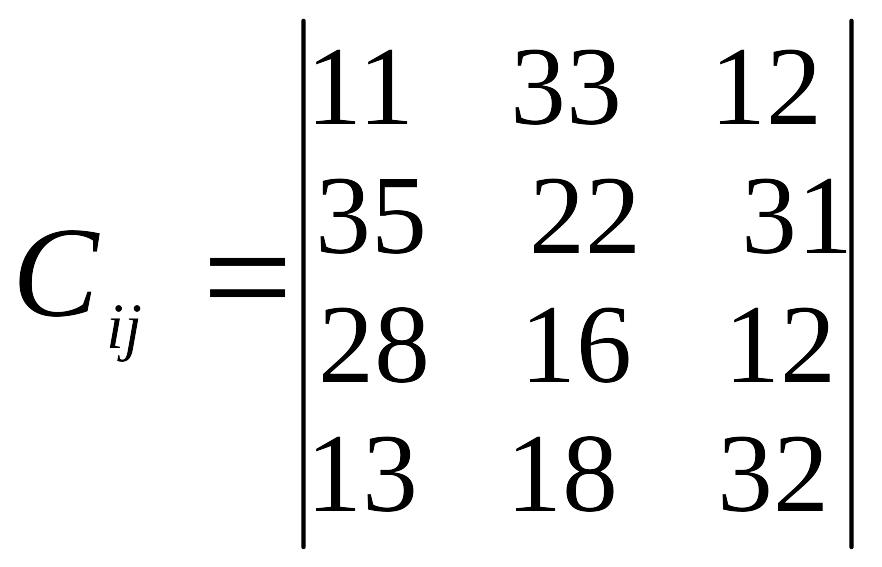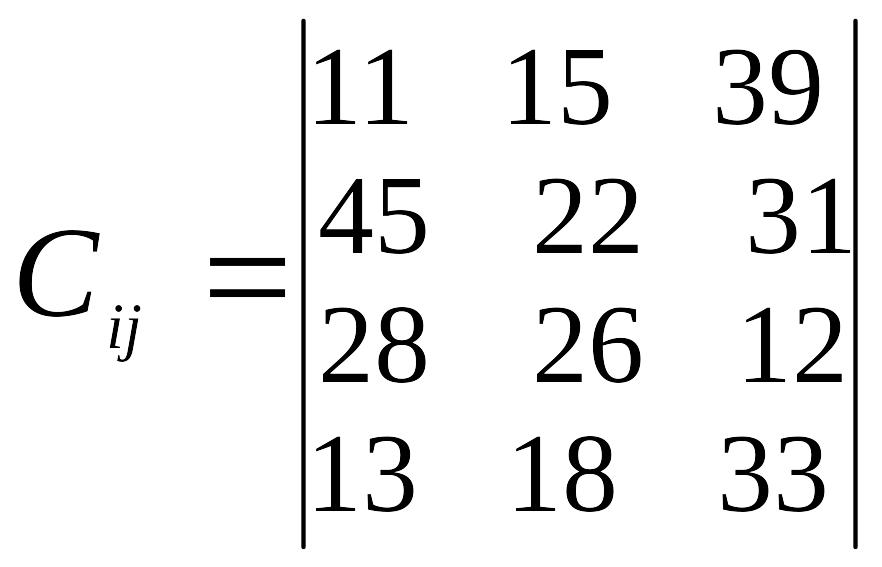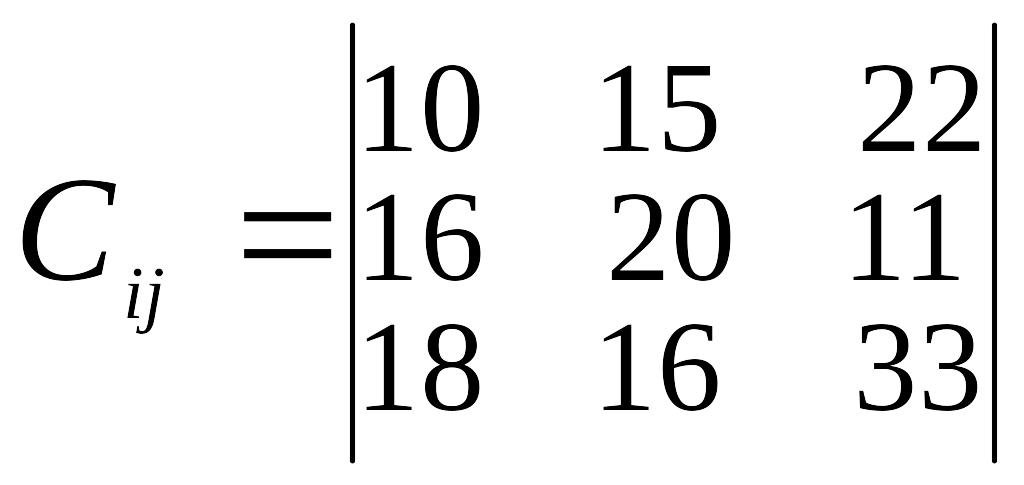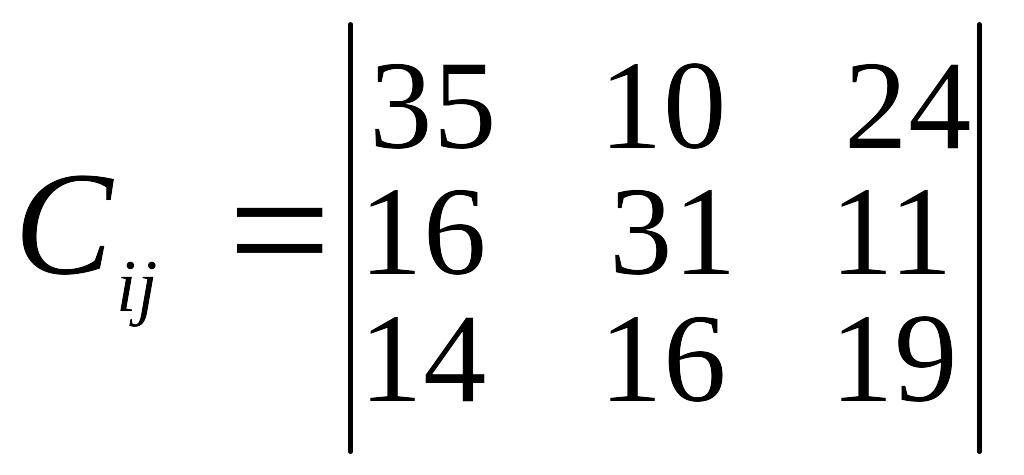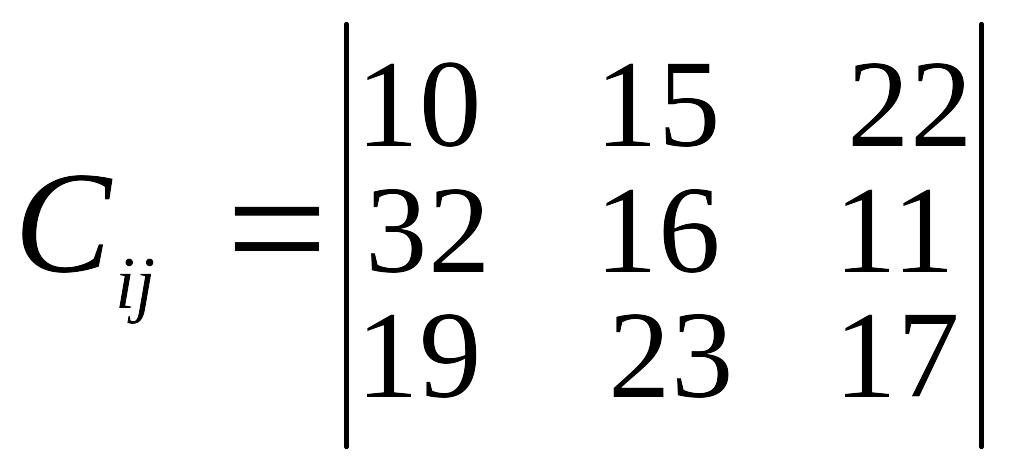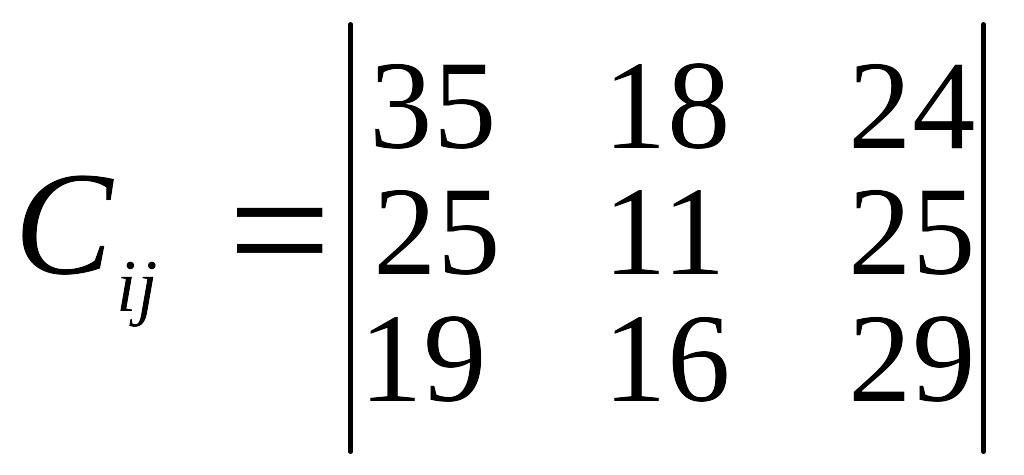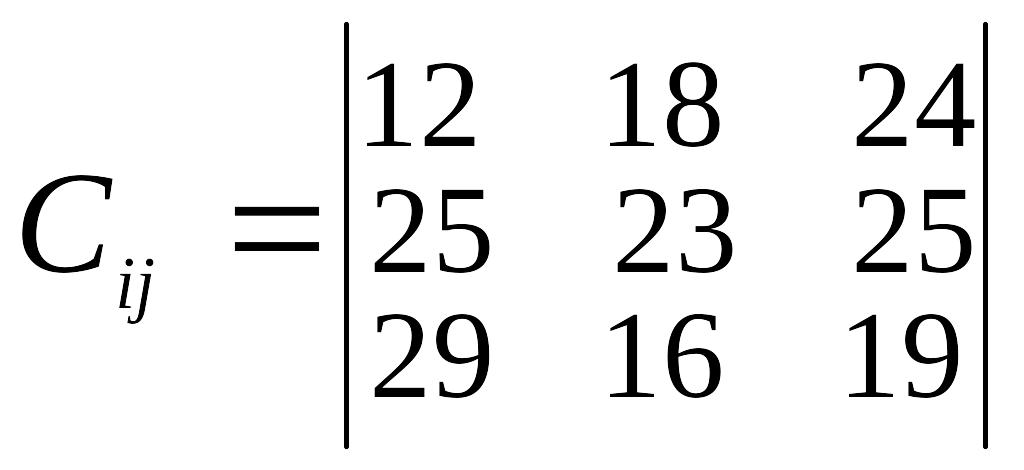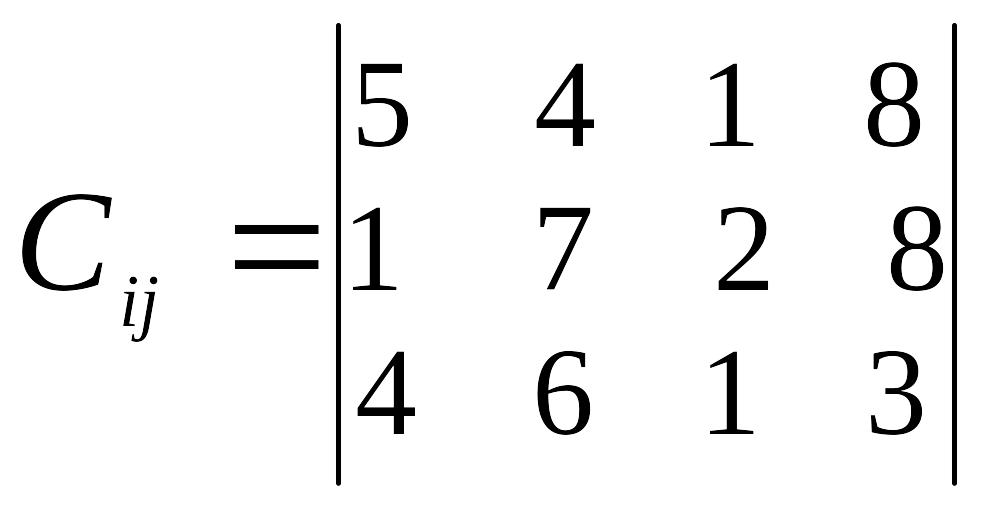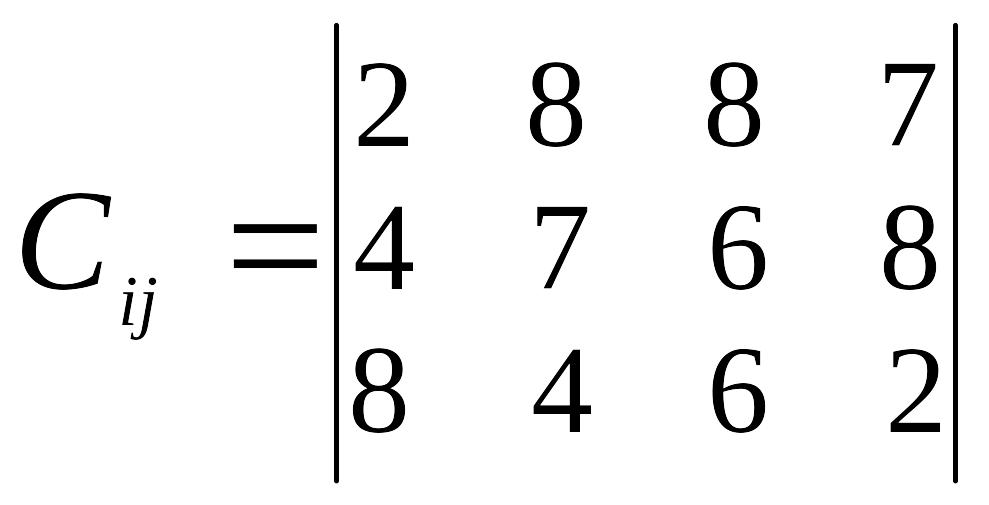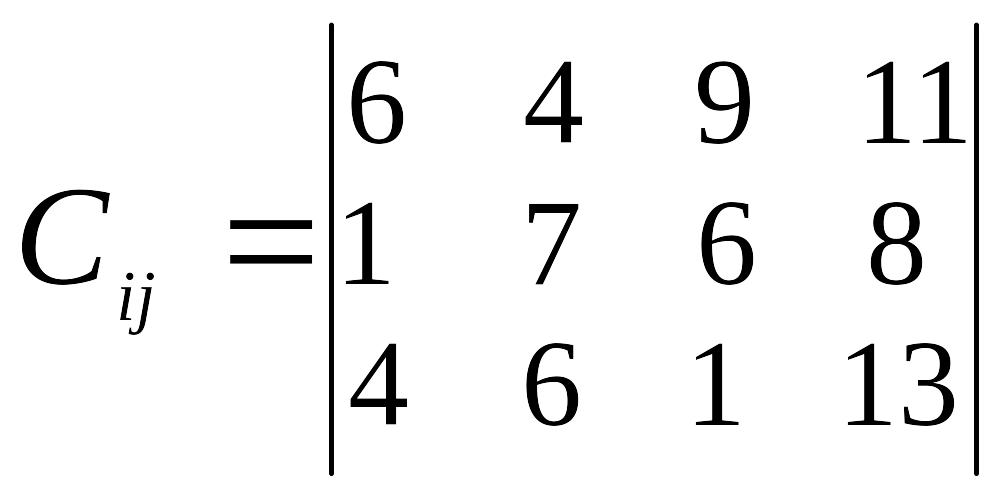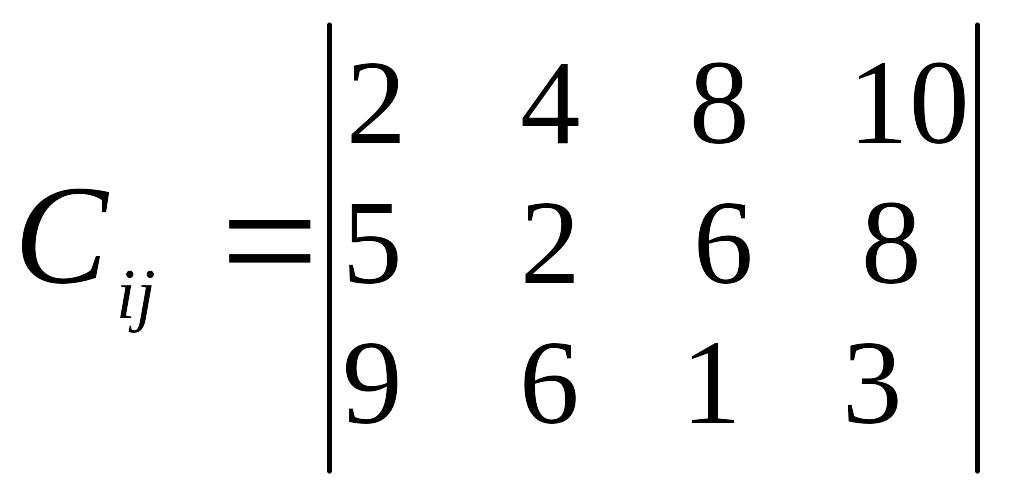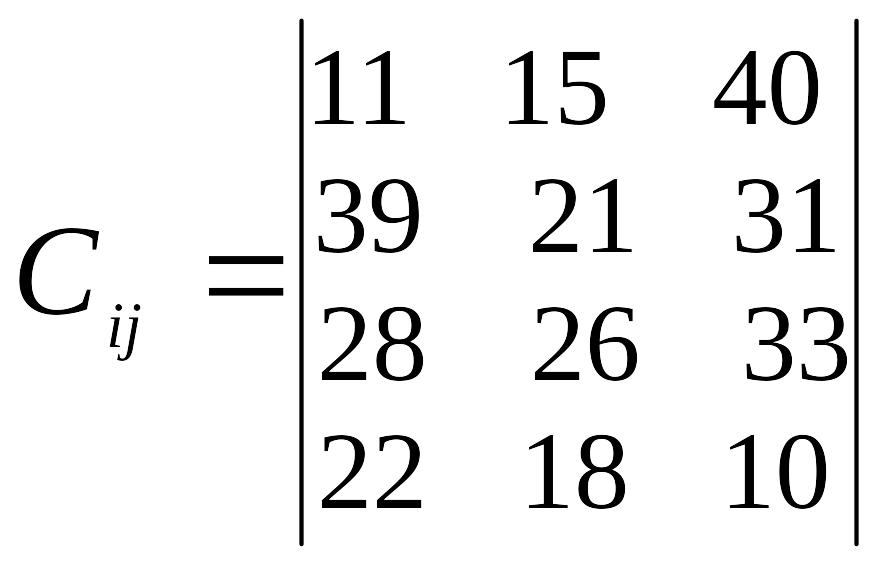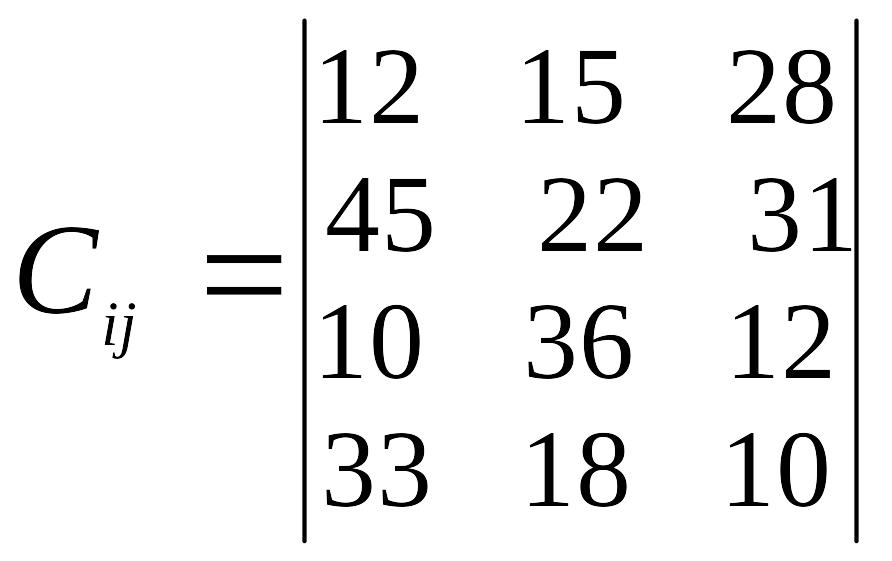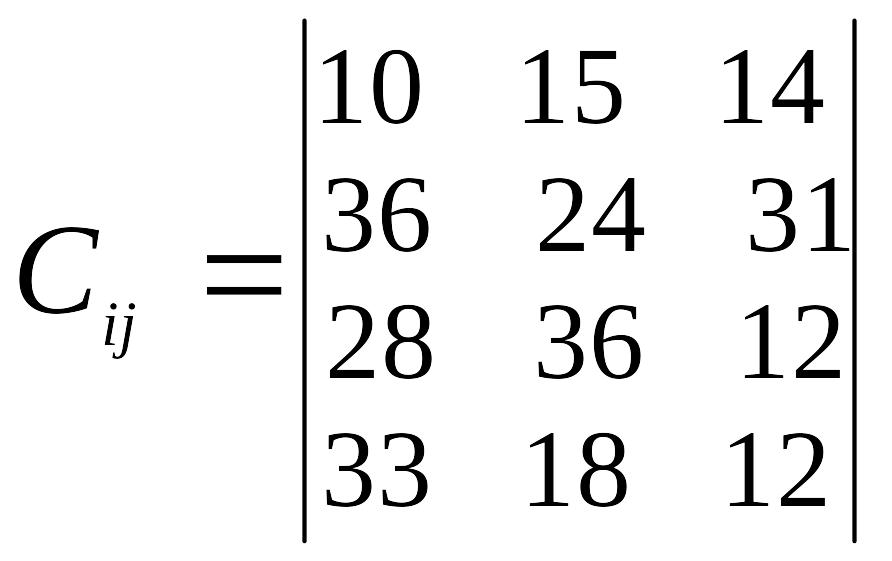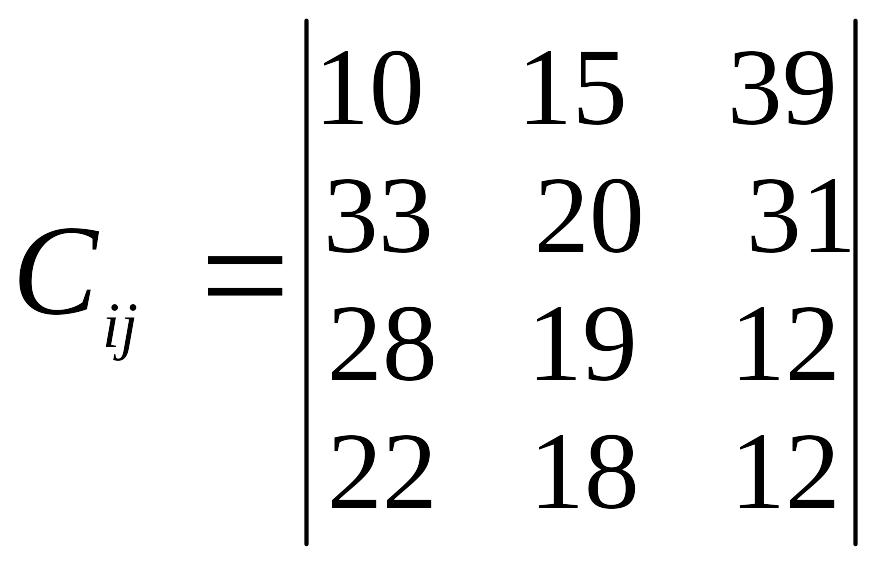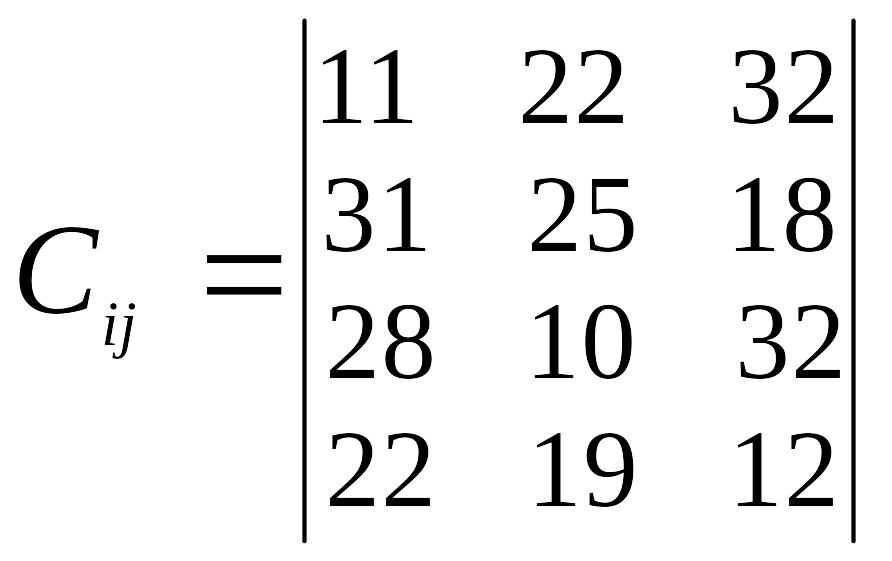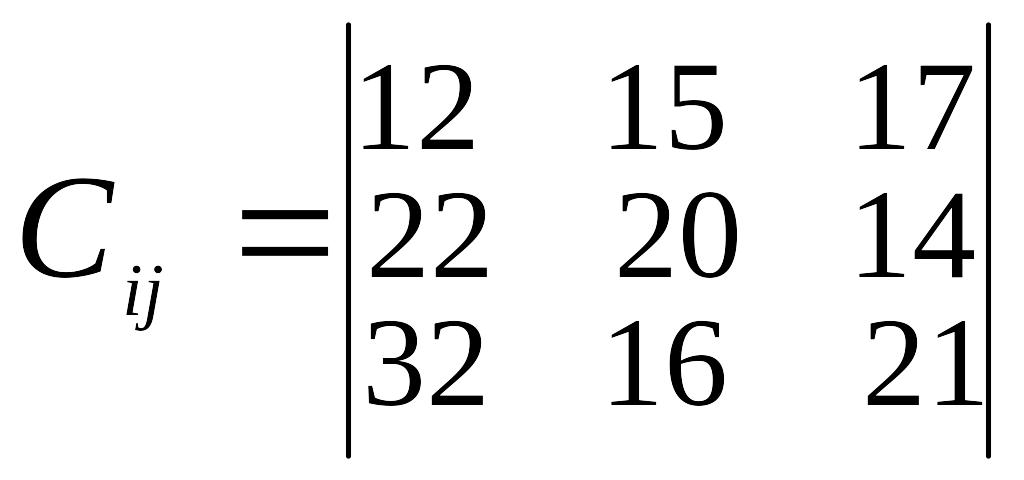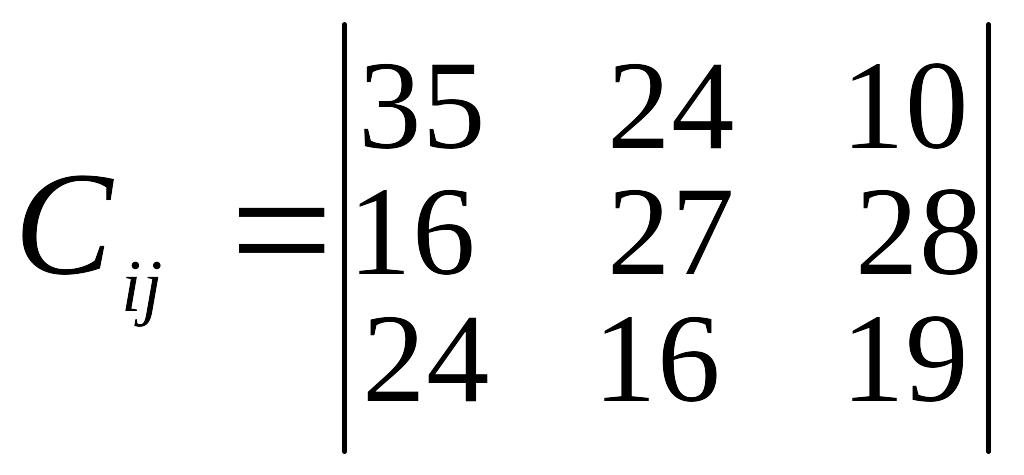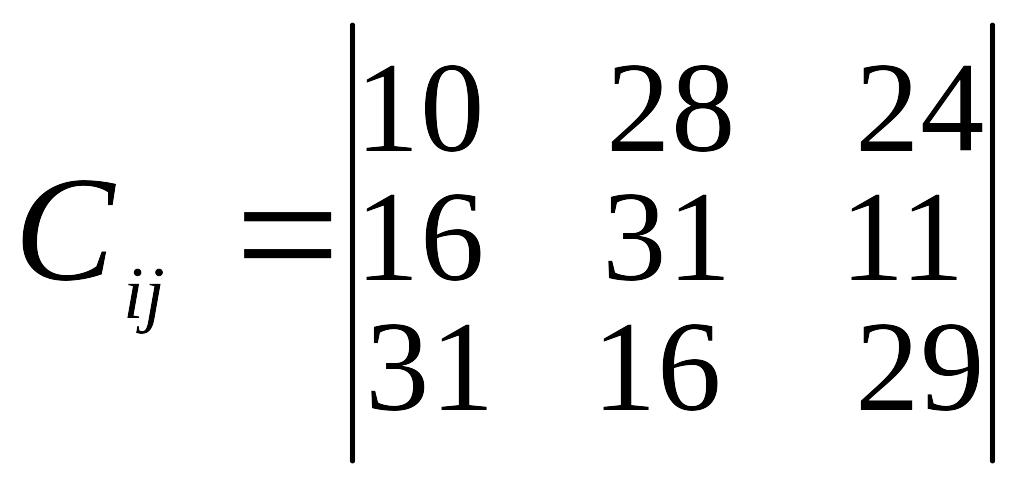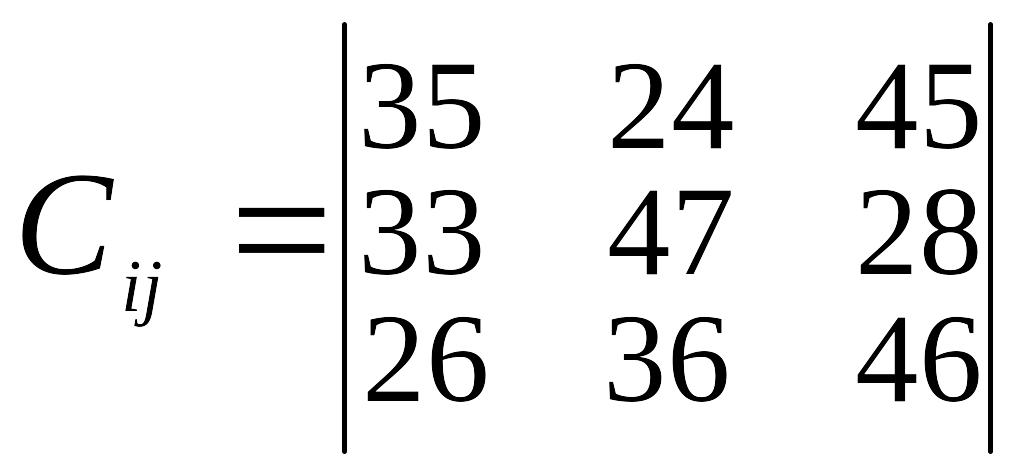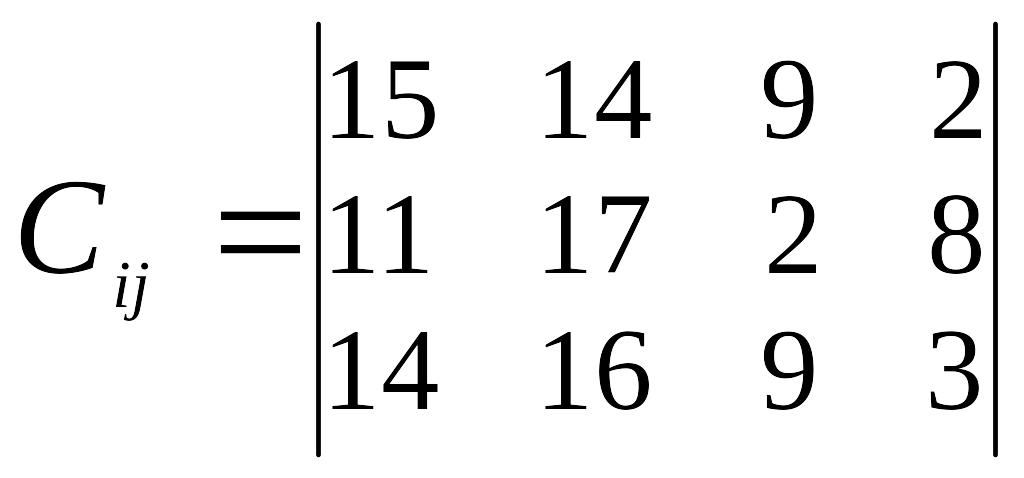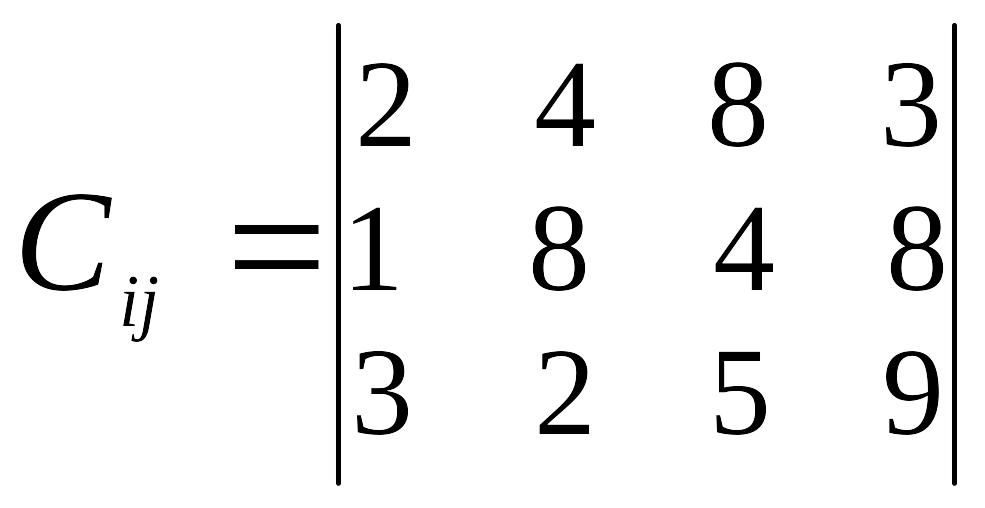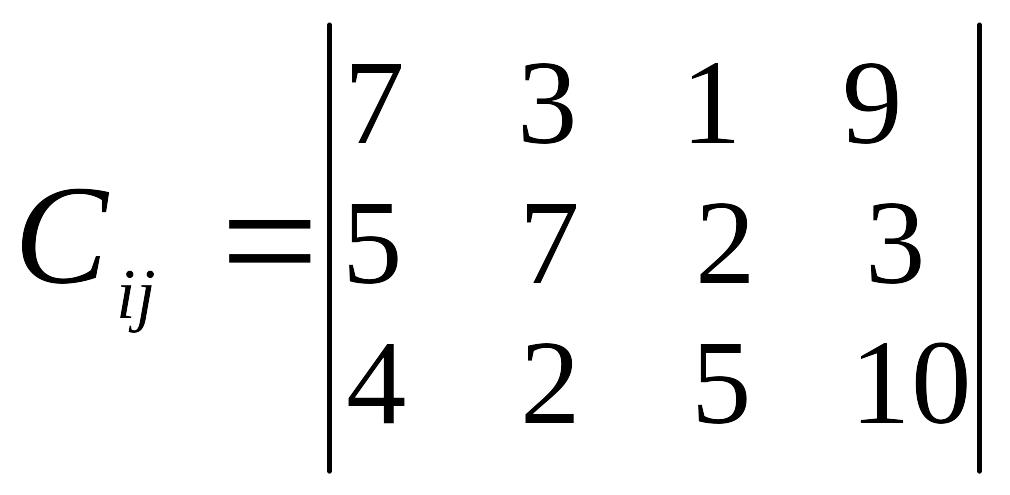- •Тема 1. Робочий зошит 3
- •Передмова
- •Робочий зошит
- •1. Вирішення економіко-математичних задач методами лінійного програмування
- •1.1. Симплексний метод
- •1.2. Метод потенціалів
- •Аналіз рішення
- •2. Економіко-математичні моделі для розрахунку оптимальних планів розвитку рослинництва
- •2.1. Економіко-математична модель оптимізації структури посівних площ
- •Розподіл продукції рослинництва і вихід живильних речовин
- •2.2. Економіко-математична модель оптимізації розподілу мінеральних добрив
- •Тема 2. Основні задачі статистичного моделювання Основна література.
- •Умова задачі.
- •2. Нормативні рівні чинників та результативного показника:
- •Варіанти задачі
- •Приклад виконання задачі.
- •1. Умова задачі.
- •2. Приклад рішення задачі.
- •2.2. Визначити нормативні розрахунки рівнів чинників та результативного показника
- •Нормативні розрахунки
- •Тема 3. Задачі лінійного програмування і їх застосування в управлінні сільськогосподарським виробництвом
- •1. Загальні рекомендації
- •2. Теоретичні питання
- •Задача 2
- •Загальна характеристика симплексного методу.
- •Алгоритм симплексного методу
- •Умова задачі.
- •Задача 3 Транспортна задача лінійного програмування. Загальна постановка задачі.
- •Умова задачі.
- •Задача 4. Економіко-математична модель оптимізації структури посівних площ. Загальна постановка задачі.
- •Умова задачі.
- •Рішення.
- •Задача 2. Симплексний метод розв’язання задач лінійного програмування. Умова задачі.
- •Рішення
- •Задача 3. Розв’язання транспортної задачі лінійного програмування. Умова задачі.
- •Рішення.
- •Задача 4. Економіко-математична модель оптимізації структури посівних площ. Умова задачі.
- •Рішення.
- •Задача 5 Економіко-математична модель оптимізації виробничої структури садового агропромислового підприємства
- •2. Початкова інформація
- •3. Система змінних моделі
- •Система обмежень моделі
- •Множини:
- •Шукані змінні:
- •Техніко-економічні коефіцієнти при змінних і вільні члени:
- •По технологічним взаємостосункам:
- •5. Аналіз оптимального рішення
- •Варіанти завдань для складання економіко-математичної моделі оптимізації виробничої структури агропромислового підприємства
- •Тема 4. Теорія ігор
- •2. Завдання 1.
- •Тема 5. Використання теорії графів.
- •Тема 6. Поняття про експертні системи експертні системи «корал»
- •1. Мета заняття
- •2. Зміст теми
- •Область Експерта
- •Область Користувача
- •3. Завдання
- •Термінологічний словник.
- •7. Література
- •Типова программа дисципліни «Моделювання технологічних процесів і систем» для студентів напряму підготовки 6.090101 “Агрономія” передмова
- •Теоретичні заняття
- •Список рекомендованої літератури
- •Економіко-математична модель оптимізації виробничої структури господарства.
- •Рішення завдань лінійного програмування за допомогою Excel Блок-схема рішення задачі
- •3.3.2. Введення умов задачі
- •Алгоритм 3.3.1. Уведення даних для рішення задачі лінійного програмування
- •Алгоритм 3.3.2. Робота в діалоговому вікні Пошук рішення
- •1. Сервіс, Пошук рішення...
- •4. Додати...
- •3.3.3. Рішення задачі
- •Алгоритм 3.3.3. Рішення задачі лінійного програмування
- •1. Параметри...
- •Максимальний час
- •Граничне число ітерацій
- •4. Виконати.
- •3.3.4. Графічне представлення результатів рішення
- •3.3.5. Подолання несумісності
- •Алгоритм 3.3.4. Зміна умов задачі
- •Алгоритм 3.3.5. Подолання несумісності
- •2. Сервіс, Пошук рішення...
- •6. Виконати.
- •3.3.6. Усунення необмеженості цільової функції
- •Моделювання в апк
- •Частина 2. Моделювання технологічних процесів
- •І систем. Практикум.
- •Навчальний посібник
Умова задачі.
В пунктах відправлення А1, А2, А3, .... знаходиться однорідний вантаж в кількості a1, а2, а3, .... відповідно, який необхідно перевезти в пункти призначення В1, В2, В3, .... , потреба кожного з яких становить b1, b2, b3, .... . Відома відстань між пунктами перевезень (оцінки).
Визначити такий план перевезень, при якому загальна кількість тоно-кілометрів буде мінімальною.
Вихідні дані згідно варіанту наведені в таблиці 3.
Вказівка: Скласти відповідну задачу математичного програмування, привести її до закритого типу та розв’язати методом потенціалів.
Таблиця 3
Варіант |
Відстань між пунктами перевезень, км |
Запаси пунктів відправлення, т |
Потреба пунктів призначення, т |
1 |
|
а1=6 а2=8 а3=5 а4=6 |
в1=9 в2=8 в3=4 |
2 |
|
а1=60 а2=85 а3=52 а4=66 |
в1=92 в2=81 в3=43 |
3 |
|
а1=26 а2=28 а3=25 а4=26 |
в1=29 в2=28 в3=34 |
4 |
|
а1=56 а2=58 а3=55 а4=56 |
в1=69 в2=68 в3=44 |
5 |
|
а1=16 а2=18 а3=15 а4=16 |
в1=19 в2=18 в3=14 |
6 |
|
а1=50 а2=85 а3=52 |
в1=62 в2=81 в3=43 |
7 |
|
а1=45 а2=43 а3=42 |
в1=42 в2=40 в3=44 |
8 |
|
а1=15 а2=18 а3=15 |
в1=20 в2=18 в3=10 |
9 |
|
а1=25 а2=33 а3=22 |
в1=32 в2=20 в3=24 |
10 |
|
а1=25 а2=31 а3=27 |
в1=33 в2=20 в3=34 |
11 |
|
а1=25 а2=33 а3=32 |
в1=32 в2=20 в3=24 в4=14 |
12 |
|
а1=55 а2=63 а3=72 |
в1=32 в2=60 в3=54 в4=54 |
13 |
|
а1=15 а2=13 а3=12 |
в1=12 в2=10 в3=14 в4=54 |
14 |
|
а1=25 а2=33 а3=33 |
в1=12 в2=10 в3=24 в4=24 |
15 |
|
а1=53 а2=40 а3=35 |
в1=33 в2=30 в3=31 в4=34 |
16 |
|
а1=2 а2=8 а3=4 а4=6 |
в1=7 в2=8 в3=4 |
17 |
|
а1=16 а2=11 а3=15 а4=16 |
в1=19 в2=18 в3=24 |
18 |
|
а1=7 а2=8 а3=3 а4=6 |
в1=8 в2=8 в3=7 |
19 |
|
а1=60 а2=85 а3=52 а4=66 |
в1=22 в2=21 в3=33 |
20 |
|
а1=10 а2=15 а3=12 а4=6 |
в1=12 в2=31 в3=33 |
21 |
|
а1=46 а2=33 а3=22 |
в1=55 в2=22 в3=24 |
22 |
|
а1=5 а2=8 а3=5 |
в1=6 в2=8 в3=4 |
23 |
|
а1=25 а2=33 а3=22 |
в1=32 в2=20 в3=24 |
24 |
|
а1=44 а2=33 а3=22 |
в1=55 в2=20 в3=24 |
25 |
|
а1=15 а2=13 а3=12 |
в1=12 в2=10 в3=14 |
26 |
|
а1=25 а2=25 а3=32 |
в1=12 в2=20 в3=13 в4=14 |
27 |
|
а1=5 а2=3 а3=7 |
в1=3 в2=6 в3=4 в4=5 |
28 |
|
а1=25 а2=33 а3=32 |
в1=32 в2=20 в3=24 в4=14 |
29 |
|
а1=75 а2=73 а3=73 |
в1=62 в2=40 в3=54 в4=54 |
30 |
|
а1=5 а2=3 а3=9 |
в1=2 в2=1 в3=4 в4=6 |