0

МІНІСТЕРСТВО АГРАРНОЇ ПОЛІТИКИ та продовольства

УКРАЇНИ

СУМСЬКИЙ НАЦІОНАЛЬНИЙ АГРАРНИЙ УНІВЕРСИТЕТ

МОДЕЛЮВАННЯ В АПК

Частина 2. Моделювання технологічних процесів

і систем. Практикум.

Навчальний посібник

Суми 2012

МІНІСТЕРСТВО АГРАРНОЇ ПОЛІТИКИ УКРАЇНИ

СУМСЬКИЙ НАЦІОНАЛЬНИЙ АГРАРНИЙ УНІВЕРСИТЕТ

Кафедра кібернетики та інформатики

МОДЕЛЮВАННЯ В АПК

Частина 2. Моделювання технологічних процесів

і систем. Практикум.

Навчальний посібник

для студентів 5 курсу напряму підготовки 6.090101

“Агрономія”

денної та заочної форм навчання

Суми 2012

УДК 681.3: 519.6 (073)

Укладач: В’юненко О.Б., доцент кафедри кібернетики та інформатики СНАУ

Моделювання в АПК. Частина 2. Моделювання технологічних процесів і систем. Практикум. Навчальний посібник для студентів 5 курсу напряму підготовки 6.090101 “Агрономія” денної та заочної форм навчання / Суми, 2012 рік, 192 ст., табл. 83, рис. 37, бібл. 53.

Навчальний посібник призначений для надання методичної допомоги студентам під час вивчення теми курсу “Моделювання технологічних процесів і систем”, а також виконання студентами практичних робіт. Посібник містить загальні теоретичні питання, методичні рекомендації, варіанти та приклади виконання задач.

Рецензенти:	Ободяк В.К. к.т.н., доцент кафедри комп’ютерних наук Сумського державного університету
	Герасименко В.О., к.фіз.-мат.н., доцент кафедри вищої математики Сумського національного аграрного університету

Відповідальний за випуск: Смоляров Г.А., доцент кафедри кібернетики та інформатики СНАУ

Розглянуто навчально-методичною комісією інституту економіки та менеджменту

Протокол №5 від 10.05.12 р.

Рекомендовано до видання методичною радою Сумського національного аграрного університету. Протокол № __ від “___” _________ 2012 року.

 Сумський національний аграрний університет, 2012

Зміст

стор.

Передмова 3

Тема 1. Робочий зошит 3

1. Вирішення економіко-математичних задач методами

лінійного програмування 4

1.1. Симплексний метод 4

1.2. Метод потенціалів 12

2. Економіко-математичні моделі для розрахунку оптимальних планів розвитку рослинництва 18

2.1. Економіко-математична модель оптимізації структури посівних площ18

2.2. Економіко-математична модель оптимізації розподілу мінеральних добрив 30

Тема 2. Основні задачі статистичного моделювання 38

Тема 3. Задачі лінійного програмування і їх застосування в управлінні сільськогосподарським виробництвом 58

Тема 4. Теорія ігор 132

Тема 5. Використання теорії графів 138

Тема 6. Поняття про експертні системи 139

6. Термінологічний словник 148

7. Література 153

Додаток 1. Типова програма дисципліни 158

Додаток 2. Економіко-математична модель оптимізації виробничої структури господарства. 163

Додаток 3. Рішення завдань лінійного програмування за допомогою табличного процесора Excel 175

Передмова

Для забезпечення розвитку та інтенсифікації сільського господарства необхідно широко впроваджувати сучасні досягнення науки і техніки. З метою обґрунтованого та швидкого прийняття оптимальних рішень, фахівці в галузі сільського господарства мають володіти сучасними методами моделювання технологічних процесів та виконувати достатньо складні розрахункові роботи, які без застосування обчислювальних засобів реалізувати важко.

Навчальний посібник підготовлено відповідно до програми курсу «Моделювання технологічних процесів і систем», посібник розрахований на студентів, які навчаються за програмами підготовки магістрів технологічних фахових спрямувань (Додаток 1). При підготовці посібника використано матеріал робіт, присвячених проблемам побудови систем оптимізації технологічних процесів, робота не ставила за мету викладання власних наукових результатів, навчальний посібник створений, виходячи з актуальності питань електронної комерції та великої проблеми самостійного опанування матеріалом через нестачу літератури, на базі існуючих напрацювань [6-8, 12, 13, 16-23].

Робочий зошит

Робочий зошит складено відповідно до програми курсу і складається з двох розділів. У першому приводяться дві спрощені економіко-математичні завдання, що вирішуються методами лінійного програмування: перша — симплексним методом, друга — методом потенціалів. У другому розділі даються два завдання по складанню економіко-математичних моделей для розрахунку оптимальних планів розвитку рослинництва: оптимізації структури посівних площ і розподілу мінеральних добрив.

Після вказівок слідують схеми рішення кожної задачі і аналізи результатів рішень. Студенти відповідно до схем виконують тільки розрахункову частину роботи, що значно скорочує час на виконання завдань, частину яких вони повинні виконувати самостійно [22].

1. Вирішення економіко-математичних задач методами лінійного програмування

1.1. Симплексний метод

Завдання. Потрібно знайти оптимальне поєднання посівів трьох продовольчих культур: озимої іржі, озимої пшениці і картоплі. Під посіви відведено 1000га ріллі, яка повинна використовуватися повністю. При цьому загальні ресурси праці складають 30000 людино-годин.

Виробництво культур характеризується наступними показниками (табл. 1).

Таблиця 1

Показники	Озиме жито	Озима пшениця	Картопля
Врожайність з 1га, ц	32	40	250
Витрати праці на 1га, люд.-год.	16	20	80
Матеріально-грошові витрати на 1га, у.о.	214-	226	782

За планом потрібно провести 32000ц зерна і 40000ц картоплі.

Критерій оптимальності — мінімум матеріально-грошових витрат на виробництво продукції.

Вказівки до виконання завдання. Дане завдання може бути вирішена за допомогою симплексного методу лінійного програмування. Для цього необхідно слідувати певним правилам.

Перш за все, невідомі завдання позначаються через хj, всі умови виражаються у вигляді лінійних обмежень і записується цільова функція Z, тобто складається економіко-математична модель.

Потім проводиться ряд перетворень:

1) Всі нерівності приводяться до рівності. Для цього в ліву частину обмежень типу «<» вводяться додаткові змінні з коефіцієнтами «+1», а типу «=» — -с коефіцієнтами «—1». У цільову функцію додаткові змінні вводяться з нульовою оцінкою. При цьому необхідно пояснити економічний сенс додаткових змінних.

2) У ліву частину обмежень, в яких немає додаткових змінних з коефіцієнтами «+1>, вводяться штучні змінні yj з коефіцієнтами «+1». У цільову функцію штучні змінні вводяться з дуже великою позитивною оцінкою «М», якщо завдання вирішується на мінімум, і з «— М» при рішенні на максимум.

3) Всі обмеження вирішуються щодо додаткових або штучних змінних з коефіцієнтами «+1». Відповідним чином перетвориться цільова функція. При цьому вона для зручності записується двома рядками. У перший цільовий рядок Z записуються оцінки при основних і додаткових змінних із зворотним знаком. У другий цільовий рядок F записуються оцінки, отримані шляхом множення рівнянь, що містять штучні змінні, на оцінки «М» або «— М» залежно від рішення задачі, відповідно, па мінімум або максимум і подальшим їх підсумовуванням.

Після цього заповнюється перша симплексна таблиця, в неї записується перший опорний план, який, як правило, не є оптимальним. Потім за допомогою алгоритму симплексного методу проводиться поліпшення першого опорного плану і заповнюється нова симплексна таблиця.

Алгоритм симплексного методу (рішення задачі на мінімум в скорочених симплексних таблицях).

1. Вибирається вирішуючий стовпець j* за максимальною додатної при рішенні на максимум — по максимальній по абсолютній від’ємної величині) оцінкою в рядку F. Якщо в рядку F немає додатних (при рішенні на максимум — від’ємних) оцінок, то стовпець вибирається аналогічно по оцінках рядка Z, виключаючи стовпці, в яких в рядку F коштують від’ємні (при рішенні на максимум — додатні) оцінки. План вважається оптимальним в тому випадку, якщо не можна знайти вирішуючий стовпець.

2. Вибирається вирішуючий рядок i* по мінімальному частка від ділення елементів стовпця вільних членів b_і на додатні елементи вирішуючого стовпця a_ij . Якщо у вирішуючому стовпці немає додатних елементів, то завдання не має рішення. На перетині вирішуючого стовпця і вирішуючого рядка стоїть вирішуючий елемент.

Для наочності і зручності подальших обчислень вирішуючий стовпець і рядок виділяються жирними лініями.

3. Заповнюється нова таблиця.

3.1. Змінна, що стоїть у вирішуючому рядку, виводиться з базису, а змінна, що стоїть у вирішуючому стовпці, вводиться в базис, тобто дані змінні міняються місцями. Решта змінних залишається на своїх місцях.

3.2. Замість вирішуючого елементу записується його зворотна величина

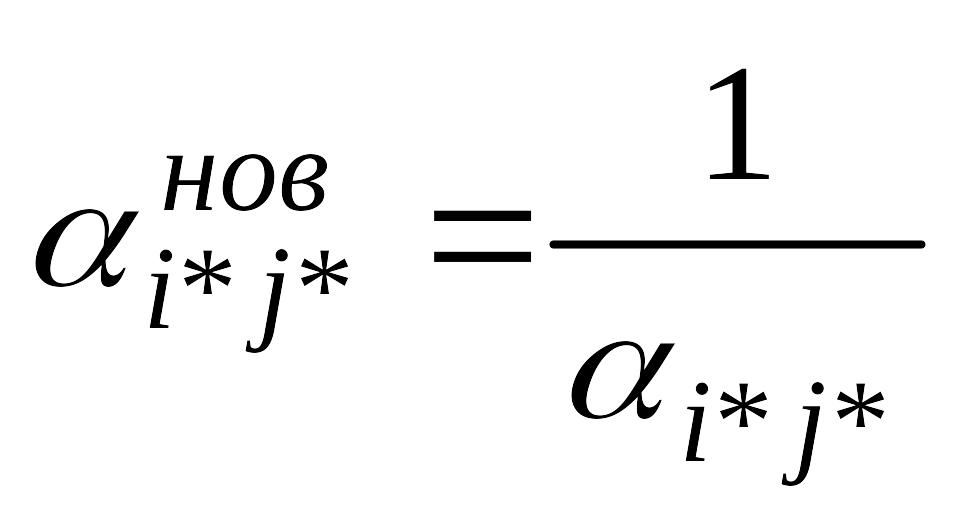
3.3. Заповнюється початковий рядок нової таблиці, що стоїть на місці вирішуючого. Для цього елементи вирішуючого рядка діляться на вирішуючий елемент

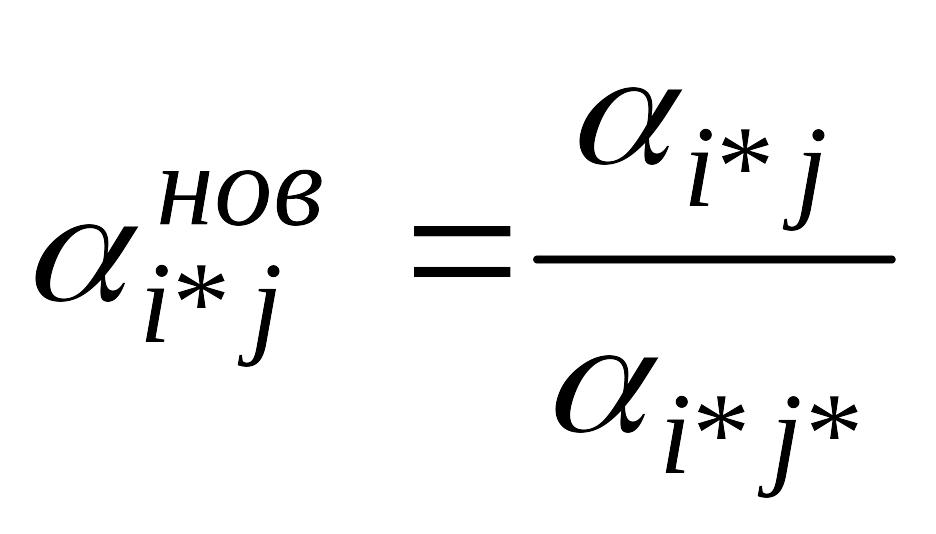
3.4. Заповнюється стовпець нової таблиці, що стоїть на місці вирішуючого. Для цього елементи вирішуючого стовпця діляться на вирішуючий елемент, узятий із зворотним знаком

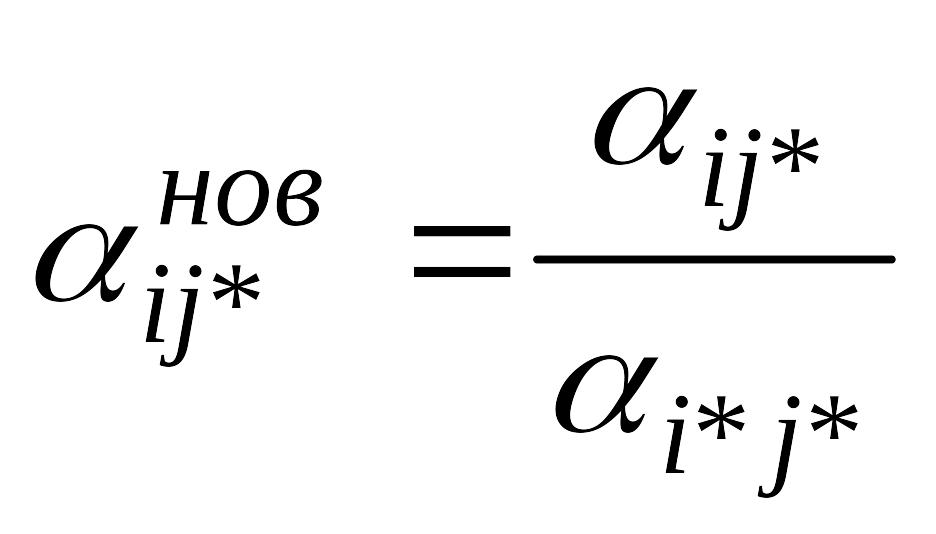
3.5. Решта елементів нової таблиці розраховується по формулі:

або

4. Йти до 1.

Після отримання оптимального плану проводиться аналіз і перевірка рішення.

Перевірка здійснюється шляхом підстановки значень базисних змінних в початкову систему обмежень.

Рішення задачі. Позначимо через:

х₁ – площа під озиму рож

х₂ – площа під озиму пшеницю

х₃ – площа під картоплю

Запишемо умови завдання у вигляді системи обмежень:

1) 32х₁+40х₂≥32000

2) 250х₃≥40000

3) 16х₁+20х₂+80х₃≤30000

4) х₁+х₂+х₃=1000

Цільова функція – Z=214x₁+226x₂+782x₃min

Перейдемо в системі обмежень від нерівності до рівності. Для цього введемо додаткові змінні:

1)

2)

3)

4)

Z=

Додаткові змінні мають наступний економічний сенс:

х₄ - надлишок зернових

х₅ – надлишок картоплі

х₆ – надлишок трудових ресурсів

У обмеження, в яких немає додаткових змінних з коефіцієнтом «+1», введемо штучні змінні. У цільову функцію введемо їх з оцінками «М», оскільки завдання вирішується на мінімум:

1) y₁

2) y₂

3) y₃

4)

Z=0-(-214x₁-226x₂-782x₃)

Вирішимо рівняння щодо штучних змінних з коефіцієнтами «+1». Аналогічно запишемо цільову функцію, представивши її для зручності двома рядками:

1)

2)

3)

4)

Z =

F=

Складемо першу симплексну таблицю.

Симплексна таблиця 1

i	Базисні змінні	Вільні члени, b1	x1	x2	x3	x4	x5	x6
1	y1	32000	32	40	0	-1	0	0
2	y2	40000	0	0	250	0	-1	0
3	x6	30000	16	20	80	0	0	6
4	y3	1000	1	1	1	0	0	0
m+1	Z	0	-240	-220	-782	0	0	0
m+2	F

1. Вирішуючий стовпець

2. Вирішуючий рядок

3. Заповнюється симплексна табл. 2.

3.1. Змінна___ виводиться з базису, змінна __ вводиться в базис.

3.2. Розрахунок елементу, що стоїть на місці вирішуємого:

3.3. Розрахунок елементів початкового рядка, що стоїть на місці вирішуємого:

3.4. Розрахунок елементів стовпця, що стоїть на місці вирішує мого:

3.5. Розрахунок решти елементів таблиці:

Симплексна таблиця 2.

i	Базисні змінні	Вільні члени, b1
1
2
3
4
m+1	Z
m+2	F

1. Вирішуючий стовпець

2. Вирішуючий рядок

3. Заповнюється симплексна табл. 3.

3.1. Змінна___ виводиться з базису, змінна __ вводиться в базис.

3.2. Розрахунок елементу, що стоїть на місці вирішуємого:

3.3. Розрахунок елементів початкового рядка, що стоїть на місці вирішуємого:

3.4. Розрахунок елементів стовпця, що стоїть на місці вирішує мого:

3.5. Розрахунок решти елементів таблиці:

Симплексна таблиця 3.

i	Базисні змінні	Вільні члени, b1
1
2
3
4
m+1	Z
m+2	F

1. Вирішуючий стовпець

2. Вирішуючий рядок

3. Заповнюється симплексна табл. 4.

3.1. Змінна___ виводиться з базису, змінна __ вводиться в базис.

3.2. Розрахунок елементу, що стоїть на місці вирішуємого:

3.3. Розрахунок елементів початкового рядка, що стоїть на місці вирішуємого:

3.4. Розрахунок елементів стовпця, що стоїть на місці вирішує мого:

3.5. Розрахунок решти елементів таблиці:

Симплексна таблиця 4.

i	Базисні змінні	Вільні члени, b1
1
2
3
4
m+1	Z
m+2	F

1. Вирішуючий стовпець

2. Вирішуючий рядок

3. Заповнюється симплексна табл. 5.

3.1. Змінна___ виводиться з базису, змінна __ вводиться в базис.

3.2. Розрахунок елементу, що стоїть на місці вирішуємого:

3.3. Розрахунок елементів початкового рядка, що стоїть на місці вирішуємого:

3.4. Розрахунок елементів стовпця, що стоїть на місці вирішує мого:

3.5. Розрахунок решти елементів таблиці:

Симплексна таблиця 5.

i	Базисні змінні	Вільні члени, b1
1
2
3
4
m+1	Z
m+2	F

1. Вирішуючий стовпець

2. Вирішуючий рядок

3.1. Змінна___ виводиться з базису, змінна __ вводиться в базис.

3.2. Розрахунок елементу, що стоїть на місці вирішуємого:

3.3. Розрахунок елементів початкового рядка, що стоїть на місці вирішуємого:

3.4. Розрахунок елементів стовпця, що стоїть на місці вирішує мого:

3.5. Розрахунок решти елементів таблиці:

Аналіз рішення. Значення змінних і цільової функції:

x₁= ; x₂= ; x₃= ;

x₄= ; x₅= ; x₆= ;

Z=

Перевірка виконання обмежень:

1)

2)

3)

4)

Z =