Вопросы для госэкзамена Теория вероятностей

1. Классическое определение вероятности. Основные формулы комбинаторики.

2. Дискретная случайная величина и законы её распределения.

3. Нормальный закон распределения. Правило «трех сигм».

4. Корреляционный момент. Коэффициент корреляции пары случайных величин.

5. Закон больших чисел. Неравенство Чебышева.

Задачи.

1. В лотерее из 50 билетов 5 выигрышных. Какова вероятность того, что среди первых 5 наугад выбранных билетов два будут выигрышными?

Ответ: .

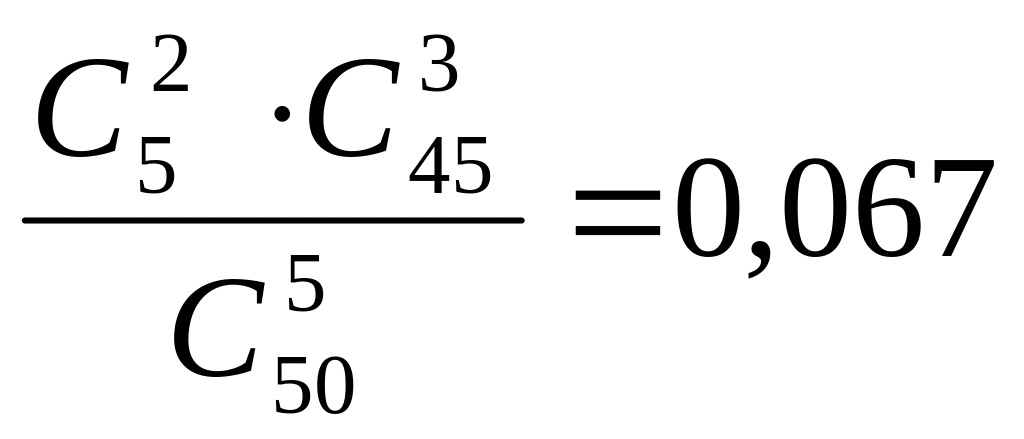2. Изделия имеют скрытые дефекты с вероятностью 0,2. В течение года выходит из строя 75% изделий со скрытыми дефектами и 15% - без дефектов. Найти вероятность того, что изделие имело скрытые дефекты, если оно вышло из строя в течение года.

Ответ: 0,55.

3. Ежедневно новая сделка совершается с вероятностью 0,2 (но не более одной в день). Какова вероятность того, что за 5 дней будет совершено 3 сделки?

Ответ: .

4. Закон распределения непрерывной случайной величины задан функцией Найти М(х), Д(х) и Р(0,5<х<1,5).

Ответ: М(х)= ; Д(х)= ; Р(0,5<х<1,5)=1-1+0,25=0,25.

5. В среднем 10% работоспособного населения некоторого региона – безработные. С помощью неравенства Чебышева оценить вероятность того, что уровень безработицы среди обследованных 10000 работоспособных жителей города будут в пределах от 9 до 10% (включительно).

Ответ: .

Математическая статистика

1. Точечная оценка параметров распределения, предъявляемые к ним требования.

2. Интервальная оценка параметров распределения. Доверительный интервал для неизвестного М_х при неизвестной Д_х.

3. Общая схема проверки статистических гипотез. Ошибки I и II рода.

4. Проверка статистических гипотез. Критерий согласия Пирсона (х²).

5. Проверка гипотезы о равенстве математических ожиданий двух нормально распределенных генеральных совокупностей, дисперсии которых известны.

Задачи

1) Случайная величина Х (число семян сорняков в пробе зерна) распределена по

закону Пуассона . Ниже приведено распределение семян сорняков в n=1000 пробах зерна (х_i – число сорняков в одной пробе, n_i – число проб, содержащих x_i семян сорняков):

хi	0	1	2	3	4	5	6
ni	405	366	175	40	8	4	2

Найти методом моментов точечную оценку параметра . Оценить вероятность того, что в пробе зерна не будет сорняков.

Ответ: .

2) Для отрасли, включающей1200 фирм, составлена случайная выборка из 19 фирм. По

выборке оказалось, что (х – число работающих на фирме человек). Пользуясь 90% доверительным интервалом, оценить среднее квадратическое отклонение для случайной величины Х по всей отрасли, построив доверительный интервал.

Ответ: .

3) По выборке объема n=30 найден средний вес изготовленных на первом станке

изделий, равный 130г; по выборке объема m=40 найден средний вес изготовленных на втором станке изделий, равный 125г. Известны генеральные дисперсии: . Требуется на уровне значимости проверить гипотезу Н₀: а_х=а_у при Н₁: . Предполагается, что случайные величины распределены нормально и выборки независимы.

Ответ: .