
Ітерація 2
f 0 |
180 |
0 |
|
|
0 |
0 |
|
Базові невідомі |
№ рядка |
План (опорний розв'язок) |
x1 |
x2 |
x3 |
x4 |
x5 |
х1 |
1 |
20 |
1 |
|
|
0 |
0 |
x4 |
2 |
66 |
0 |
|
|
1 |
0 |
x5 |
3 |
300 |
0 |
|
|
0 |
1 |
Послідовність заповнення другої та наступних ітерацій така (використовуємо метод Гаусса-Жордана):
Замість базової невідомої х3 (ключовий рядок), вводимо нову базову невідому х1 (невідому ключового стовпчика),
Формально заповнюємо базові стовпчики (пункт 1 ітерації 1).
Ключовий рядок одержуємо від ділення його елементів попередньої ітерації на ключовий елемент.
Усі інші комірки ітерації заповнюємо за правилом прямо кутника:
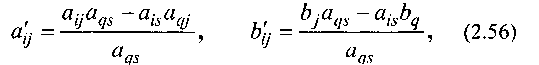
де aij', bi ' відповідно шукані елементи нової ітерації, а аij, bi – попередньої, аqs – ключовий елемент.
![]() ;
; ![]() ;
; ![]()
![]() ;
; ![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
; ![]() ;
;
![]() ;
; ![]() .
.
Після заповнення таблиці -ої ітерації перевіряємо її опорний план на оптимальність. Бачимо, що потрібно перейти до наступного опорного плану, оскільки в нульовому рядку стовпчика "х2" знаходиться від'ємне число ( ).
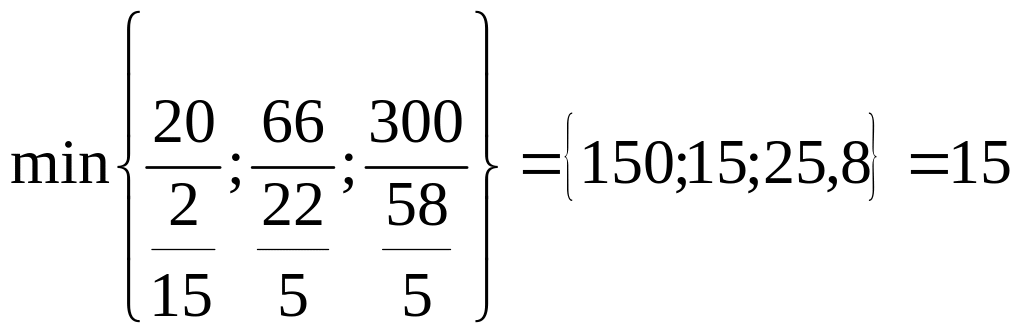 .
.
За ключовий елемент слід взяти число " ".
Ітерація 3
f 0 |
252 |
0 |
0 |
|
|
0 |
|
Базові невідомі |
№ рядка |
План (опорний розв'язок) |
x1 |
x2 |
x3 |
x4 |
x5 |
х1 |
1 |
18 |
1 |
0 |
|
|
0 |
х2 |
2 |
15 |
0 |
1 |
|
|
0 |
x5 |
3 |
126 |
0 |
0 |
|
|
1 |
В ітерації замість базової змінної х4 тепер буде нова базова х2, ключовим буде рядок 2. Над таблицею виконуємо ті ж операції, що й під час другої ітерації.
Після -ої ітерації перевіряємо опорний план на оптимальність. Бачимо, що потрібно перейти до наступного опорного плану, оскільки в нульовому рядку стовпчика "х3" знаходиться від'ємне число ( ).
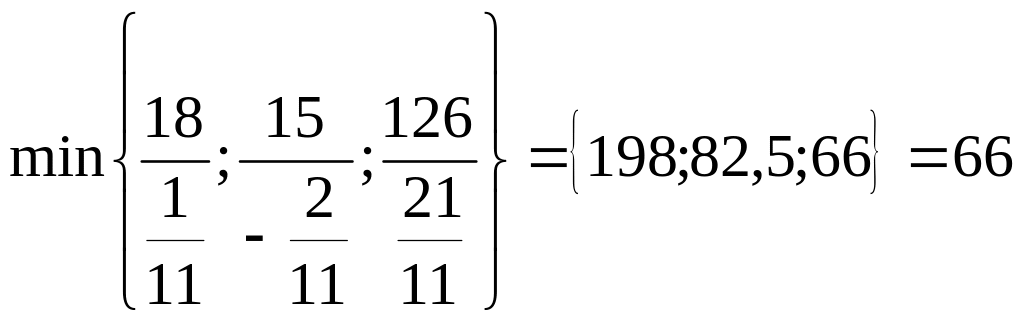 .
.
За ключовий елемент слід взяти число " ".
Ітерація 4
f 0 |
270 |
0 |
0 |
0 |
|
|
|
Базові невідомі |
№ рядка |
План (опорний розв'язок) |
x1 |
x2 |
x3 |
x4 |
x5 |
х1 |
1 |
12 |
1 |
0 |
0 |
|
|
х2 |
2 |
27 |
0 |
1 |
0 |
|
|
х3 |
3 |
66 |
0 |
0 |
1 |
|
|
В рядку 0 вже немає від'ємних чисел, тому опорний план останньої таблиці оптимальний і виписуємо його із стовпчика "опорний розв'язок"
![]()
![]()
![]()
![]()
![]()
![]() .
.
*Зауваження 1. Кожній таблиці відповідає своя канонічна форма стандартного запису. Так, наприклад, за останньою таблицею можна записати таку канонічну форму:
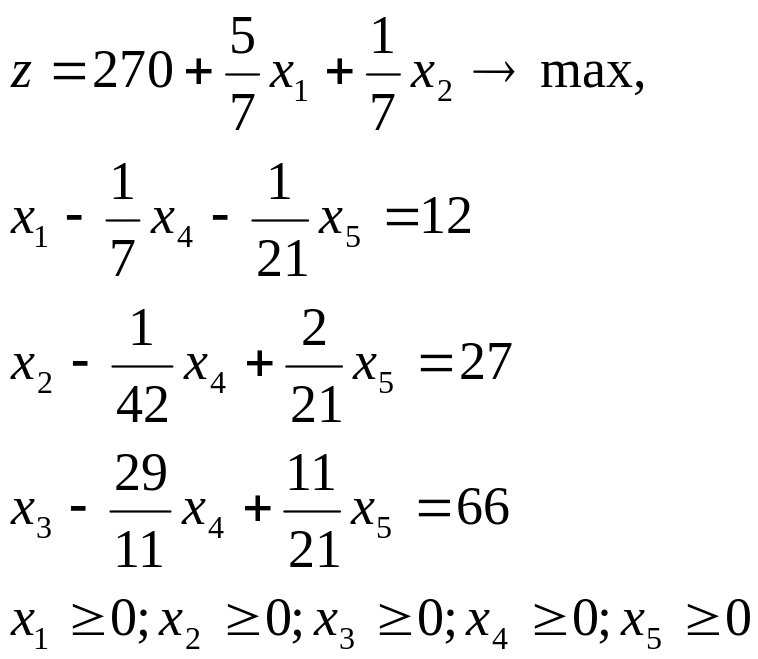
*Зауваження 2. Контролювати правильність обчислення опорних планів і оптимального значення можна за значенням функції мети:
![]()
*Зауваження 3. При розв'язуванні задачі для зручності ітерації послідовно записують одну під одною.
