5.3 Дерева

Теоретичною базою для рекурсивних функцій, що викликають себе більше одного разу, служить розділ дискретної математики, що вивчає дерева.

Основні визначення. Способи зображення дерев

Визначення: Деревом будемо називати кінцеве безліч T, що складається з одного або більше вузлів, таких що:

а) є один спеціальний вузол, званий коренем даного дерева.

б) інші вузли (виключаючи корінь) містяться в попарно підмножинах , що не перетинаються, кожна з яких у свою чергу є деревом. Дерева називаються піддеревами даного дерева.

Це визначення є рекурсивним. Якщо коротко, то дерево це множина, що складається з кореня і приєднаних до нього піддерев, які теж є деревами. Дерево визначається через саме себе.

Але дане визначення осмислено, так як рекурсія скінченна. Кожне піддерево містить менше вузлів, ніж дерево, яке його утримує. Зрештою, ми приходимо до піддерев, що містить всього один вузол, а це вже зрозуміло, що таке.

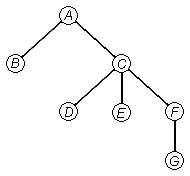
Рис.. Дерево.

Графічно дерево можна зобразити і деякими іншими способами

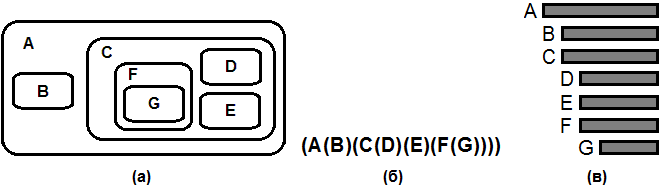
Згідно з визначенням дерево являє собою систему вкладених множин, які або не перетинаються або повністю містяться одна в іншій. Такі множиниі можна зобразити як області на площині (рис. а). На рис. б вкладені множинр розміщені не на площині, а витягнуті в одну лінію. Рис. б також можна розглядати як схему деякої алгебраїчної формули, яка містить вкладені дужки. Рис. в дає ще один популярний спосіб зображення деревовидної структури у вигляді ступінчатого списку.

5.4. Швидкі сортування

Прості методи сортування на зразок методу вибору або методу бульбашки сортують масив з n елементів за O(n2) операцій. Однак за допомогою принципу «розділяй і володарюй» вдається побудувати більш швидкі, що працюють за O (n log2 n) алгоритми. Суть цього принципу в тому, що рішення виходить шляхом рекурсивного поділу завдання на кілька простих підзадач того ж типу до тих пір, поки вони не стануть елементарними.

Алгоритм 1: (quicksort).

1. Вибирається опорний елемент (наприклад, перший або випадковий).

2. Реорганізуємо масив так, щоб спочатку йшли елементи менші опорного, потім рівні йому, потім великі. Для цього достатньо пам'ятати, скільки було знайдено менших (m1) і великих (m2), ніж опорний і ставити черговий елемент на місце з індексом m1, а черговий більший на місце з індексом n-1-m2.

Після виконання такої операції опорний елемент і рівні йому стоять на своєму місці, їх переставляти більше не доведеться. Між «меншою» і «більшою» частинаи масиву перестановок також бути не може. Тобто ці частини можна сортувати незалежно один від одного.

3. Якщо «менша» або «більша» частина складається з одного елемента, то вона вже відсортована і робити нічого не треба. Інакше сортуємо ці частини за допомогою алгоритму швидкого сортування (тобто, виконуємо для неї кроки 1-3).

Як бачите, швидке сортування складається з виконання кроків 1 і 2 та рекурсивного виклику алгоритму для одержані частин масиву.

6.7. Фрактали

Багато об'єктів навколишнього світу мають властивість "самоподібності".

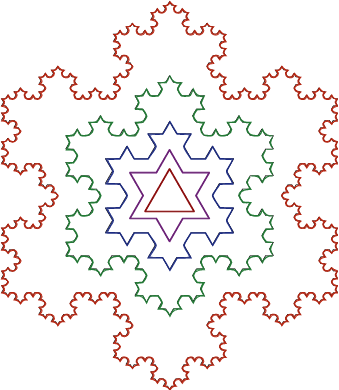
Фракталами називають геометричні фігури, що володіють властивістю самоподібності, тобто складаються з частин, подібних всій фігурі.

Математичний опис нескінченно дробимістю об'єктів рівняннями ліній або поверхонь надзвичайно громіздко через неосяжної кількості найдрібніших об'єктів. Для подолання цієї труднощі математиком Дослідницького центру корпорації IBM Бенуа Мандельброт в 1975 році було введено термін "фрактал" (від латинського fractus - роздроблений, розбитий, що складається з фрагментів), а в 1982 році опублікована основоположна книга "Фрактальна геометрія природи", де описані фрактальні множини, їх властивості, методи одержання та зображення.

Класичним прикладом є крива Коха, побудова якої показано на рис. 12. Спочатку береться відрізок прямої (рис. 12а). Він ділиться на три частини, середня частина вилучається і замість неї будується кут (рис. 12б), сторони якого дорівнюють довжині вилученого відрізка (тобто 1/3 від довжини вихідного відрізка). Така операція повторюється з кожним з вийшов 4-х відрізків (рис. 12в). І так далі (мал. 12г). Крива Коха виходить після нескінченного числа таких ітерацій. На практиці побудова можна припинити, коли розмір деталей виявиться менше дозволу екрану (рис. 12д).

Фрактали, по суті, рекурсивні структури та їх побудову природно проводити за допомогою рекурсивних процедур.

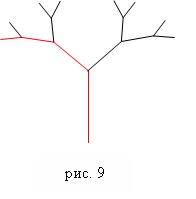
Ще одним прикладом може служити деревце на рис. Воно також містить частини, подібні всьому дереву в цілому, що робить його фракталом.

Розглянемо алгоритм малювання деревця, зображеного на рис.. Якщо кожну лінію вважати вузлом, то дане зображення цілком задовольняє визначенню дерева, даному в попередньому розділі.

Рекурсивна процедура, очевидно повинна малювати одну лінію (стовбур до першого розгалуження), а потім викликати сама себе для малювання двох піддерев. Піддерев відрізняються від базового дерева координатами початкової точки, кутом повороту, довжиною стовбура і кількістю розгалужень (на одне менше). Всі ці відмінності слід зробити параметрами рекурсивної процедури.

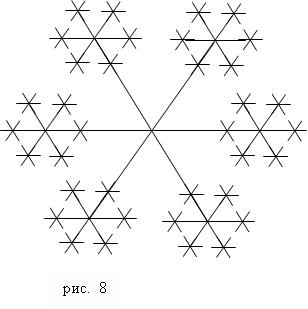
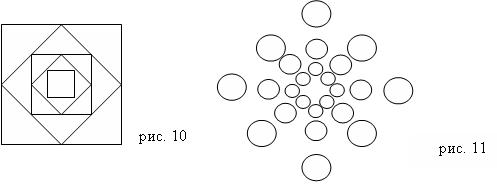
Рекурсивна програма побудови сніжинки

Зображення будується за наступним правилом: будується коло із заданим радіусом r. Потім на діаметрально протилежних точках кола (x-r і x + r) будується знову окружність меншого радіуса (r = 3 r / 5). Для кожної меншою окружності на діаметрально протилежних точках знову будується коло меншого радіусу, і т.д., поки радіус не зменшиться до 10.

Можна також будувати аналогічні сніжинки

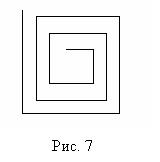
"Множина Кантора".

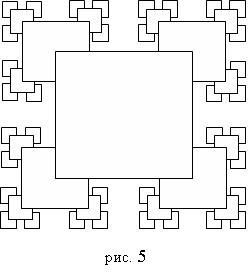
Даний малюнок утворений квадратами. Кожний наступний квадрат в чотири рази менше попереднього. Центр кожного наступного квадрата лежить у вершині попереднього квадрата і т.д. Так як малюнок складається з однотипних елементів, і є явна залежність, як розмірів, так і положення, при створенні даного малюнка можна використовувати рекурсію.

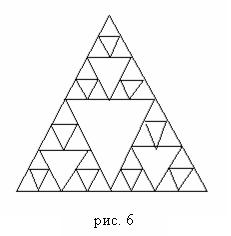
Самим знаменитим прикладом майданного геометричного фрактала є трикутник Серпінського (див. рис.6), що будується шляхом розбиття трикутника, необов'язково рівностороннього - середніми лініями на чотири подібних трикутника,

.