6.3. Математическая модель одноканальной однофазной смо. Показатели ее эффективности

Математическая модель

Состояние однофазной СМО с абсолютно надежными обслужи­вающими приборами в любой момент времени полностью опреде­ляется числом заявок k, находящихся в ней. Действительно, если k  п, то k заявок находятся на обслуживании, очереди нет; k приборов заняты обслуживанием заявок, а n – k приборов свободны. Если k > n, то все приборы заняты (n заявок обслуживается), а k–п заявок находится в очереди.

Величина k может принимать значения k=0, 1, 2, . . ., N, где N = n+m, причем для СМО с отказами m=0, а для систем с неограниченной очередью т и N .

Увеличение числа заявок в системе (переход из состояния S_k в состояние S_k+1) происходит под воздействием потока заявок ин­тенсивности , которая не зависит от k, то есть

_k,k+1 = . (6.1)

Уменьшение числа заявок в системе (переход из состояния S_k в состояние S_k–1) происходит в общем случае под воздействием потока обслуживании интенсивности  и потока уходов заявок из очереди (системы) интенсивности v, причем _k,k+1= f(k, n, , v), а вид этой функции определяется типом СМО.

Из сказанного следует, что однофазной СМО соответствует граф состояний (рис. 6.3), вершины которого (S₀, S₁, S₂, . . .) образуют последовательную цепочку, и любые две соседние вершины соединены двумя встречно-направленными дугами, а процесс ее функционирования представляет собой так называемый процесс «гибели и размножения» (уменьшение и увеличение числа заявок).

Рис. 6.3. Схема однофазной СМО

Определим предельные вероятности состояний Р_k, для СМО с конечным числом состояний. Для СМО P_k, – это вероятность того, что в произвольный момент времени в системе находится ровно k заявок.

В СМО с конечным числом состояний всегда имеет место ста­ционарный режим, так как между любыми двумя вершинами гра­фа существует маршрут.

Уравнения Колмогорова имеют вид:

– состояние S₀

₁₀P₁=₀₁P₀ (6.2)

– состояние S₁

₀₁P₀+₂₁P₂=₁₀P₁+₁₂P₁;

учитывая выражение (6.10), получим

₂₁P₂=₁₂P₁ (6.3)

– состояние S₂

₁₂P₁+₃₂P₃=₂₁P₂+₂₃P₂;

учитывая формулу (6.11), имеем

₃₂P₃=₂₃P₂ (6.4)

— состояние S_k-1 (по аналогии)

_k,k-1P_k=_k-1,kP_k-1 (6.5)

– состояние S_N-1

_N-1,NP_N-1=_N,N-1P_N . (6.6)

Для состояния S_N непосредственно по графу находим уравнение

_N-1,NP_N-1=_N,N-1P_N ,

которое совпадает с уравнением (6.6).

Поэтому последнее уравнение исключаем из рассмотрения, а вместо него используем условие нормировки

. (6.7)

Для решения системы уравнений (6.2) – (6.7) выразим все вероятности через Р₀ и получим

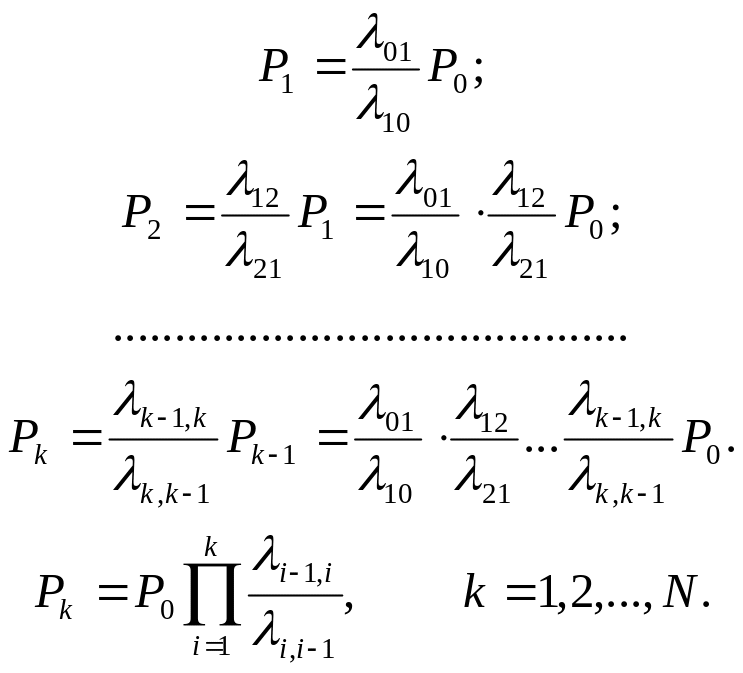. (6.8)

Подставляя значения Р₀ в формулу (6.7), получим

(6.9)

Обратим внимание на структуру формул (6.8) и (6.9). В фор­муле (6.8) имеем произведение отношений интенсивностей пере­хода слева направо к интенсивностям перехода справа налево для всех переходов между начальной и рассматриваемой вершинами графа состояний. В формуле (6.9) имеем сумму этих произведе­ний, вычисленных для всех вершин графа .

Подставляя в формулы (6.8) и (6.9) значения интенсивностей переходов _i,i-1 и _i-1,I, для СМО любого типа можно рассчитать вероятности ее состояний и определить показатели эффективности.

Показатели эффективности

Эффективность СМО характеризует ее приспособленность к выполнению задач по обслуживанию заявок. Показатель эффектив­ности – это количественная мера эффективности, определяющая степень соответствия результатов функционирования СМО целям (задачам), стоящим перед системой.

Рассмотрим наиболее часто используемые показатели эффек­тивности СМО.

1. Вероятность отказа в обслуживании Р_отк – вероятность того, что поступившая в систему заявка не будет обслужена. Это очень важный показатель для СМО.

2. Абсолютная пропускная способность СМО Q – это среднее число заявок, обслуживаемых системой в единицу времени. Для оценки потенциальных возможностей СМО по обслуживанию зая­вок используется номинальная пропускная способность системы:

.

3. Относительная пропускная способность q – это средняя доля заявок, обслуживаемых системой:

. (6.10)

Величину q можно определить и через Р_отк. Действительно, Р_отк – средняя доля времени, в течение которого заявки получают отказ, а следовательно, и средняя доля заявок, не принимаемых системой на обслуживание, то есть

. (6.11)

4. Среднее число занятых приборов

, (6.12)

где – параметр обслуживания (среднее необходимое число обслуживающих приборов).

Производными от данного показателя являются коэффициент занятости (загрузки) приборов K_з и коэффициент их простоя K_п:

, (6.13)

где  – номинальный коэффициент загрузки приборов.

5. Средняя длина очереди L – математическое ожидание числа заявок, ожидающих обслуживания. Производным от показателей N_з и L является среднее число заявок, находящихся в системе,

Y=N_з+L. (6.14)

6. Среднее время ожидания обслуживания – математиче­ское ожидание времени пребывания заявки в очереди.

7. Среднее время пребывания заявки в системе

, (6.15)

где – среднее время от момента начала обслуживания до момента окончания обслуживания ( ).

8. Экономическая эффективность СМО может быть оценена средней прибылью, получаемой в единицу времени при функцио­нировании системы :

, (6.16)

где c₀ – прибыль, получаемая при обслуживании заявки; c – функция стоимости потерь; c_з – стоимость эксплуатации прибора в единицу времени; с_п — стоимость единицы времени простоя при­бора; с_ож – стоимость потерь, связанных с простаиванием заявки в очереди в единицу времени; с_y – стоимость убытков, связанных с уходом заявки из системы.

Выбор показателя для оценки эффективности конкретной СМО определяется как особенностями системы (ее типом) и ее назна­чением, так и задачами проводимого исследования.

Определим показатели эффективности для СМО рассматривае­мых типов, при этом сначала рассмотрим систему с конечной оче­редью, а затем полученные результаты используем при анализе других систем.