4.4. Сетевое моделирование в условиях неопределенности

Теперь обратимся к сетевым моделям, у которых продолжи­тельности работ являются случайными величинами. В этом случае продолжительность критического пути также является случайной величиной; сохраним за ней обозначение Т_кр. Исходная инфор­мация таких моделей содержит сеть, законы распределения веро­ятностей величин t_ij (или вероятностные оценки a_ij, b_ij, m_ij) и (но не обязательно), директивный срок наступления завершающего события Т_дир.

Основными задачами анализа этих моделей являются:

– определение среднего значения и дисперсии критического времени T_кр;

– определение закона распределения величины T_кр;

– определение таких сроков наступления событий, которые с заданной вероятностью не будут превышены;

– определение законов распределения для моментов наступле­ния событий;

– определение вероятности прохождения критического пути через данную работу или совокупность работ.

Существующие аналитические методы решения перечисленных задач весьма громоздки и не нашли практического применения. Более широкое применение получил метод статистических испы­таний.

Далее излагается практически удобный для расчетов метод ве­роятностной оценки наступления завершающего события. Необхо­димо подчеркнуть, что вероятностный анализ для завершающего события особенно важен, поскольку для продолжительности вы­полнения комплекса, как правило, устанавливается директивный срок, и характер распределения случайного реального завершения комплекса работ по отношению к директивному сроку может суще­ственно влиять на принятые решения при управлении выполнением комплекса.

4.5. Анализ соответствия между временем и затратами на выполнение проекта

Рассмотрим следующие задачи вероятностного анализа сверше­ния завершающего события:

– определить вероятность того, что продолжительность крити­ческого пути (выполнения комплекса работ) T_кр лежит в задан­ных пределах

– определить вероятность того, что продолжительность крити­ческого пути не превысит заданный директивный срок;

– определить такой директивный срок, который с заданной ве­роятностью не будет превышен.

В методе приняты некоторые допущения, из которых выделим два основных:

1. Дисперсия D_кр величины критического времени зависит толь­ко от дисперсий работ, лежащих на критическом пути.

2. Величина T_кр распределена по нормальному закону. Это допущение основывается на предположении, что число работ крити­ческого пути достаточно велико и что продолжительности этих работ являются независимыми случайными величинами. Согласно центральной предельной теореме сумма достаточно большого числа независимых случайных величин, сравнимых по дисперсии, при­ближенно распределена по нормальному закону.

Расчет для всех задач начинается с вычисления математических ожиданий продолжительностей t_ij для всех работ комплекса по формуле (4.1) или (4.3). Затем, оперируя величинами как детерминированными:

– вычисляют продолжительность критического пути , представляющую собой математическое ожидание случайной величины T_кр;

– определяют критический путь L_кр;

– вычисляют дисперсии D_ij продолжительностей работ, лежащих на критическом пути, по формулам (4.2) или (4.4);

– на основании известной теоремы, что дисперсия суммы независимых величин равна сумме дисперсий слагаемых, находят дисперсию продолжительности критического пути:

. (4.15)

Теперь при сделанных допущениях можно решить первую из перечисленных выше задач, а именно – определить вероятность того, что продолжительность критического пути лежит в заданных пределах :

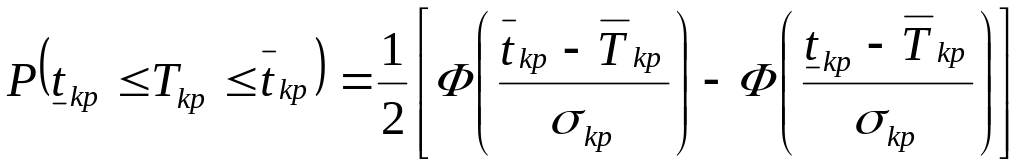, (4.16)

где – функция Лапласа;

t – аргумент функции Лапласа;

– математическое ожидание случайной величины Т_кр;

.

Перейдем ко второй задаче. Согласно принятому допущению случайная величина Т_кр распределена по нормальному закону, по­этому на основании правила трех сигм можно написать:

. (4.17)

Очевидно, что директивный срок должен лежать в тех же пре­делах:

. (4.18)

Действительно, если то вероятность выпол­нения комплекса работ равна нулю; если же взять то без оснований будет растянут срок выполнения комп­лекса.

Кроме того, должно выполняться условие

Т_кр < Т_дир. (4.19)

Из неравенств (4.17), (4.18), (4.19) следует, что

. (4.20)

Теперь можно найти решение второй задачи – определить ве­роятность того, что продолжительность критического пути не пре­высит заданный директивный срок. Искомую вероятность получим из выражения

(4.21)

так как Ф(3) =0,9973.

Третью задачу можно решить следующим образом.

С учетом заданной вероятности Р₃ перепишем выражение (4.21) в виде

. (4.22)

По известным величинам Р₃, и _кр можно определить с помощью таблиц функции Лапласа величину Т_дир, удовлетворяю­щую уравнению (4.22).

Недостаток метода состоит в том, что анализ проводится лишь для одного критического пути. Но при случайных длительностях t_ij совокупность работ, составляющих критический путь, также является случайной и может не совпадать с совокупностью работ анализируемого критического пути. Возможность таких несовпаде­ний возрастает, если имеются полные пути, продолжительность ко­торых незначительно отличается от продолжительности критиче­ского пути. Поэтому для принятия эффективных решений необхо­димо иметь надежные вероятностные оценки длительности работ комплекса.