Нечеткие отношения

Переход от обычного (четкого) отно­шения к нечеткому в принципе тот же, что и переход от обычного множества к нечеткому. В практике чаще используют задание нечетких отношений на обычных множествах.

В этом случае нечетким отношением R на обычном множестве D называется нечеткое подмно­жество прямого декартова произве­дения DXD, характеризующееся функ­цией принадлежности f%: DXD → [0, 1]. Значение µ_R(d,d') этой функции принимается как субъектив­ная мера отношения (d, d') R. Обычное отношение есть частный слу­чай нечеткого отношения с релейной функцией принадлежности:

µ_{R =} ^{1, если (d, d') R}

1, Если (d, d') r. Оценивание предпочтений. Отношения предпочтения и их свойства

Бинарные отношения, являясь уни­версальным способом описания свя­зей между элементами произвольной природы, широко используются в прак­тике принятия решений. С их помощью формально задаются и описываются свойства всех отношений предпочте­ния. Основными отношениями пред­почтения являются следующие:

• отношение строгого предпочтения ;

• отношение безразличия ~.

В этом случае запись d' d" оз­начает, что элемент d' строго предпоч­тительнее элемента d", то есть при предъ­явлении ЛПР только двух указанных элементов оно всегда будет явно пред­почитать элемент d'. Запись d' ~ d" означает, что элементы одинаковы по предпочтительности, и если предъявление ограничить только этими двумя элементами, то ЛПР всегда безраз­лично, какой из них выбрать.

На основе отношений строгого пред­почтения и безразличия вводят до­полнительно: отношения нестрого предпочтения , несравнимости ≥ и неразличимости #, а также различ­ные градации указанных отношений.

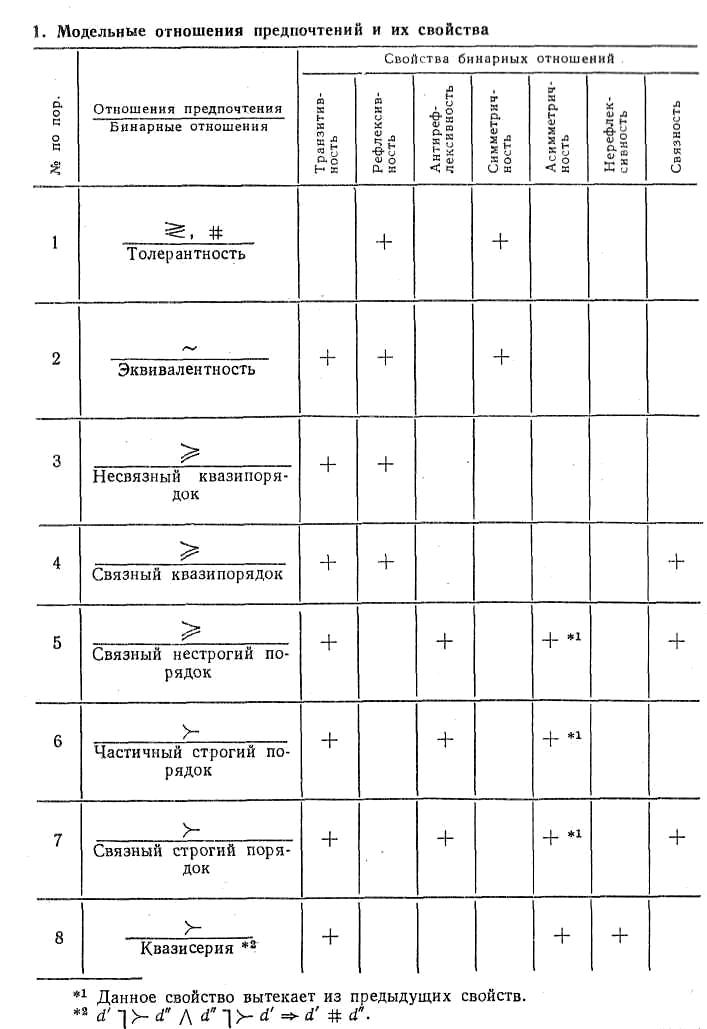
Таблица 1. Модельные отношения предпочтений и их свойства

Отношение нестрогого предпочте­ния d' ≥ d" означает, что элемент d', по мнению ЛПР, не менее предпочти­телен, чем d", то есть при их предъяв­лении ЛПР указывает либо, что d' d"', либо, что d' ~d". Формально отношение ≥ есть объединение U~.

Отношение несравнимости d' # d" означает, что ЛПР не понятно, как выразить отношения между элемен­тами d', d", то есть оно не может одно­значно утверждать, что d' d", или d" d', или d' ~ d".

Отношение неразличимости d' # d" означает, что либо ЛПР не может срав­нить элементы d', d" (d' d"), либо считает их эквивалентными (d' ~ d").

Формально отношения несравнимо­сти и неразличимости можно пред­ставить так:

По смыслу введенные отношения предпочтения обладают следующими свойствами бинарных отношений:

- антирефлексивно и асимме­трично;

~ - рефлексивно и симметрично;

≥ - рефлексивно.

В зависимости от наличия дополни­тельных свойств у указанных отноше­ний вводятся различные их градации, представленные в табл. 1. Отноше­ния 2—8 в табл. 1 охарактеризованы как транзитивные, в общем случае они таковыми могут и не быть (на­пример, если эти отношения выявлены в результате попарного сравнения). Транзитивность теряется в том слу­чае, если ЛПР в процессе контроль­ных предъявлений оценивает объекты по разным целевым признакам. Отно­шение нестрогого предпочтения ^ является следствием нестрогого ран­жирования элементов. В результате этого все множество предъявления элементов разбивается на различаю­щиеся по предпочтительности классы, внутри которых элементы одинаковы по предпочтительности. Если каждый класс содержит только один элемент и проведено нестрогое ранжирование, то такое отношение есть связный не­строгий порядок. Если при этом ран­жирование строгое, — связный стро­гий порядок (серия). Если в каждом классе более одного элемента, прове­дено строгое ранжирование между классами, но внутри класса элементы неразличимы (либо несравнимы, либо эквивалентны), то полученное отно­шение есть квазисерия. Любое частич­ное отношение отличается от связного тем, что классы элементов из множе­ства предъявления нельзя полностью упорядочить по предпочтительности (это можно сделать лишь частично).

В практике выявления и оценива­ния предпочтений обычно стремятся добиться непротиворечивости сужде­ний ЛПР, поэтому везде в дальнейшем всегда будем считать, что отношения строгого предпочтения , безразли­чия ~ и нестрогого предпочтения транзитивны, так что - строгий частич­ный порядок, ~ — эквивалентность, а ≥ — квазипорядок.