Определение коэффициентов относительной важности

Существуют достаточно простые оперативные методы определения коэффициентов относительной важности.

Метод непосредственной численной оценки (М1). Каждому l-му эксперту предлагается непосредственно указать коэффициенты важности αj^(l) элементов d_j, удовлетворяющих условию нормировки:

, .

За групповые оценки α_j в этом случае принимают средние значения:

. (2.45)

Метод балльного оценивания (М2). В заданной балльной шкале каждый эксперт должен оценить элемент d_j Є D. Очень часто выбирают шкалу 0−100; при этом балл 100 соответствует самому предпочтительному элементу.

За групповые оценки принимают числа

, (2.46)

где b_lj – балл, присвоенный j-му элементу l-м экспертом.

Метод относительных частот ран­гов (МЗ). Экспертам предлагается строго упорядочить элементы множества предъявления. Элементам упорядочен­ного множества присваивают числа (обратные ранги), указывающие число элементов, доминируемых данных. Та­ким образом, наилучший элемент будет иметь ранг m − 1 (он лучше всех, кроме самого себя), а наихудший − ранг 0.

Коэффициенты важности

, (2.47)

где r_j^l − ранг, присвоенный j-му элементу l-м экспертом.

Метод попарного сравнения с гра­дациями (М4). Экспертам предлагается произвести попарное сравнение эле­ментов d_i, d_j, руководствуясь задан­ной шкалой выражения предпочтения. Например, можно использовать шкалу со следующими градациями: 1 − эле­менты одинаковы по предпочтитель­ности; 3 − имеются достаточные осно­вания считать один элемент предпочти­тельнее другого; 5 − один элемент, безусловно, предпочтительнее другого. Если эксперт колеблется в оценке предпочтительности между указанными градациями, он ставит промежуточное целое число (2,4). Матрица попарных сравнений в этом случае формируется следующим образом. Последовательно просматривая пары элементов (d_i, d_j), соответствующие строкам i (i = 1, m) матрицы, эксперт выделяет и оцени­вает в заданной шкале только те пары, в которых элемент d_i ≥d_j. Значения остальных элементов a_ji матрицы вы­числяют формально по правилу

,

где a_ji − оценка предпочтительности элемента d_i над элементом d_j по шкале с градациями 1, 2, 3, 4, 5. Это правило соответствует попарному выражению предпочтения как доли относительной интенсивности свойства.

Полученная матрица обрабатывается по алго­ритму 2, в результате чего определяют­ся коэффициенты a_j.

Метод последовательных сравнений(М5) предложен Черчменом и Акофом. Групповые коэффициенты важности определяют осреднением коэффициен­тов важности, получаемых в результате индивидуальной работы каждого экс­перта. Индивидуальная экспертиза в этом случае состоит в следующем.

Алгоритм 3

1. Упорядочить элементы d_j Є D, j = 1, m в соответствии с убыванием их предпочтительности (пусть, например, d₁ > d₂ > d₃ > … > d_m).

2. Каждому элементу d_j приписать вес , причем 0 < < 1, а не обязательно должна быть равна 1. Наиболее важному элементу d₁ соответствует

3. Решить, оказывается ли элемент d₁ предпочтительней всех остальных элементов , вместе взятых²:

а) если d₁ > , то вес корректируется так, чтобы выполнилось неравенство ;

б) если d₁ ~ , то ;

в) если d₁ < , то .

Далее сравнить d₁ с совокупностью и выполнять п. 3 до тех пор, пока не будет справедливо условие а или б для совокупности оставшихся элементов .

4. Сравнить элемент d₂ с совокупностью элементов , 2 по п.3 алгоритма.

5. Для элементов d₃ ,d₄ ,d_m-2 выполнить п. 2-3.

6. Определить коэффициенты важности элементов

.

Если множество предъявлений содер­жит более семи элементов, то непосред­ственное использование описанного ме­тода вызовет серьезные затруднения из-за его громоздкости. Поэтому ис­пользуют следующую модификацию метода.

Алгоритм 4

1. Упорядочить элемен­ты d_j Є D множества предъявлений. Пусть d₁ > d₂ > d₃ > … > d_m.

2. Выбрать элемент d_k, номер которого k определяется с помощью датчика равномерно распределенных чисел^

где r Є (0, 1) − равномерно распре­деленное число, а ]•[ − целая часть числа.

3. Случайным образом разбить оставшееся множество элементов d_j Є D , j ≠ k на непересекающиеся подмножества так, чтобы каждое из них содержало не более шести элементов:

.

4. В каждое из подмножеств D_i, включить элемент d_k, полученный в п. 2:

,

4. Для каждого подмножества D_i, применить алгоритм 3, припи­сав предварительно элементу d_k вес (например, 1,10 или 100). Значения весов α_j остальных элементов подмно­жества корректируют, оставляя вес без изменения.

Сравнить веса , с пред­почтениями, полученными в п. 1. Если получены непротиворечивые резуль­таты, веса нормируют (см. п. 6 алго­ритма 3). В противном случае выявлен­ные противоречия сообщают эксперту и он корректирует значения .

Графоаналитический метод (М6) при­меняют для определения коэффициен­тов относительной важности отдельных характеристик элементов, и в частно­сти показателей эффективности. Коэф­фициенты важности характеристик эле­ментов используют для упорядочения самих элементов по предпочтительно­сти. Например, для упорядочения стра­тегий по предпочтительности с помощью функции эффективности (2.1) по­следнюю часто аппроксимируют линейной сверткой вида

, (2.48)

где α_i − коэффициент важности i-го показателя эффективности W_i, x_i − числовая оценка W_i; n_Q − число част­ных показателей эффективности.

Коэффициенты важности α_i харак­теристик x_i определяют путем под­счета частот предпочтений следующим образом.

В пространстве оценок характери­стик

ограничениями вы­деляется гиперкуб. Рассматривают всевозможные бинарные отношения R_ij на декартовом произведении характеристик :

, (2.49)

где ; ;

− соответствующая наихудшая, средняя и наилучшая оценки X_i характеристики X_i.

Таким образом, бинарное отношение R_ij включает упорядоченные пары оценок характеристик (X_i, X_j), имею­щих по три градации без наилучшей и наихудшей пар. Бинарные отношения представляют графически в декартовой системе ко­ординат (рис. 2.5, а).

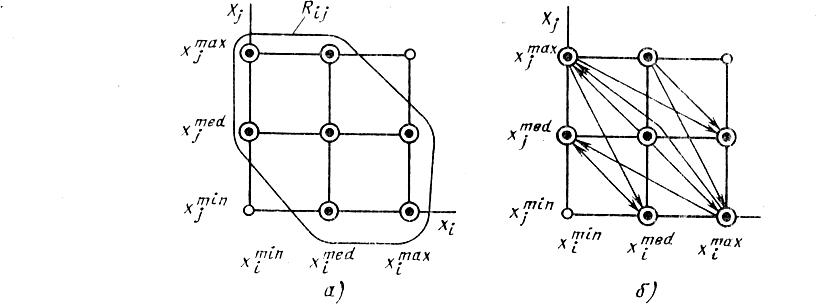
Рис. 2.5. Бинарные отношения R_ij (a) и граф предпочтений (б)

Коэффициенты важности вычисляют по следующему алгоритму.

Алгоритм 5

Сравнить гипотетиче­ские элементы с характеристиками, принадлежащими R_ij, по предпочти­тельности и отразить суждение в виде стрелки, направленной от более пред­почтительного элемента к менее предпочтительному³ (см. рис. 2.5,б).

2. Подсчитать число а_ij^{( l )} стрелок, направленных от характеристики X_i к характеристике X_j.

3.Определить частоту P_ij предпочтения характеристики X_i над характеристикой X_j:

i < j; . (2.50)

4.Рассчитать коэффициенты относительной важности характеристик X_i:

. (2.51)

5. Вычислить групповые коэффи­циенты важности (если число п экспер­тов больше 1):

. (2.52)

Для примера, представленного на рис. 2.5, число a_ij стрелок, направлен­ных от характеристики Х_i к характе­ристике X_j, равно 3.

Следовательно,

.

Если используются шкалы оценок X_j с числом градаций k, большим трех, то вместо цифры в знамена­теле следует поставить величину

.

Метод свертки (М7). Функция эффективности может быть задана в виде некоторой свертки частных характе­ристик X_i (например, частных пока­зателей эффективности Wi), взвешен­ных коэффициентами их важности. Если вид функции эффективности W_e (X) определен (в простейшем слу­чае в виде линейной свертки (2.48)), то, используя элементарные суждения относительно контрольных предъяв­лений, составляют соответствующие соотношения по правилу (2.5). В ре­зультате получают систему равенств и неравенств, решая которую опре­деляют коэффициенты важности. По­скольку эта система соотношений мо­жет оказаться несовместной, то ее регуляризуют, подбирая такие коэф­фициенты a_i, чтобы обеспечить наи­меньшую степень ее несовместности.

Алгоритм 6

1. В пространстве ха­рактеристик выделить гиперкуб, задаваемый систе­мой неравенств .

2. Любым способом¹ отобрать из гиперкуба m₀ пар оценок a, b Є X, c, d Є X; …; q, h Є X, причем m₀ ≥ n₀.

3. Сравнить полученные пары оценок по предпочтительности и составить систему соотношений по правилу:

(2.53)

где − функция свертки.

4. Составить функцию невязки

, (2.54)

где R₁ − множество пар, у которых X > Y R₂ − Z ~ U .

Примечание. Обычно строят равномерную решетку либо с помощью датчика случайных чисел или ЛП_τ – последовательностей генерируют необходимое число точек.

5. Решить задачу нелинейного программирования:

(2.5.15)

при ограничениях α ≥ 0,

Если в экспертизе участвуют не­сколько экспертов, то коэффициенты важности, полученные для каждого из п экспертов по алгоритму 6, осредняют по (2.52).

При выборе конкретного метода оп­ределения коэффициентов относитель­ной важности следует учитывать сле­дующие обстоятельства: во-первых, ог­раничения по допустимому времени общения с экспертами, во-вторых, тре­буемую надежность получаемых оце­нок, в-третьих, наличие ЭВМ и мате­матического обеспечения, позволяю­щих провести обработку результатов (сложность обработки).

По первому показателю эти методы можно упорядочить следующим обра­зом:

,

где М8 — метод Терстоуна; М9 — метод попарного сравнения.

По второму показателю ряд пред­почтений выглядит следующим обра­зом:

.

По третьему показателю методы упо­рядочиваются так:

.

Методы МЗ, М8 используют только при групповой экспертизе, в то время как остальные можно применять и при индивидуальном экспертном оп­росе.

Вопросы для самопроверки по разделу 2

1. Что понимается под предпочтением?

2. Какая система обладает свойством полноты?

3. Что необходимо уметь ЛПР при исследовании возможных способов выявления системы предпочтений?

4. Какие способы выражения предпочтений вы знаете?

5. Что такое матрицы попарных сравнений?

6. Что понимается под сортировкой?

7. Для чего применяется ранжирование?

8. В чем отличие способа попарного сравнения от способа попарного выражения предпочтения как доли суммарной эффективности?

9. На чем основан способ выражения предпочтений лингвистическими переменными

10. Что такое отношение?

11. Какие свойства бинарных отношений вы знаете?

12. Какое отношение называется толерантностью?

13. Какая операция называется транзитивным замыканием отношения?

14. Какое соответствие называется функцией выбора?

15. Какую функцию называют функцией эффективности?

16. Что понимают под методом экспертного оценивания?

17. Какие методы индивидуального экспертного оценивания вы знаете?

18. Какие методы группового экспертного оценивания вы знаете?

19. Что понимается под организацией экспертного оценивания?

20. Какие этапы экспертного оценивания вы знаете?

21. Как вычисляется коэффициент компетентности эксперта?

22. Как вычисляется коэффициент информативности эксперта?

23. Что позволяет оценить статистическая оценка полученных результатов?

24. Какие формы выражения суждений экспертов вы знаете?

25. Какие методы определения коэффициентов относительной важности вы знаете?

1 Часто эту функцию называют функ­цией ценности или функцией полезности. Эти названия укоренились с тех пор, когда ошибочно считали, что каждому элементу из предъявленной совокупности присуща некоторая объективная полезность (цен­ность), которую и отражают субъективные предпочтения ЛПР. Авторы считают тер­мин «функция эффективности» более со­ответствующим смыслу задач принятия решений на основе анализа результатов оценивания эффективности операции.

2 Суждение о предпочтительности над совокупностью остальных элементов де­лается с учетом диапазона ожидаемых значений характеристик рассматриваемых элементов.

3Стрелки связывают только пары эле­ментов, лежащих в направлении «северо-запад» − «юго-восток» рассматриваемой декартовой системы. Это обусловлено тем, что предпочтение между парами элементов в направлении «северо-восток» − «юго-запад» очевидно.

119