2.6. Оценка согласованности мнений экспертов

Приведенные в примере 2.8 нестрогие ранжировки мероприятий получены в результате формирования группового мнения экспертов. Групповое мнение можно формировать только тогда, ког­да индивидуальные предпочтения эк­спертов хорошо согласуются. Для оценки согласованности мнений в груп­пе применяют два способа. Первый способ основан на вычислении сред­них значений коэффициентов парной корреляции:

; (2.12)

; (2.13)

где l, i – номера экспертов (l, i = 1, n ); τ_li и ρ_li – парные коэффициенты корреляции по Кендаллу и Спирмену соответственно.

Этот способ удобно применять при малом числе п экспертов. В случае полной согласованности мнений эк­спертов средние значения коэффици­ентов τ иρ принимают значения, рав­ные 1.

Второй способ основан на вычисле­нии специальных коэффициентов со­гласованности коэффициента конкордации С_К Кендалла и энтропийного коэффициента согласия С_Е.

Коэффициент конкордации Кендалла имеет различный вид в зависимости от типа ранжирования. При строгом ранжировании

, (2.14)

где

; (2.15)

где r_li – ранг i-го элемента, присвоенный l-м экспертом; m – число оцениваемых элементов; n – число экспертов.

Для нестрогих ранжировок коэффициент конкордации Кендалла

, (2.16)

где

; (2.17)

где t_k − число одинаковых рангов в k-й группе нестрогих рангов в ранжировке l-го эксперта; T_l — число групп оди­наковых рангов в ранжировке l-го эксперта.

Коэффициенты (2.14) и (2.16) рав­ны 1 в случае полного совпадения мнений экспертов и равны 0 в случае их полной несогласованности (0 ≤ C_K, C_K ≤ 1). Статистическая про­верка значимости полученных коэф­фициентов конкордации осуществля­ется обычным порядком при исполь­зовании правосторонней критической области C_K≥C_α. Ранее были приведены значения вероятностей:

для m = 3÷10 и n=3÷5. Для m > 7 используют таблицы распределе­ния χ² для величины п (т−1)С_К cm−1 степенями свободы, которая линейно связана с коэффициентом кон­кордации.

Согласованность экспертов удовлетворительная, если и α ≤ 0,01, и хорошая, если и α < 0,001.

Энтропийный коэффициент согласия

, (2.18)

где энтропия

; (2.19)

где P_lj – оценка вероятности l-го ранга, присваиваемого j-му элементу. Эти оценки вероятностей вычисляют как отношение числа экспертов n_lj, присвоивших элементу j ранг l, к общему числу экспертов n:

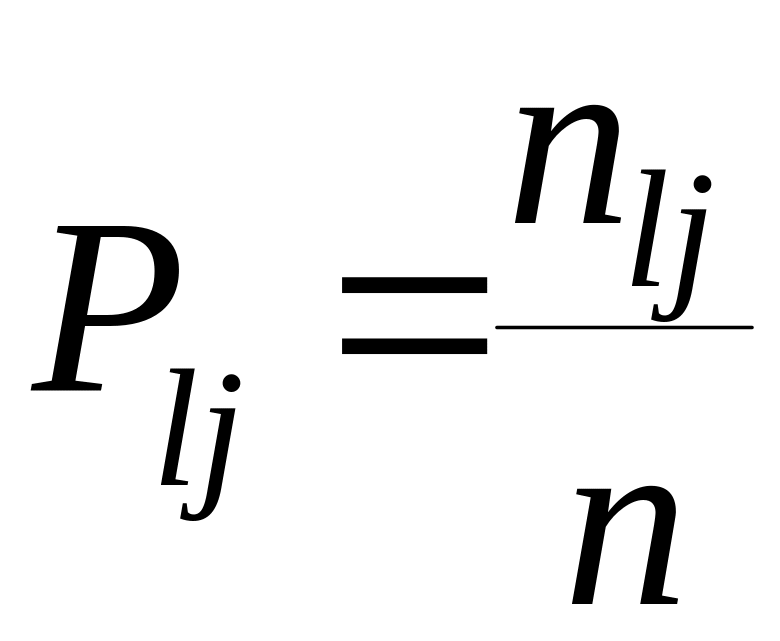; (2.5.16)

Энтропийный коэффициент согласия изменяется от 0 до 1.

Использование коэффициентов сог­ласия С_K и С_E обеспечивает примерно одинаковые результаты при близких мнениях экспертов. Для вычислений проще использовать коэффициент С_K. Однако если эксперты в своих мнениях разделились на две подгруппы, даю­щие противоположные ранжировки, то коэффициент С_K обратится в нуль, а С_E будет больше 0,5. Таким образом, использование энтропийного коэффи­циента согласия позволяет достаточно легко установить наличие двух про­тивоположных в своих суждениях подгрупп.

Если в результате анализа выявлено, что согласованность экспертов неудов­летворительна (либо малы значения коэффициентов , либо они незначимо отличны от нуля), необходимо произвести содержатель­ный анализ причин расхождения мне­ний. Ими могут быть: наличие в группе экспертов с оригинальными мнениями (резко отличающимися от мнений ос­тальных); разделение экспертов на несколько групп, придерживающихся своей точки зрения, и др. Одним из методов, позволяющих согласовать мне­ния или окончательно разделить экспертов на подгруппы, является метод Дельфи.

Проверив согласованность мнений экспертов (в том числе в выделенных подгруппах) и убедившись, что она достаточно высока, формируют груп­повое мнение. Его осуществляют либо с помощью средних рангов, набранных каждым элементом:

, (2.21)

либо отысканием некоторой ранжировки, которая наиболее тесно коррелирована с остальными:

,

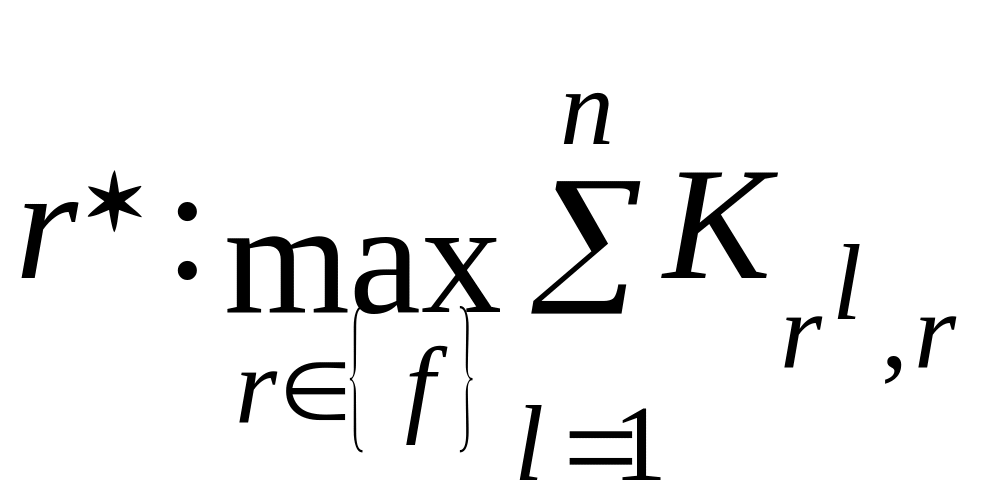где r^* − искомая групповая ранжировка r^*=(r₁,r₂,….,r_m)^T; {f} – множество всевозможных ранжировок (в том числе и нестрогих), построенных на m элементах множества предъявления; − коэффициент корреляции Кендалла или Спирмена между ранжировкой r^l l-го эксперта и ранжировкой r{f} либо минимизацией специально выбранной метрики χ на множестве квазипорядков.

В последнем случае каждая ранжировка r^l l-го эксперта рассматривается как точка в m-мерном пространстве квазипорядков. Обычно используют метрику Хемминга:

, (2.22)

где − элементы матрицы попарных сравнений элементов d_i, d_j, i, j = 1, m, построенные по ранжировке l-го эксперта:

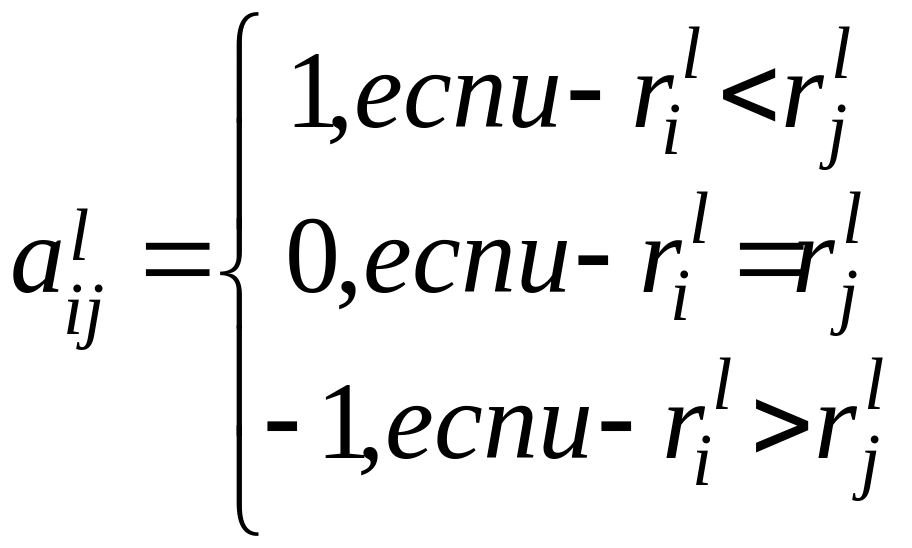; (2.23)

где − ранг i-го элемента в ранжировке l-го эксперта в прямой нумерации рангов.

С использованием введенной метрики χ групповая ранжировка определяется либо как медиана:

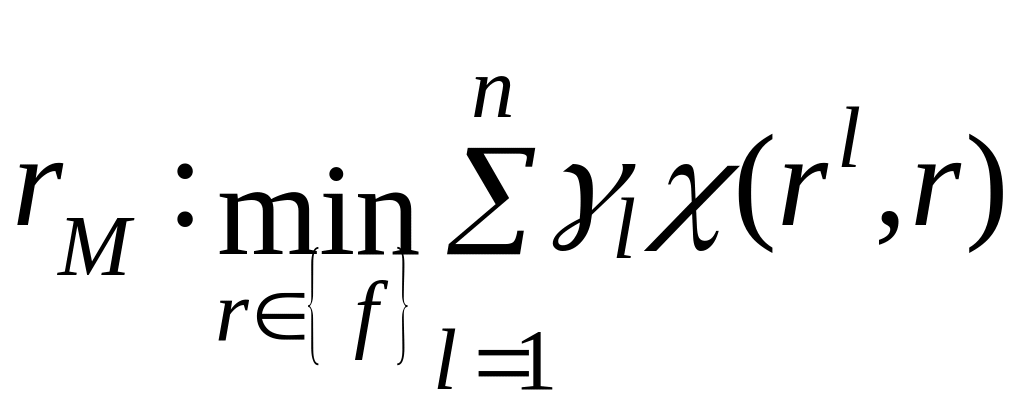, (2.24)

либо как средняя ранжировка:

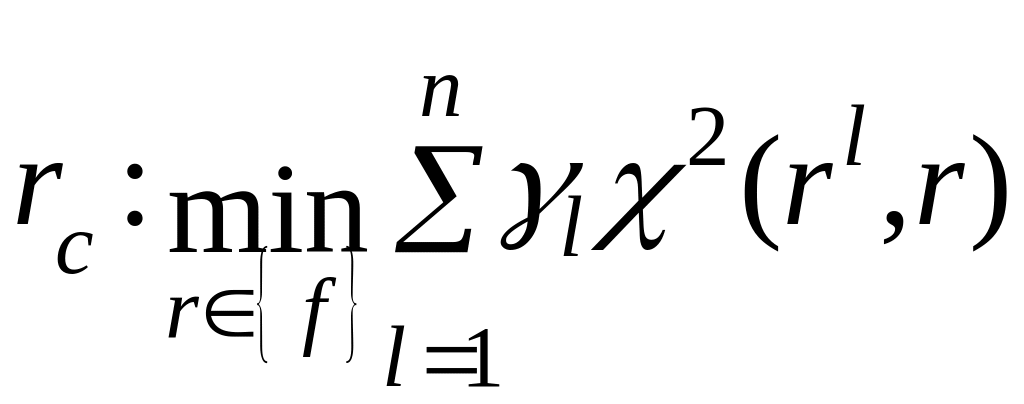, (2.25)

где γ_i − коэффициент компетентности l-го эксперта .

При ранжировании элементов по нескольким характеристикам вначале отыскивается «медианное мнение» l-го эксперта по всем характеристикам (с учетом их весов):

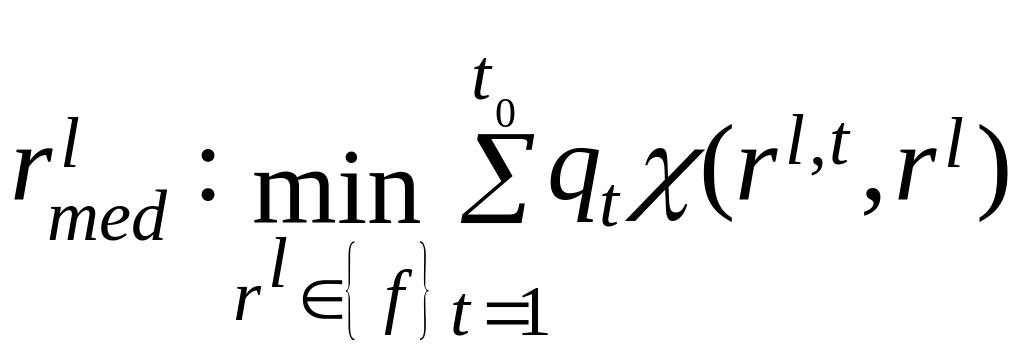, l=1,n, (2.26)

где q_t − коэффициент важности t-й характеристики (t=1, t₀): r^{l, t} − ранжировка элементов по t-му признаку l-м экспертом, а затем по (2.5.20) с подстановкой вместо r^l ранжировки r^l_med определяется групповая ранжировка r_M.

Задачи (2.22), (2.24)—(2.26) яв­ляются сложными для вычисления, поэтому групповую ранжировку опре­деляют упорядочением по суммарным рангам (2.21). Для учета компетен­тности экспертов (2.21) трансформи­руют следующим образом:

. (2.27)

Построение групповой ранжировки по суммарным взвешенным рангам (2.27) при хорошей согласованности экспертов обеспечивает практически одинаковые результаты с решениями задач (2.24) и (2.25).

Построить групповую ранжировку можно с помощью перехода от инди­видуальных ранжировок к матрицам попарных сравнений и вычислений собственного вектора. Этот подход более обоснован в теоретическом от­ношении.

Таблица 2.3. Распределение коэффициента конкордации

m=3
n = 3		n = 4		n = 5		n = 6		n = 7		n = 8		n = 9
Sα	α	Sα	α	Sα	α	Sα	α	Sα	α	Sα	α	Sα	α
6	0.528	8	0.431	14	0.367	18	0.252	24	0.237	26	0.236	32	0.187
8	0.361	14	0.273	18	0.182	24	0.184	26	0.192	32	0.149	38	0.154
14	0.194	18	0.125	24	0.124	26	0.142	32	0.112	38	0.120	42	0.107
18	0.028	24	0.069	26	0.093	32	0.072	38	0.085	42	0.079	50	0.069
		26	0.042	32	0.039	38	0.052	42	0.051	50	0.047	56	0.048
		32	0.0046	38	0.006	42	0.029	50	0.027	56	0.030	62	0.031
				42	0.0009	50	0.012	56	0.016	72	0.0099	78	0.010
				50	0.0008	54	0.0081	62	0.0084	78	0.0048	86	0.0006
						56	0.0055	72	0.0036	86	0.0024	98	0.0029
						62	0.0017	78	0.0012	98	0.0009	104	0.0013
						72	0.0001	96	0.0003			114	0.0007

m = 3		m = 4								m = 5
n = 10		n = 3		n = 4		n = 5		n = 6		n = 3
Sα	α	Sα	α	Sα	α	Sα	α	Sα	α	Sα	α
32	0.222	19	0.342	32	0.200	41	0.210	46	0.218	46	0.213
42	0.135	21	0.300	36	0.158	43	0.162	52	0.163	50	0.163
50	0.092	25	0.207	40	0.105	51	0.107	62	0.108	56	0.096
56	0.066	27	0.175	46	0.068	57	0.075	68	0.073	60	0.063
62	0.046	29	0.148	50	0.052	61	0.055	74	0.056	62	0.056
74	0.026	33	0.075	54	0.033	67	0.034	80	0.037	66	0.038
86	0.012	35	0.054	62	0.012	81	0.012	100	0.010	74	0.015
96	0.0075	37	0.033	66	0.0062	85	0.0067	108	0.0061	78	0.0053
104	0.0034	41	0.017	70	0.0027	93	0.0023	118	0.0028	82	0.0028
122	0.0013	45	0.0017	74	0.0009	101	0.0014	128	0.0009	86	0.0009
126	0.0008					105	0.0006