2. Поставлена задача

У цій роботі вирішується наступна задача. Нехай є сферичне тверде тіло радіуса R і щільності ρ_т. Необхідно розглянути рух цього тіла у в'язкій рідині щільності ρ _рід. з коефіцієнтом в'язкості η, вважаючи, що в початковий момент тіло знаходиться на початку координат і має нульову швидкість. При цьому враховується дія на тіло наступних сил: сила тяжіння, сила Архімеда і сила внутрішнього тертя рідини.

Необхідно скласти рівняння руху тіла в цій системі, написати на мові програмування Сі програму для вирішення цього диференціального рівняння методом Рунге-Кутти. Також необхідно знайти точне рішення рівняння і порівняти обидва рішення.

Програма повинна приймати наступні вхідні параметри: параметри фізичної моделі - радіус тіла, густина тіла, щільність рідини, коефіцієнт в'язкості рідини; параметри методу Рунге-Кутти - кінцевої точки, в якій і обчислюється значення, і величина кроку h.

Розділ 2. Методика

1. Метод Рунге-Кутти

У загальному вигляді сімейство методів Рунге-Кутти для одного диференціального рівняння першого порядку полягає в наступному. Нехай є задача Коші:

 для х > x_0, u (x₀ )= u₀

і нехай чисельне рішення задачі Коші відомо в точці x_n, а саме 

y (x _n )= y _n. Тоді m-етапний метод Рунге-Кутти (метод Рунге-Кутти m-го порядку) буде полягати в наступному. Задаються деякі числові коефіцієнти a _i, b _ij, i = 2, 3, ... m; j = 1, 2, ... (m-1), σ _l, l = 1, 2, ... m і послідовно обчислюються наступні функції:

k ₁ = f (x _n, y _n )

k ₂ = f (x _n + a ₂ h, y _n + b ₂₁ hk ₁)

k ₃ = f (x _n + a ₃ h, y _n + b ₃₁ hk ₁ + b ₃₂ hk ₁)

...

k _m = f (x _n + a _m h, y _n + b _m1 hk ₁ + ... + b _{m, m-1} hk _m-1)

Потім з формули

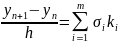
знаходиться рішення задачі в наступній точці (x _n+1): y (x _n+1) = y _n+1. 

При цьому потрібно, щоб виконувалась умова:

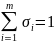
Методи порядку 5-го і вище використовуються рідко, найчастіше застосовуються методи четвертого порядку. При цьому найбільш популярним з них, є так званий метод Рунге-Кутти:

k 1 = f (x n, y n );

k 2 = f (x n + h / 2, y n + k 1 h / 2);

k 3 = f (x n + h / 2, y n + k 2 h / 2);

k 4 = f (x n + h, y n + k 13 h);

2. Інструмент. Мова програмування Сі

Мова програмування Сі є одним з найпопулярніших мов високого рівня. Її особливостями є висока ефективність, універсальність, відносна простота, а також широка підтримка з боку розробників програмного забезпечення. Існує величезна кількість компіляторів мови для більшості платформ, а також безліч бібліотек, що розширюють функціональність програм, написаних на ньому.

Завдяки цим особливостям Сі є найпопулярнішою мовою системного програмування, а також широко використовується при створенні прикладного програмного забезпечення.

Мова Сі справила великий вплив на розвиток мов програмування. Так, вона послужила основою для багатьох мов, у тому числі для популярних мов C + + і нащадків останньої мови (наприклад, C #); також багато відомих мови запозичили синтаксис мови Сі.

На даний момент Сі є стандартом де-факто швидкодії та ефективності серед мов програмування високого рівня.