Статистичні методи встановлення емпіричних залежностей

При емпіричному (експериментальному) вивченні функціональної залежності величини у від величини х замірюють величину при різних значеннях х. Результати можуть бути представлені у вигляді таблиці 12.3. або графічно.

Задача зводиться до аналітичного представлення шуканої функціональної залежності, тобто до підбору формули, яка описує результати експерименту. Особливість задачі полягає в тому, що наявність випадкових похибок зміни ("шуму" в експерименті) робить нерозумним добір такої формули, яка точно відповідала б усім дослідним значенням. Отже, графік шуканої величини не повинен проходити через усі точки, а повинен по можливості згладжувати "шум". Однак, згладжування "шуму" буде більш точним і надійним, чим більше проведено експериментів (тобто чим більше надмірної інформації). Наприклад, для проведення прямої у = ах + b цілком достатньо двох точок (х₁,у₁) та (х₂;у₂). Але при наявності більш значного "шуму" для тієї ж мети може знадобитися декілька десятків точок.

Таблиця 12.3

Результати експериментів

x	x1	x2	x3	…	xk;…	xn
y	y1	y2	33		yk;…	yn

Емпіричну формулу зазвичай вибирають з формул певного типу (наприклад, у = ах + b,у = ае^bх +c).

Іншими словами, задача зводиться до визначення параметрів а,b,с,... формули, в той час, як вид формули визначається, виходячи з теоретичних припущень або з міркувань простоти аналітичного уявлення матеріалу.

Найбільш простий спосіб переконатися в необхідності підбора для отриманих даних лінійної функції – графічний. Нанесемо дані досвідів на графік, що зручніше за все будувати на міліметровому папері. Дослідні дані, розташовані у виді точок поблизу прямої, будуть свідчити про лінійну функцію. Якщо це так, то лишається лише визначити коефіцієнти а та b.

Розглянемо три основних способи визначення коефіцієнтів: натягнутої нитки, середньої і найменших квадратів. Перші два способи дають менш точні результати, однак є більш простими, ніж спосіб найменших квадратів.

Спосіб натягнутої нитки полягає у тому, що експериментальні значення наносять на міліметровий папір та проводять пряму, яка найближче всього проходить до цих точок. Вибирають дві довільні точки на прямій (тому спосіб часто називають також способом обраних точок) та визначають їх координати (х₁,у₁) та (х₂;у₂). Тоді для визначення коефіцієнтів а та Ь отримають два простих рівняння:

y₁ = а₁х + b₁; y₂ = а₂х + b₂ (12.34)

Спосіб середньої не потребує графічного зображення експериментальних даних і полягає у наступному. Нехай значення, що спостерігалися, наведені у таблиці 12.3.

Навіть якщо між x та у теоретично встановлено лінійну залежність y=ах+b. значення у;, які спостерігаються, будуть відрізнятися від ах_i+b внаслідок наявності експериментальних похибок. Експериментальна похибка

Δ_i = y₁ – ax_i – b, i = 1,2,…,n.

Якщо обирати параметри а та b, так щоб для всіх n спостережень похибки врівноважувалися, тобто то це привело б до отримання одного рівняння, тоді як для находження коефіцієнтів а та b їх необхідно два. Тому припустимо, що врівноваження відбувається не тільки для всіх здійсненних спостережень в цілому, але й для кожної групи, яка містить половину (або майже половину) всіх спостережень окремо. У такому випадку прийдемо до системи рівнянь, яка може бути записана наступним чином:

(12.35)

де т – число спостережень у першій групі, яке може бути обрано довільно.

Звичайно, т обирають таким чином, щоб число спостережень у другій групі дорівнювало також т, якщо п парне, та т±1, якщо и непарне. Отриману систему для визначення коефіцієнтів а та b записують у наступному вигляді:

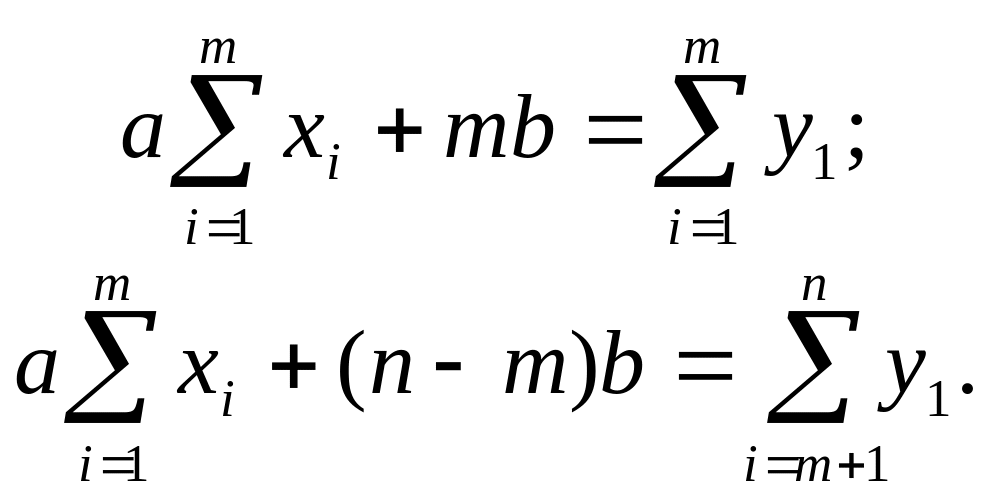
(12.36)

Спосіб найменших квадратів полягає у тому, що якщо всі значення функції у₁,у₂,…,y_n виміряні з однаковою точністю, то оцінки параметрів а_о,а₁,....а_п проводять за умови: сума квадратів відхилень значень у_к, що заміряні, від розрахункових f_N(х_к;а_о,а₁,...а_n), тобто:

(12.37)

приймає найменше значення.

Вишукування тих значень параметрів а_о,а₁,...а_n, що призводять до найменшого значення функції S = S(а_о,а₁,...а_n), зводиться до рішення системи рівнянь

(12.38)

Аналогічно визначається коефіцієнти для ступеневих функцій виду у = ах^b. Такий вид функції зазвичай спостерігається в залежності подовження тканини від прикладеного навантаження. Легко помітити, що функція даного виду зображується у вигляді прямої лінії у логарифмічних осях. Дійсно, після того як проведено логарифмування вказаного рівняння з припущенням, що lgх = Х; lgу= У; lgа = A, можна отримати рівняння

Y = A + bX. (12.39)

Для оцінки точності цієї формули необхідно, щоб результати спостережень розміщалися на логарифмічній сітці поблизу прямої лінії.

Приклад 7

Необхідно визначити залежність вологості у, % шкіри від часу сушіння х, хв., при температурі 60°С. Об'єм вибірки - шість дослідів. Експериментальні дані представлені нижче.

x	y	x	y
0	32	10	17
5	25	15	11
8	20	20	5

Визначимо коефіцієнти рівняння у = ах + b. Для цього представимо експериментальні лані у вигляді таблиці 7.2.

Таблиця 12.4

x	y	x2	xy	y2	x+y	(x+y)2
0	32	0	0	1024	32	1024
5	25	25	125	625	30	900
8	20	64	160	400	28	784
10	17	100	170	289	27	729
15	11	225	165	121	26	676
20	5	400	100	25	25	625
58	110	814	720	2484	168	4738

Наведемо основні формули для розрахунку коефіцієнтів:

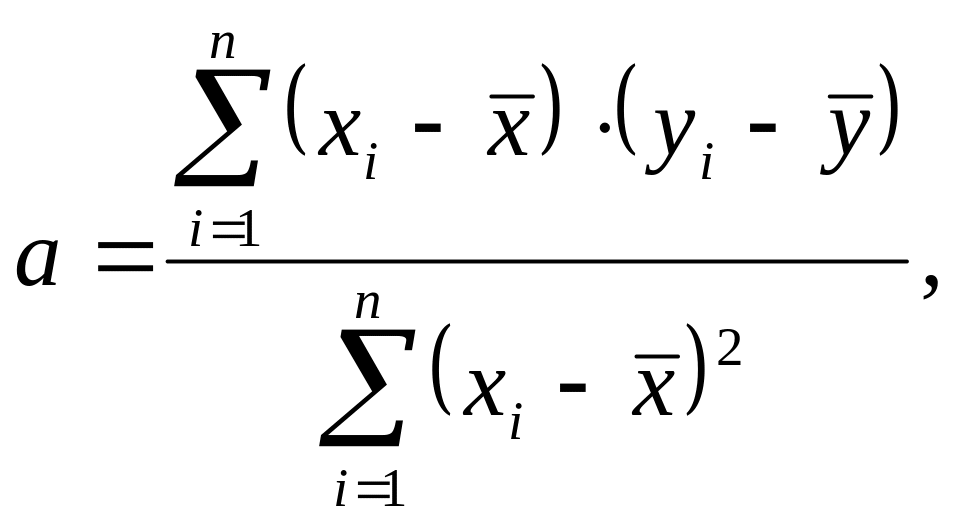(12.40)

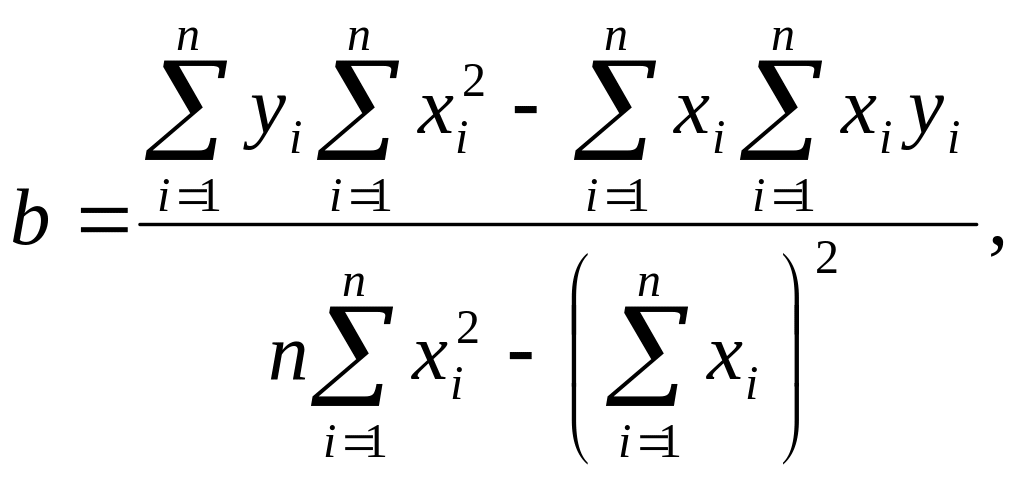(12.41)

Використовуючи отримані у табл. 12.4 суми для визначення коефіцієнтів а та b. отримаємо:

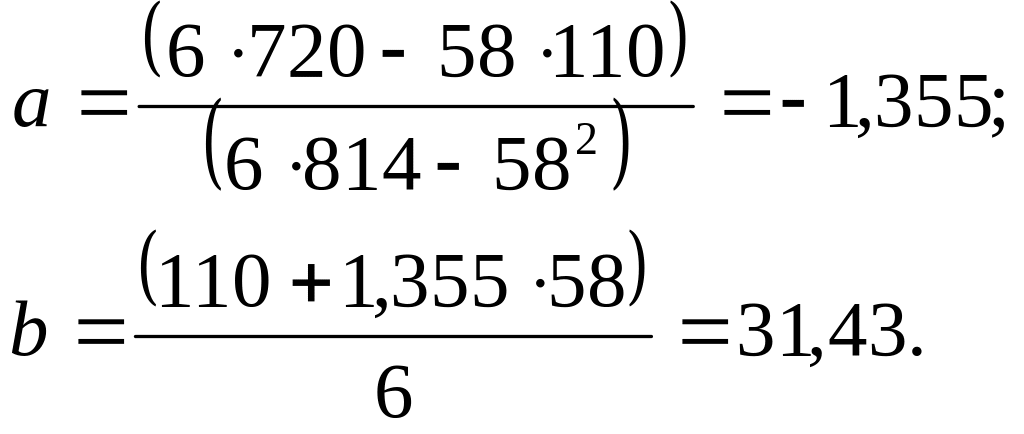
Розрахунки можна перевірити за формулою:

(12.42)

У даному випадку маємо 4738 = 814 + 2-720 + 2484, тобто розрахунки виконано вірно. Отримано рівняння: y = 31,43-1,355x.