Основні тригонометричні співвідношення.

1. Співвідношення між тригонометричними функціями одного й того самого аргументу.

1) sin²α +cos²α=1; 2) tgα∙ctgα=1;

3) tgα= ; 4) ctgα= ;

5) 1+tg²α= ; 6) 1+ctg²α= ;

7) sin²α =1 - cos²α= ;

8) cos²α=1 - sin²α = ;

9) tgα= , 10) ctgα= ,

11) tg²α= ,

12) ctg²α= .

2. Формули додавання (віднімання) аргументів.

13) sin(α+β)=sinα∙cosβ+cosα∙sinβ,

14) sin(α-β)=sinα∙cosβ-cosα∙sinβ,

15) cos(α+β)=cosα∙cosβ-sinα∙sinβ,

16) cos(α-β)=cosα∙cosβ+sinα∙sinβ,

17) tg(α+β)= ,

18) tg(α-β)= ,

19) ctg(α+β)= ,

20) ctg(α-β)= ,

3.Формули подвійного і потрійного аргументу.

21) sin2α=2sinα∙cosα,

22) cos2α=cos²α-sin²α=2cos²α-1=1-2sin²α,

23) tg2α= , 24) ctg2α= ,

25) sin3α=3sinα-4sin³α, 26) cos3α=4cos³α-3cosα

27) tg3α= , 28) ctg3α= ,

4.Формули перетворення суми на добуток.

29) sinα+sinβ=2 ,

30) sinα-sinβ=2 ,

31) cosα+cosβ=2 ,

32) cosα-cosβ=-2 ,

33) tgα+tgβ= , 34) tgα-tgβ= ,

35) ctgα ctgβ= ,

36) 1+cos2α=2cos²α, 37) 1-cos2α=2sin²α,

38) cosα sinα= ∙cos(45° α)= ∙sin(45° α),

39) a∙sinα+b∙cosα= , де =arctg ,

40) tgα+ctgα= .

5. Формули перетворення добутку тригонометричних функцій на суму.

41) sinα∙cosβ= (sin(α-β)+sin(α+β)),

42) cosα∙cosβ= (cos(α-β)+cos(α+β)),

43) sinα∙sinβ= (cos(α-β)-cos(α+β)),

6. Формули пониження степеня.

44) sin²α= , 45) cos²α= ,

46) tg²α= , 47) ctg²α= ,

48) cos³α= , 49) sin³α= .

7. Формули «універсальної заміни» (вираження всіх тригонометричних функцій через тангенс половинного аргументу).

50) sinα=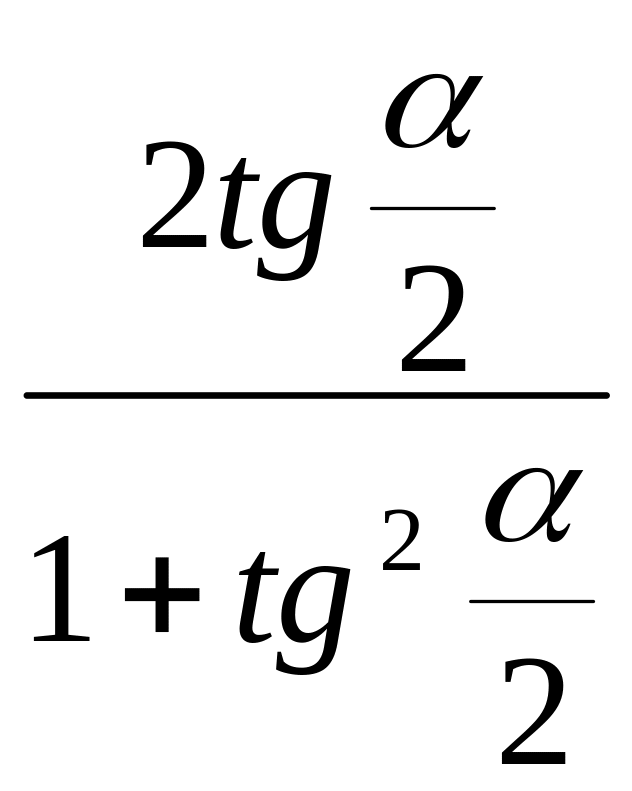 , 51) cosα= ,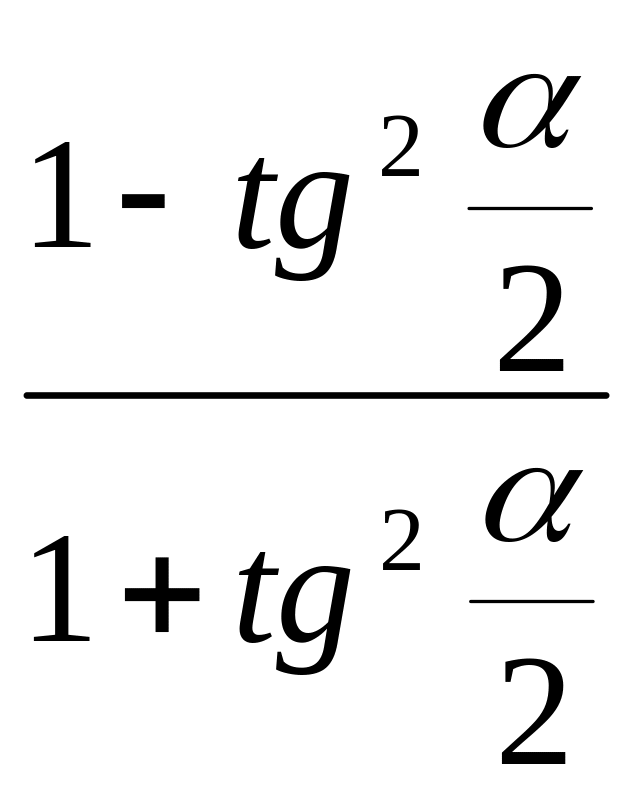

52) tg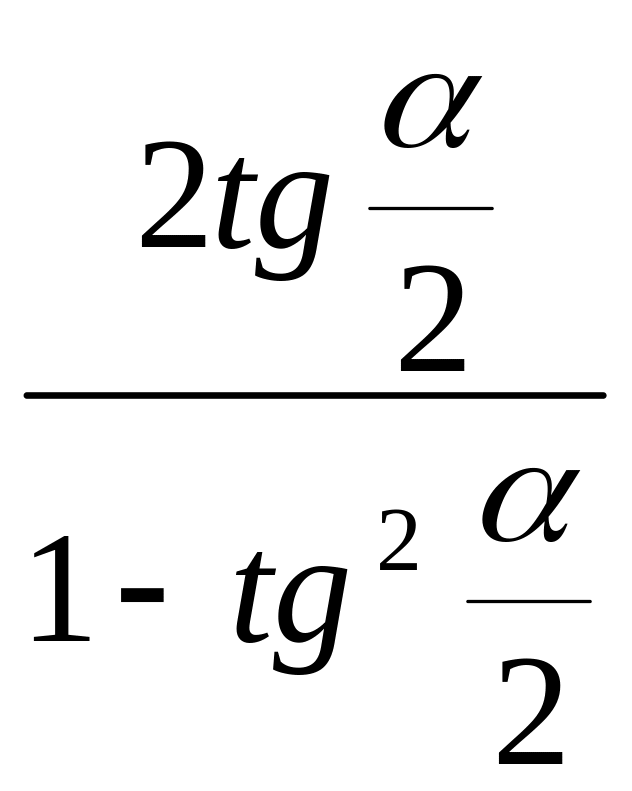α= , 53) ctgα= .

8. Формули половинного аргументу.

54) , 55) ,

56) , 57)

58) , 59) .

9. Формули зведення.

x	sinx	cosx	tgx	ctgx
	cosα	-sinα	-ctgα	-tgα
	-sinα	-cosα	tgα	ctgα
	-cosα	sinα	-ctgα	-tgα
-α	-sinα	cosα	-tgα	-ctgα
	cosα	sinα	ctgα	tgα
	sinα	-cosα	-tgα	-ctgα
	-cosα	-sinα	ctgα	tgα

.Найпростіші тригонометричні рівняння.

Рівняння соsx=a.

1) Якщо , то коренів немає, бо .

2) Якщо , то х=

3) Окремі випадки: cosx=0, тоді x= ,

cosx=1, тоді x=2

cosx=-1, тоді x=

Рівняння sinx=a.

1) Якщо , то коренів немає, бо .

2) Якщо , то х=

3) Окремі випадки: sinx=0, тоді x= ,

sinx=1, тоді x= +2

sinx=-1, тоді x=

Рівняння tgx=a.

1) tgx=a , тоді x=arctga+

2) окремий випадок: tgx=0, тоді x= .

Рівняння сtgx=a.

1) сtgx=a , тоді x=arсctga+

2) окремий випадок: сtgx=0, тоді x= .