4. Дифракція світла Приклади розв’язків задач

Приклад 4.1. Визначити довжину хвилі монохроматичного світла, яке падає нормально на вузьку щілину ширини 50 мкм, якщо напрям на перший максимум дифракції Фраунгофера (по відношенню до початкового напрямку поширення світла) становить 1°00' (див. мал.).

Р озв’язання. Максимуми інтенсивності світла у випадку дифракції Фраунгофера від щілини спостерігають під кутами φ, які задовольняють наближену умову (світло на щілину падає нормально)

,

де m – порядок максимуму.

Знаходимо шукану довжину хвилі (m=1)

.

Відповідь: λ = 580 нм.

П риклад 4.2. На щілину ширини а = 240 мкм падає нормально монохроматичне світло довжини хвилі λ = 600 нм. Дифракційну картину проектують на екран, паралельний до площини щілини, за допомогою лінзи (див. мал.). Визначити відстань від екрану до лінзи, якщо відстань b між першими дифракційними мінімумами, розташованими по обидві сторони від центрального максимуму, дорівнює 10 мм.

Розв’язання. Умова спостереження мінімумів дифракції Фраунгофера від щілини (світло падає нормально)

(1)

де за умовою задачі т=1. З малюнка видно, що , де φ — кут, під яким спостерігають перший мінімум інтенсивності дифрагованого світла. Оскільки , то .

Підставивши останній вираз у формулу (1), отримаємо шукану відстань від екрану до лінзи

Відповідь: l = 2,0 м.

Приклад 4.3. На вузьку щілину падає нормально монохроматичне світло. Визначити напрям на другу темну дифракційну смугу, якщо на ширині щілини укладається 100 довжин хвиль, а екран розміщений у далекій області.

Розв’язання. Тут має місце дифракція Фраунгофера. Умова спостереження мінімумів дифракції Фраунгофера від щілини, на яку світло падає нормально

,

де за умовою задачі т=2. Тоді

.

Оскільки , то шуканий напрям на другу темну дифракційну смугу

.

Відповідь: φ = 1°15'.

П риклад 4.4. На щілину падає нормально паралельний пучок монохроматичного світла. Дифракційну картину проектують на екран за допомогою лінзи, фокусна відстань якої f=50 см. Ширина центральної світлої смуги b=50 мм (див. мал.). Як слід змінити ширину щілини, щоб центральна смуга займала весь екран (за будь-якої ширини екрану).

Розв’язання. Тут має місце дифракція Фраунгофера. Центральна світла смуга розміщена між двома мінімумами першого порядку (див. мал.). Її ширина b залежить від кута дифракції φ, який відповідає напрямку спостереження на перший мінімум. Умова спостереження мінімумів дифракції Фраунгофера від щілини, на яку світло падає нормально

, (1)

де за умовою задачі т=1. У випадку зміни ширини щілині від а₁ до а₂ за незмінних т і λ отримуємо

. (2)

У першому випадку . Щоб центральна смуга зайняла весь екран (за будь-якої ширині екрану), необхідно щоб . Із (2) знаходимо шукане відношення:

.

Відповідь: , тобто ширину щілини слід зменшити у 20 разів.

Приклад 4.5. На дифракційну решітку, яка містить N=200 штрихів на l=1,0 мм, нормально до її поверхні падає монохроматичне світло довжини хвилі λ=500 нм. Поблизу решітки поміщена збиральна лінза, у фокальній площині якої розташований екран, на який проектується картина дифракції. Яка відстань L екрану від лінзи, якщо перший головний максимум дифракції спостерігають на відстані b = 10 см від центрального.

Розв’язання. Умова спостереження головного максимуму дифракції Фраунгофера на решітці.

, (1)

де т — порядок максимуму (за умовою задачі, т=1).

З малюнка видно, що . Оскільки b<<L, то , звідки . Період дифракційної решітки . Підставивши два останні вирази у формулу (1), отримуємо

,

звідки шукана відстань від екрану до лінзи

.

Відповідь: L = 1 м. До речі, ця відстань L = F — фокусні відстані лінзи, яка проектує картину дифракції на екран.

Приклад 4.6. На дифракційну решітку нормально до її поверхні падає пучок монохроматичного світла довжини хвилі λ = 550 нм. Картину дифракції проектують на екран, який розміщений від лінзи на відстані L = 1,0 м, до того ж перший головний максимум спостерігають на відстані l=12 см від центрального. Визначити:

1) період дифракційної решітки;

2) кількість штрихів на 1,0 см її довжини;

3) загальну кількість максимумів, які формує решітка;

4) кут дифракції, який відповідає останньому максимуму.

Розв’язання. 1) Період дифракційної решітки знайдемо з умови спостереження головного максимуму

_{, (1)}

де т — порядок спектру (за умовою задачі, т=1).

З малюнка видно, що . Оскільки l<<L, то . Тоді вираз (1) можна подати у вигляді

,

звідки

2) Кількість штрихів на l'=1,0 см:

.

3) Оскільки найбільший кут відхилення світла решіткою не може перевищувати , з умови (1) можна знайти максимальне значення m

(вважали sinφ_max=1). Природно, що кількість штрихів m повинна бути натуральним числом. Загальна кількість максимумів, які формує дифракційна решітка

,

оскільки максимуми спостерігаються як справа, так і зліва від центрального максимуму (одиниця враховує центральний максимум).

4) Кути дифракції, які відповідають останнім максимумам, знайдемо, подавши умову (1)у вигляді

звідки,

.

Відповідь: 1) d = 4,6 мкм; 2) п = 2,18·10^–3 см^–1; 3) N = 17; 4) φ_max = ±74°.

Приклад 4.7. Монохроматичне світло (λ = 500 нм) падає на дифракційну решітку нормально Найбільший порядок спектру, який спостерігають за допомогою дифракційної решітки, дорівнює 5. Який період дифракційної решітки?

Розв’язання. Умова спостереження головного максимуму дифракції Фраунгофера на решітці:

. (1)

Для визначення максимального числа спостережуваних максимумів слід прийняти до уваги, що максимальний кут дифракції становить (тоді sinφ_max=1). З формули (1) отримуємо (m – ціле число)

,

звідки період дифракційної решітки

Відповідь: d = 2,5 мкм.

П риклад 4.8. Світло довжини хвилі λ = 530 нм падає на прозору дифракційну решітку з періодом d = 1,50 мкм. Знайти кут з нормаллю до решітки, під яким спостерігають головний максимум дифракції Фраунгофера найбільшого порядку, якщо кут падіння світла на решітку θ₀ = 60°.

Розв’язання. Максимуму найбільшого порядку повинна відповідати максимальна різниця ходу Δ між відповідними променями 1 і 2 від сусідніх щілин, як зображено на мал. 5.41. Для цього необхідно, щоб

. (1)

Спочатку знайдемо максимальне значення т. З огляду на те, що θ_m не може перевищувати π/2, покладемо sinθ_m=1. Тоді

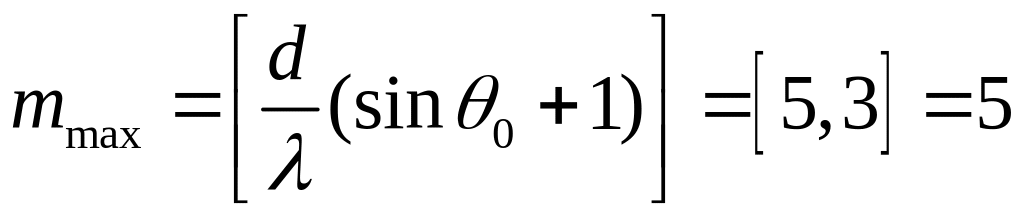, (2)

де квадратні дужки означають, що від отриманого кількістьвого значення треба взяти цілу частина.

Залишається підставити т_макс в (1), і ми одержимо:

.

Звідки θ_m = 64°.

Приклад 4.9. Світло довжини хвилі λ = 535 нм падає нормально на прозору дифракційну решітку. Знайти її період, якщо один із максимумів дифракції Фраунгофера виникає під кутом дифракції δ_т = 35°, а найбільший порядок спостережуваних максимумів дорівнює п'ять.

Розв’язання. Запишемо умови спостереження головних максимумів дифракції Фраунгофера на решітці:

, (1)

. (2)

Із цих формул одержимо

. (3)

Для обрахунку т необхідно, щоб значення sinθ_макс було якнайближчим до одиниці, але таким, щоб т при цьому було цілим. Це буде, як неважко встановити, коли sinθ_Макс = 0,955. Тоді т=3, і з формули (1) знайдемо шуканий період:

.

Відповідь: d = 2,8 мкм.

Приклад 4.10. Паралельний пучок монохроматичного Х-випромінювання (λ = 243 пм) падає під кутом ковзання θ = 60° на природну грань кристалу кам'яної солі. Внаслідок дзеркального відбивання від цієї грані спостерігають максимум дифракції Фраунгофера другого порядку. Яка відстань d між атомними площинами кристалу?

Розв’язання. Напрями спостереження максимумів дифракції від кристалічної решітки (в даному випадку кристалу кам'яної солі) визначає формула Вульфа-Брегга:

,

де d — відстань між атомними площинами кристалу; θ — кут ковзання (кут між напрямом падаючого випромінювання і гранню кристалу); λ — довжина хвилі Х-випромінювання; т — порядок максимуму. Тоді шукана відстань між атомними площинами кристалу – період ідентичності

Відповідь: d = 2,810^–10 м = 2,8 Å.

П риклад 4.11. Вузький пучок Х-випромінюванння довжини хвилі λ падає під кутом ковзання α = 60° на природну грань монокристала NaCl, густина якого ρ = 2,16 г/см³. Внаслідок дзеркального відбивання від цієї грані спостерігають максимум дифракції другого порядку (т = 2). Визначити λ.

Розв’язання. Відповідно до формули Брегга-Вульфа (5.36)

.

Як видно, розв’язування задачі зводиться до знаходження міжплощинної відстані (періоду ідентичності кристалу) d. Остання дорівнює довжині ребра елементарної кубічної комірки, у вузлах якої почергово перебувають іони Na⁺ і С1^– (мал. 5.42). На таку комірку від кожного іона припадає 1/8 частина. Отже, на всю комірку припадає 4∙(1/8) = 1/2 іона Na⁺ і 1/2 іона С1^–. Тобто маса М, що припадає на об’єм d³, дорівнює половині маси М_М молекули NaCl: M=М_м/2.

Густина — це відношення маси, що припадає на кожну комірку, до її об'єму: ρ = M/d³ . Звідси

.

У результаті одержимо:

пм = 2,4 Å.