Мотс. Задание № 3. Вариант № 10.

²

Дан функционал I(x)=t²x²dtэкстр

₁

₂

_{Ограничения} txdt =7/3 ,x(1)=1,x(2)=2

1

Найти х(t)

Решение:

1.Составляем функцию Лагранжа:

f = t²x² -подинтегральное выражение функционала,

k= tx- подинтегральная функция ограничения

L= f+k = t²x² +tx

2 Подставляем L в формулу Эйлера:

L_x – d/dt(L_x)=0 , где L_х =t, L_x=2xt²

Следовательно получим уравнение :

t– d/dt(2xt²)=0

3. Рещаем диффернциальное уравнение

d(2xt²)= tdt

2xt² =t²/2+C₁

x= /4+C₁/( 2t²)

x = t/4 - C₁/( 2t) +C₂

Для нахождения С1,С2 и  воспользуемся ограничениями :

2

txdt=7/3 ,x(1)=1,x(2)=2

Тогда : 1= /4- C₁/2+С₂

2= /2- C₁/4+С₂

Откуда : С₁= 4-, С₂=3-3/4

Выразим х через : х =t/4 + /(2t) –2/t +(3-3/4)

Подставим х в ограничение вида :

2

txdt=7/3

1

Тогда :

2

t²/4+ /2 –2 + t(3-3/4) dt=7/3 , вычисляем интеграл:

1

2 2 2

t³/12 + (3-3/4)t²/2 + (/2 –2)t =2,5-/24=7/3

1 1 1

След-но =4

Подставив =4 в выражение для С₁ иС₂ получим С₁=С₂=0

Тогда х = t/4 = t

Ответ : x = t

Мотс. Задание № 4. Вариант № 10.

Дан объект второго порядка, имеющий два нулевых корня. Найти оптимальное по быстродействию управление, при котором объект из любой точки фазовой плоскости переходил бы в начало координат за минимальное время.

u = d²y/dt² , u  1, y₁₀(0)= -1.7 , y₂₀(0)= -1.2 , y_1к(T)= 0 , y_2к(T)= 0 .

Решение

1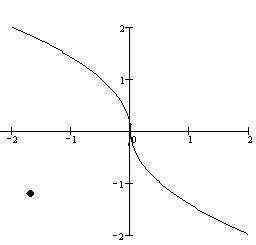 .Определим первоначальное управление.

Построим начальную точку на фазовой плоскости

начальная точка находиться ниже кривой переключения, следовательно, первоначальное управление u=1, после переключения u=-1.

2 .Находим начальную и конечную траекторию движения.

Для рассматриваемого случая начальная траектория y₁ = 0,5 y₂² + S₁ ,

конечная траектория y₁ = -0,5 y₂².

3.Подставляем координаты начальной точки y₁(0)= y₁₀ , y₂(0)= y₂₀ , в уравнения для фазовых координат при управлении и = 1 , находим постоянные К₁ , К₂ , S₁ :

y₂ = t + К₁ ,

y₁ = t²/2 + К₁ t + К₂ = 0,5 y₂² + S₁ ,

y₂₀ = 0 + К₁ ,

y₁₀ = 0 + 0 + К₂ ,

y₁₀ = 0,5 y₂₀² + S₁ , S₁= y₁₀ + 0,5 y₂₀²

y₁₀ =-1.7 y₂₀ = -1.2 К ₁=-1.2 К₂ = -1.7 S₁ =-2.425

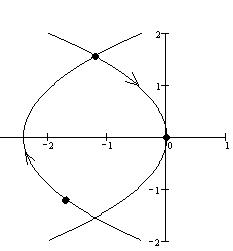
4. Нахождение времени переключения. Для этого используем равенство y₁ = -0,5 y₂² (уравнение линии переключения) :

t_п²/2 + К₁t_п + К₂ = -0,5 (t_п + К₁ )²

t_п = 2.756

5. Находим координаты точки переключения:

y_1п = t_п²/2 + К₁ t_п + К₂ ,

y_2п = t_п + К₁

y_1п = -1.21 y_2п = 1.556

6. Находим коэффициенты А₁ и А₂ , решив систему уравнений:

y_1п = - t_п²/2 + А₁t_п + А₂ ,

y_2п = - t_п + А₁

А₁ = 4.311

А₂ = -9.294

7. Находим время прихода в конечную точку из уравнения:

y_2к = 0 = -t_к + А₁ , t_к = А₁

t_к = 4.311

Оптимальная траектория движения изображена