
Пермский Государственный Технический Университет
Кафедра АТ
Контрольная работа.
Математические основы теории систем.
Вариант № 10.
Выполнил: студент гр.
Проверил:
г. Пермь 20012 г.
Мотс. Вариант № 10. Мотс. Задание № 1. Вариант № 10.
Решение ЗЛП
Вариант № 10
Задача: Q = X1 + X2 max,
X1 – X2 >= -1,
X1 – X2 <= 1,
X1 <= 2,
X2 <= 2,
X1, X2 >= 0.
Графический способ решения
Способ 1.
Заменяем ограничения-неравенства ограничениями-равенствами:
X1 – X2 = -1,
X1 – X2 = 1,
X1 = 2,
X2 = 2,
X1 = X2 = 0.
Строим графики полученных функций (рис. 1)
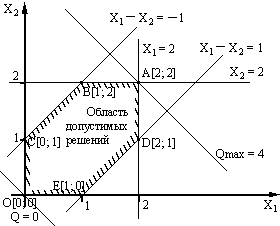
рис. 1.
Находим область допустимых решений (область, где выполняются все ограничения).
Строим график целевой функции при каком-либо значении правой части:
Q = X1 + X2 = 0,
X2 = - X1.
График целевой функции перемещаем параллельно его начальному положению в сторону роста целевой функции до касания с границей области допустимых решений.
Граничная точка является решением задачи.
Ответ: А[2, 2], Qmax = 4.
Способ 2.
Пункты 1 – 3 выполняются так же как в способе 1.
4. Подсчитываем значения целевой функции во всех вершинах допустимого прямоугольника и выбираем максимальное значение:
O[0, 0], Q = 0,
A[2, 2], Q = 4,
B[1, 2], Q = 3,
C[0, 1], Q = 1,
D[2, 1], Q = 3,
E[1, 0], Q = 1.
Максимальное значение целевой функции Qmax = 4, следовательно, точка A[2, 2] – решение задачи.
Ответ: A[2, 2], Qmax = 4, что совпадает с ответом, полученным в способе 1.
Симплекс-метод решения задачи.
Приводим задачу к каноническому виду путем введения искусственных переменных и умножения целевой функции на -1:
-X1 + X2 + X3 = 1,
X1 – X2 + X4 = 1,
X1 + X5 = 2,
X2 + X6 = 2.
G = - X1 - X2 min
Составляем симплекс-стаблицу:
-
1 2
3
4
5
6
-1 1
1 -1
1 0
0 1
1
1
2
2
-1 -1
0
В качестве разрешающего столбца симплекс-таблицы выберем тот, который соответствует свободной переменной Х2. (Можно выбрать и Х1, разницы нет, так как коэффициенты целевой функции равны).
Для выбора разрешающей строки надо найти отношение правых частей ограничений к положительным коэффициентам разрешающего столбца, где получится меньше – там и будет разрешающая строка:
Для Х3 - 1/1=1,
Для Х6 - 2/1=2.
Разрешающая строка соответствует базисной переменной Х3.
Элемент, стоящий на пересечении разрешающей строки и разрешающего столбца, это разрешающий элемент симплекс-таблицы (здесь и далее выделен цветом).
Выбранные свободная и базисная переменные (находящиеся в разрешающих строке и столбце соответственно) меняются местами в симплекс-таблице.
Коэффициенты симплекс-таблицы пересчитываются:
Разрешающий элемент равен 1.
Новый разрешающий элемент равен единице, деленной на старый разрешающий элемент: 1/1=1,
Элементы новой разрешающей строки, находят как произведение пересчитанного разрешающего элемента на соответствующие элементы старой разрешающей строки:
-1*1=1, 1*1=1,
Новый разрешающий столбец равен произведению элементов старого разрешающего столбца и пересчитанного разрешающего элемента, взятого с обратным знаком:
-1*(-1)=1, 0*(-1)=0, 1*(-1)=-1, -1*(-1)=1,
Для нахождения элементов других столбцов надо из старого столбца вычесть произведение элемента, уже стоящего в новом столбце, и старого разрешающего столбца:
-
1
1
0
-1
+1*
-1
0
1
-1
=
0
1
1
-2
-
1
2
2
0
- 1*
-1
0
1
-1
=
2
2
1
1
Новая симплекс-таблица имеет вид:
-
1 3
2
4
5
6
-1 1
0 1
1 0
1 -1
1
2
2
1
-2 1
1
По данным таблицы:
Х1=Х3=0, Х2=1, Х4=2, Х5=2, Х6=1, G=-1, Q=1.
Проверка вычислений:
-X1 + X2 + X3 = 1, -0+1+0=1,
X1 – X2 + X4 = 1, 0 –1+2=1,
X1 + X5 = 2, 0+2=2,
X2 + X6 = 2. 1+1=2,
G=-X1-X2, -0-1=-1,
Q=X1+X2. 0+1=1.
Проверка сошлась, значит вычисления были проведены верно.
Как видим полученная вершина не оптимальна и требуется перейти к следующей вершине.
Новый разрешающий столбец соответствует свободной переменной Х1 (так как максимальный по модулю отрицательный коэффициент целевой функции равен –2).
Для выбора разрешающей строки надо найти отношение правых частей ограничений к положительным коэффициентам разрешающего столбца, где получится меньше – там и будет разрешающая строка:
Для Х5 - 2/1=2,
Для Х6 - 1/1=1.
Разрешающая строка соответствует базисной переменной Х6.
Далее считаем по вышеизложенному алгоритму:
Разрешающий элемент равен 1.
Новый разрешающий элемент: 1/1=1,
Элементы новой разрешающей строки: -1*1=1, 1*1=1,
Новый разрешающий столбец: -1*(-1)=1, 0*(-1)=0, 1*(-1)=-1, -2*(-1)=2,
Элементы других столбцов:
-
1
1
0
1
+1*
-1
0
1
-2
=
0
1
1
-1
-
1
2
2
1
- 1*
-1
0
1
-2
=
2
2
1
3
Новая симплекс-таблица имеет вид:
-
6 3
2
4
5
1
1 0
0 1
-1 1
1 -1
2
2
1
1
2 -1
3
Х1=1, Х2=2, Х3=Х6=0, Х4=2, Х5=1, G=-3, Q=3.
Проверка вычислений:
-X1 + X2 + X3 = 1, -1+2+0=1,
X1 – X2 + X4 = 1, 1 –2+2=1,
X1 + X5 = 2, 1+1=2,
X2 + X6 = 2. 2+0=2,
G=-X1-X2, -1-2=3,
Q=X1+X2. 1+2=3.
Проверка сошлась, значит вычисления были проведены верно.
Полученная вершина опять не оптимальна и требуется перейти к следующей вершине.
Новый разрешающий столбец соответствует свободной переменной Х3 (так как максимальный по модулю отрицательный коэффициент целевой функции равен –1).
Для выбора разрешающей строки надо найти отношение правых частей ограничений к положительным коэффициентам разрешающего столбца, где получится меньше – там и будет разрешающая строка:
Для Х4 - 2/1=2,
Для Х5 - 1/1=1.
Разрешающая строка соответствует базисной переменной Х4.
Далее считаем по вышеизложенному алгоритму:
Разрешающий элемент равен 1.
Новый разрешающий элемент: 1/1=1,
Элементы новой разрешающей строки: -1*1=1, 1*1=1,
Новый разрешающий столбец: 0*(-1)=0, 1*(-1)=-1, -1*(-1)=1, -1*(-1)=1,
Элементы других столбцов:
-
1
0
1
2
+1*
0
1
-1
-1
=
1
1
0
1
-
2
2
1
3
- 1*
0
1
-1
-1
=
2
1
2
4
Новая симплекс-таблица имеет вид:
-
6 5
2
4
3
1
1 0
1 -1
-1 1
0 1
2
1
1
2
1 1
4
Х1=1, Х2=1, Х3=1, Х4=1, Х5=Х6=0, G=-4, Q=4.
Проверка вычислений:
-X1 + X2 + X3 = 1, -2+2+1=1,
X1 – X2 + X4 = 1, 2–2+1=1,
X1 + X5 = 2, 2+0=2,
X2 + X6 = 2. 2+0=2,
G=-X1-X2, -2-2=-4,
Q=X1+X2. 2+2=4.
Проверка сошлась, значит, вычисления были проведены верно.
Все коэффициенты целевой функции положительны, следовательно, найдено оптимальное и единственное решение задачи.
Ответ: координаты вершины (Х1=1, Х2=1, Х3=1, Х4=1, Х5=Х6=0), Gmin=-4, Qmax=4.
