Розділ 1. Механіка

ЛАБОРАТОРНА РОБОТА № 10

«Визначення моментів інерції кулі і циліндра»

Мета роботи: навчитись визначати моменти інерції кулі та циліндра, перевірити рівняння динаміки обертального руху.

Завдання:

1. Визначити момент інерції кулі.

2. Визначити момент інерції циліндра

Обладнання та інструменти: динамометр, лінійка, штатив з муфтою і лапкою, наклонний жолоб, кулька, циліндр, лоток з піском.

Вказівки на теоретичний матеріал:

1. Динаміка обертального руху. Основне рівняння.

2. Момент інерції. Теорема Штейнера.

Теоретичні положення

Момент інерції — скалярна фізична величина, міра інертності тіла в обертальному русі довкола осі, подібно до того, як маса тіла є мірою його інертності в поступальній ході. Характеризується розподілом мас в тілі: момент інерції дорівнює сумі добутків елементарних мас на квадрат їх відстаней до базової множини (точки, прямої або площини).

Одиниця виміру СІ: кг·м². Позначення: I або J.

Теорема Штейнера

Момент інерції твердого тіла відносно якої-небудь осі залежить не лише від маси, форми і розмірів тіла, але також від положення тіла по відношенню до цієї осі.

І = І₀ + mа² (1)

де І₀ – момент інерції тіла відносно центра мас,

а – відстань від осі обертання до центра мас тіла,

І – момент інерції тіла відносно осі обертання.

Моменти інерції однорідних тіл простої форми відносно деяких осей вращенія

Тіло	Опис	Положення осі а	Момент інерції І0
	Матеріальна точка маси m	На відстані r від крапки, нерухома
	Порожнистий тонкостінний циліндр або кільце радіусу r і маси m	Вісь циліндра
	Суцільний циліндр або диск радіусу r і маси m	Вісь циліндра
	Порожнистий товстостінний циліндр маси m із зовнішнім радіусом r2 і внутрішнім радіусом r1	Вісь циліндра
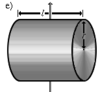
	Суцільний циліндр довжини l, радіусу r і маси m	Вісь перпендикулярна до циліндра і проходить через його центр мас
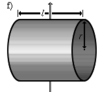
	Порожнистий тонкостінний циліндр (кільце) довжини l, радіусу r і маси m	Вісь перпендикулярна до циліндра і проходить через його центр мас
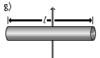
	Прямий тонкий стрижень довжини l і маси m	Вісь перпендикулярна до стрижня і проходить через його центр мас
	Прямий тонкий стрижень довжини l і маси m	Вісь перпендикулярна до стрижня і проходить через його кінець
	Тонкостінна сфера радіусу r і маси m	Вісь проходить через центр сфери
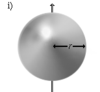
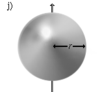
	Шар радіусу r і маси m	Вісь проходить через центр кулі
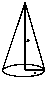
	Конус радіусу r і маси m	Вісь конуса
	Рівнобедрений трикутник з висотою h, підставою а і масою m	Вісь перпендикулярна плоскості трикутника і проходіт через вершну
	Правильний трикутник із стороною а і масою m	Вісь перпендикулярна плоскості трикутника і проходить через центр мас
	Квадрат із стороною а і масою m	Вісь перпендикулярна плоскості квадрата і проходить через центр мас

Закон збереження і перетворення енергії:

Енергія не виникає і не зникає: вона лише переходить з одного виду в інший.

Механічна енергія тіла – сума кінетичної і потенціальної енергій тіла

Е = Е_к + Е_п (2)

Закон збереження і перетворення механічної енергії:

Повна механічна енергія замкненої системи тіл, які взаємодіють силами тяжіння і пружності, залишається незмінною за будь-яких взаємодій тіл між собою.

Кінетична енергія – енергія рухомого тіла.

(3)

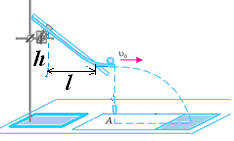
Рисунок 1.

По похилій площині тіло рухається рівноприскорено, причому збільшується як лінійна, так і циклічна швидкості: (4) (5) (6) (7)

Потенціальна енергія кульки в початковий момент:

E_п = mgh (8)

Закон збереження енергії:

Е_п = Е_к1 + Е_к2 (9)

Використовуючи формули (3) – (9) запишемо формулу для розрахунку моменту інерції тіла:

(10)

Момент інерції кулі:

(11)

Момент інерції циліндра:

(12)

Похибки вимірювань розраховують так:

(13)

де абсолютні похибки вимірювань маси, відстані, часу і радіуса знаходяться з формули:

(14)

 - похибка приладу; ν - похибка відліку, .