2. Вказівки з використанНя літературних джерел

До розділу 5:

1. С. Гудман, С. Хидетниеми. Введение в разработку и анализ алгоритмов.- Москва: Мир, 1981. – 366 с.

Розглядаються етапи побудови алгоритму, матоди розробки алгоритмів, методи оцінок алгоритмів та деякі структури даних: списки, черги, стеки, дерева тощо.

2. Роберт Седжвик. Фундаментальные алогоритмы на С, 3 редакция. - Киев: издательство «DiaSoft», 2003г.- 1127с.

Розглядаються принципи аналізу алгоритмів, рекурсіі, структури даних: масиви, дерева, рядки, списки, метода сортування, хешування та хеш-функції.

3. Кормен «Алгоритми: побудова та аналіз»

В даних книгах розгладаються структури даних, етапи розробки алгоритмів, наведена велика кількість прикладів.

До розділу 6:

1) Марков А.А., Нагорный Н.М. Теория алгоритмов. -М.: Наука, 1984.- 420с.

2) Мальцев А.И. Алгоритмы и рекурсивные функции. -М.: Наука, 1986. 320с.

До розділу 7:

1) Гери М., Джонсон Д. Вычислительные машины и труднорешаемые задачи. - М.: Мир, 1982.-420с.

2) Катленд Н. Вычислимость. - М.: Мир, 1983.-180с.

До розділу 8:

1) Ющенко К.Л., Суржко С.В., Цейтлин Г.О., Шевченко А.І. Алгоритмічні алгебри: Навч.посібник. - К.:ІЗМН, 1997. - 480 с.

2) Глушков В.М., Цейтлин Г.Е., Ющенко Е.Л. Алгебра. Языки. Программирование. - К.: Наукова думка, 1984.-360с.

ВПРАВИ

(без зірочки) - година виконання задачі 5-20 хв.

* - задачі підвищеної складності (45-60 хв.)

^п – задачі для програмування

Алгоритми й структури даних

1. Кодування-декодування. Один елементарний шифр складається з того, щоб поставити букви алфавіту до взаємно-однозначної відповідності з буквами відсортованого алфавіту. Наприклад:

   1. Алфавіт: ABCDEFGHIJKLMNOPQRSTUVWXYZ

   2. Букви коду : MTJCZEOKLNSUXYADFBWVG H I P R Q, тоді слово CODE буде зашифроване як JACS.

2. Побудуйте, перевірте, та оформіть документацією алгоритм, для якого код є уведенням та який кодує та декодує будь-які запису.

3. Для довільної трійки чисел (х, в, z) повністю побудувати алгоритм, що визначає, чи існує трикутник зі сторонами х, в, z.

4. Алгебра складності.

   1. Покажіть, що f(n)=3.7n²+100.8n+10 має порядок ПРО(n²) при n→∞.

   2. Покажіть, що f(n)= 2ⁿ/100—100 має порядок ПРО(2") при n→∞.

   3. Покажіть, n! має порядок ПРО(nⁿ) при n→∞.

   4. Покажіть, що 2ⁿ зростає при n→∞ швидше, ніж будь-який поліном від n обмеженого ступеня.

5. Побудуйте алгоритм, що перетворює будь-яку додатне ціле число, що записане в арабських числах, до системи римських чисел та навпаки.

6. Розробіть два різних алгоритми для генерації випадкових перестановок. Порівняйте їх ефективність.

7. Розробіть алгоритм, що обчислює значення функції F(n)=m, де n-кількість знаків, що містяться в десятковому записі n!.

8. Відомо, що година виконання одному алгоритму дорівнює O(N log), а година виконання іншого алгоритму дорівнює O(N³). Що можна сказати про відносну ефективність даних алгоритмів?

9. Відомо, що година виконання одному алгоритму приблизно дорівнює N log, а година виконання іншого алгоритму приблизно дорівнює N³ . Що можна сказати про відносну ефективність даних алгоритмів?

10. Відомо, що година виконання одному алгоритму приблизно дорівнює N log, а година виконання іншого алгоритму дорівнює O(N³). . Що можна сказати про відносну ефективність даних алгоритмів?

11. Відомо, що година виконання одному алгоритму завжди пропорційний N log, а година виконання іншого алгоритму завжди пропорційний N³. Що можна сказати про відносну ефективність даних алгоритмів.

12. Відсортувати задану послідовність чисел вказаним методом, пояснити послідовність кроків алгоритму та оцінити година роботи алгоритму:

    1. Проста вставка

    2. методом Шелла

    3. швидке сортування Хоару

    4. пірамідальне сортування

    5. природне двошляхове злиття

    6. фіксоване двошляхове злиття

    7. порівняння й підрахунок

    8. розподільний підрахунок

    9. бінарне сортування (метод ділення відрізку навпіл)

13. * Задача комівояжера. Знайдіть оптимальне рішення задачі комівояжера, зображеній на малюнку, застосувавши алгоритм ETS.

14. 

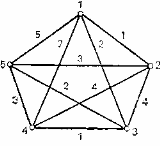
15. * Побудуйте алгоритм, що генерує всі перестановки перших n цілих додатних чисел. Чи підходить ваш алгоритм до кроку 2 алгоритму ETS?

16. * Побудуйте під алгоритм для побудови турів до кроку 3 алгоритму ETS.

17. * Розглянемо матрицю коштів Із задачі комівояжера з n містами. Якщо мі візьмемо n елементів з Із таким чином, що лише один елемент буде вибрано з шкірного рядка та стовпчика, чи будуть відрізки шляху, що відповідають елементам, утворювати тур?