8.3 Кездейсоқ шамалар

Кездейсоқ шама деп тәжірибе нәтижесінде алдын ала белгісіз және көптеген себептерге байланысты өзінің мүмкін сандық мәндерінің тек қана біреуін қабылдайтын шаманы айтамыз.

Сонымен, тәжірибе нәтижесінде кездейсоқ оқиғаның пайда болуы немесе пайда болмауы алдын ала белгісіз болса, ал кездейсоқ шама міндетті түрде пайда болады, тек оның қандай мәнді қабылдайтыны алдын ала белгісіз. Мысалы, тиын екі рет лақтырылды. “Цифр” жағының пайда болуы немесе пайда болмауы кездейсоқ оқиға, ал оның пайда болу саны кездейсоқ шама болады. Бұл жағдайда кездейсоқ шаманың мүмкін мәндері 0,1, 2 болады, яғни “цифр” жағы пайда болмайды немесе 1 рет, немесе 2 рет пайда болады.

Кездейсоқ шамалар Х, У, Z, … бас әріптермен, ал оның мүмкін мәндері х, у, z, ... кіші әріптермен белгіленеді. Мысалдар келтірейік.

1. Жаңа туған 100 сәбидің ішіндегі ер балалар саны - кездейсоқ шама, ал оның мүмкін мәндері 0, 1, 2, ..., 100 болады.

2. Зеңбіректен атылған снарядтың ұшу қашықтығы - кездейсоқ шама болады. Ұшу қашықтығы оптикалық көздеуіштің орналасуына, желдің бағытымен жылдамдығына және т.б. көптеген себептерге байланысты. Бұл жағдайда осы шаманың мүмкін мәндері қандай да бір (а, в) аралығында жатады.

3. Тәуелсіз n тәжірибедегі А оқиғасының пайда болу саны - кездейсоқ шама болады, ал оның мүмкін мәндері 0, 1, 2, 3, ... n болады.

Кездейсоқ шамалар дискретті (үзілісті) және үзіліссіз кездейсоқ шамалар болып екіге бөлінеді.

1. Дискретті кездейсоқ шамалар. Х кездейсоқ шамасының қабылдайтын мәндері ақырлы бүтін сандар немесе тізбек түрінде жазылса, онда ол дискретті (үзілісті) кездейсоқ шама деп аталды.

Дискретті Х кездейсоқ шаманың мәндері мен олардың сәйкес ықтималдықтарының арасындағы байланысты дискретті кездейсоқ шаманың үлестірім заңы деп атайды. Ол кесте, график және аналитикалық түрде беріледі. Кесте түрінде былай беріледі:

8.1 Кесте

Х			...
Р			...

мұндағы

Графиктік түрде былай беріледі: ол үшін декарттық координаталар жүйесінде нүктелерін саламыз, мұндағы - кездейсоқ шаманың мүмкін мәндері, ал - сәйкес ықтималдықтары. Егер осы нүктелерді кесінділермен қоссақ, онда пайда болған фигура үлестірім көпмүшесі деп аталады (8.1 Сурет).

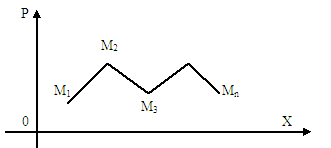
8.1 Сурет

Егер Х кездейсоқ шамасының мүмкін мәндері 0, 1, 2, ... , n болып, оның сәйкес ықтималдығы

Бернулли формуласымен берілсе, онда Х кездейсоқ шамасы Бернулли немесе бином үлестірім заңына бағынады делінеді.

Егер Х кездейсоқ шамасының мүмкін мәндері 0, 1, 2, ... , n, ал n үлкен сан және р ықтималдығының шамасы аз болып, оның сәйкес ықтималдықтары

Пуассон формуласымен берілсе, онда Х кездейсоқ шамасы Пуассон үлестірім заңына бағынады деп аталады.

Егер Х кездейсоқ шамасы 0, 1, 2, ... , n, мәндерін қабылдап, олардың сәйкес ықтималдықтары

формуласымен анықталса, онда Х кездейсоқ шамасы геометриялық үлестірім заңына бағынады деп аталады.

Егер Х кездейсоқ шамасы 0, 1, 2, ... , n мәндерін қабылдап, оның сәйкес ықтималдығы

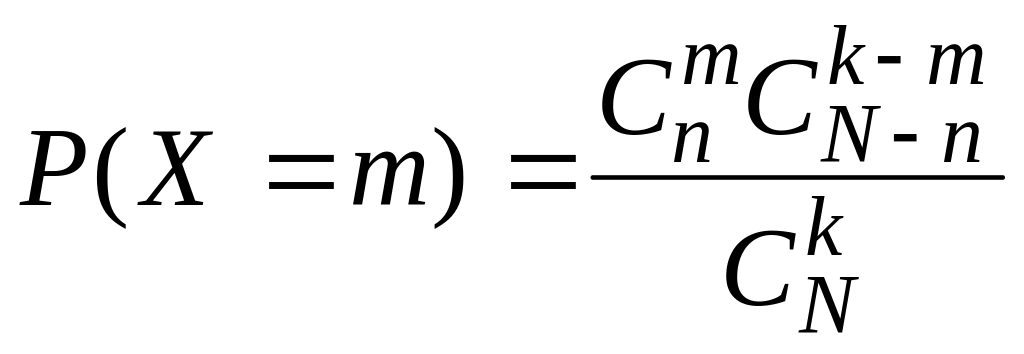
формуласымен анықталса, мұндағы , онда Х кездейсоқ шамасы гипергеометриялық үлестірім заңына бағынады деп аталады.

Егер тәуелсіз екі кездейсоқ шамалардың

8.2 Кесте

Х	х1	х2
Р	р11	р12

8.3 Кесте

У	у1	у2	у3
Р	р21	р22	р23

үлестірім заңдары берілсе, мұндағы онда