7.3 Тейлор және Маклорен қатарлары

функциясы аралығында анықталған және кез келген ретті туындылары бар болсын. Тейлор формуласы бойынша

мұндағы

Егер болса, онда

қатары Тейлор қатары деп аталады. - Тейлор қатарының қалдық мүшесі дейді.

Егер болса, онда Тейлор қатары Маклорен қатары деп аталады да

түрінде жазылады.

Егер функциясы аралығында анықталып, кез келген n үшін теңсіздігі орындалса (мұндағы М-оң тұрақты сан), онда осы функция Тейлор қатарына жіктеледі. Кейбір функциялардың Маклорен қатарына жіктелуін көрсетейік:

1.

2.

3.

4.

5.

6.

Соңғы жіктеуде:

Дербес жағдайда:

а)

ә) болса, онда

б) болса, онда

7.

Жуықтап есептеулерде функциялардың Маклорен қатарларына жіктелуін пайдалану керек. Ал логаримді есептеу үшін кейбір жағдайларда

формуласын пайдаланған тиімді.

654. функциясын х дәрежесі бойынша жіктеу керек.

Шешуі. Берілген функцияның және оның туындыларының нүктесіндегі мәндерін табайық.

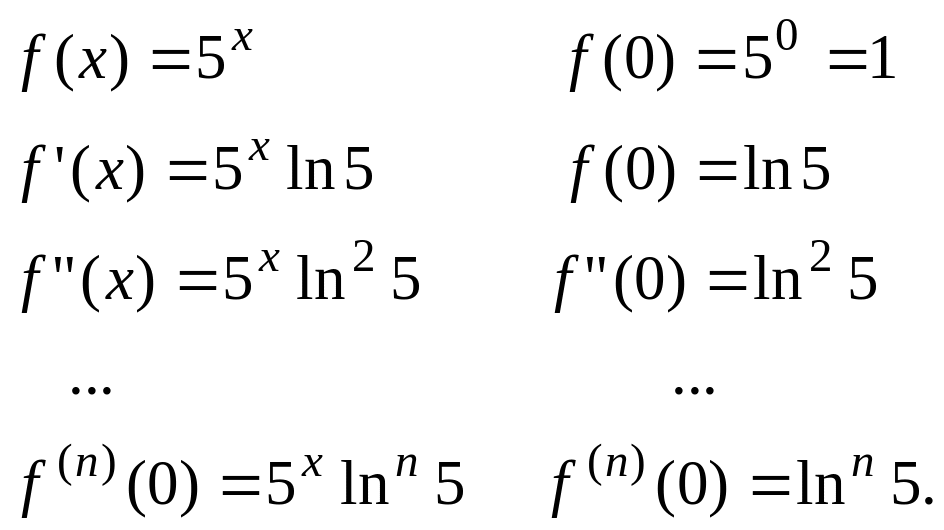
Енді функцияны Маклорен қатарына жіктейік:

.

Бұл функцияны Маклорен қатарына жіктеу үшін белгілі функциясының жіктелуін қолдану арқылы да табуға болады. Ол үшін х-ті өрнегімен ауыстыру керек. ▲

655. функциясының х дәрежесі бойынша жіктеу керек.

Шешуі. функциясының жіктелуін пайдаланып, х-тің орнына алсақ, онда ▲

656. функциясын х дәрежесі бойынша жіктеу керек.

Шешуі. болғандықтан болады, осыдан . ▲

657. функциясын Маклорен қатарына жіктеу керек.

Шешуі. теңдігін және функциясының жіктелуін қолдансақ, онда .

Бұл қатар аралығында жинақты болады. ▲

658. функциясын Маклорен қатарына жіктеу керек.

Шешуі. теңдігін және функциясының жіктелуін қолданып, х-тің орнына -ті алмастырсақ, онда

. ▲

659. функциясын Маклорен қатарына жіктеу керек.

Шешуі. болғандықтан Мұндағы Сондықтан функциясының жіктелуін пайдалансақ:

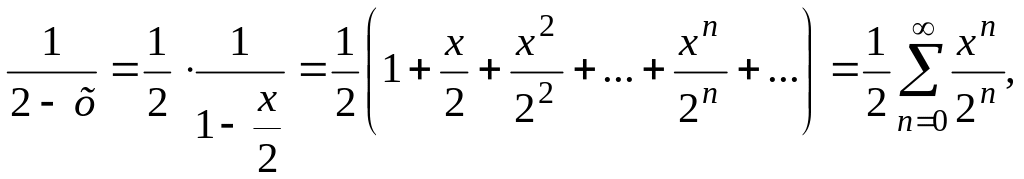
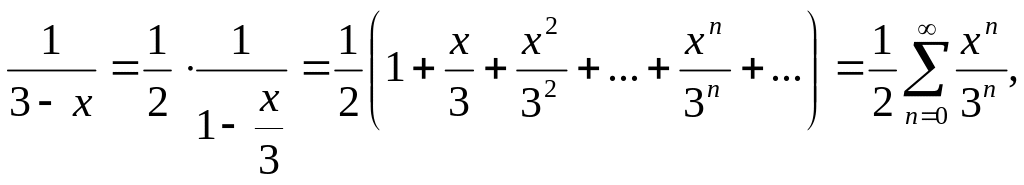
яғни ▲

660. функциясын дәрежесі бойынша жіктеу керек.

Шешуі. деп алсақ, онда Осы функцияға функциясының жіктелуін қолдансақ,

Осыдан

. ▲

661. е санын 0,0001 дәлдікпен есептеу керек.

Шешуі. функциясының жіктелуін қолданамыз. Онда болғанда болады. n санын жуық мәнінің қатесі 0,0001 дәлдікпен аспайтындай етіп, таңдап алуымыз керек. болғандықтан мұндағы

Егер болса, онда

Егер болса, онда

яғни ▲

662. санын 0,0001 дәлдікпен есептеу керек.

Шешуі. функциясының жіктелуін қолдансақ

,

Бұл жағдайда екі мүшесін алу керек, себебі яғни ▲

663. санын 0,0001 дәлдікпен есептеу керек.

Шешуі. 528 санына жақын бүтін санның кубы болып табылады, сондықтан 528 санын қосындысы түрінде жазуға болады. Олай болса,

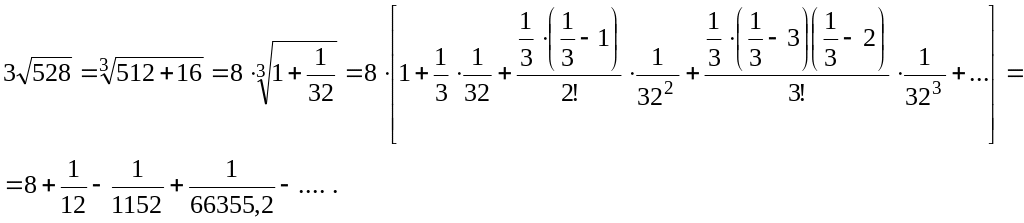Төртінші мүше 0,0001 санынан кіші болғандықтан алғашқы үш мүшелерінің қосындысын аламыз, сондықтан ▲

664. шегін табу керек.

Шешуі. функциясының Маклорен қатарын қолдансақ, онда

▲

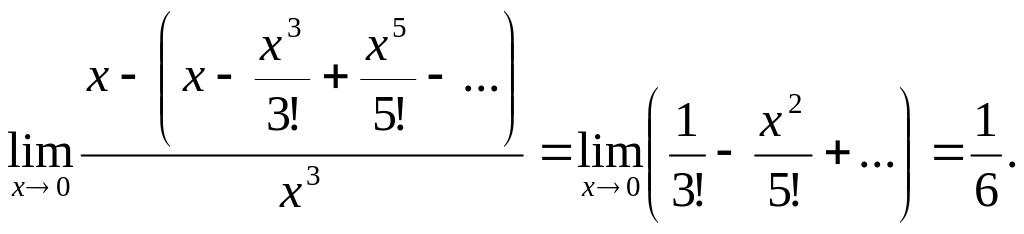665. интегралын 0,001 дәлдікпен есептеу керек.

Шешуі. функциясының жіктелуін пайдалана отырып, қатарын аламыз. Осыдан

Үшінші мүшесі 0,001 санынан кіші болғандықтан, алғашқы екі мүшесін алсақ жеткілікті ▲

Келесі функцияларды х-тің дәрежесі бойынша қатарға жіктеу керек.

666. Ж:

667. Ж:

668. Ж:

669. Ж:

670. Ж: .

671. Ж: .

672. Ж:

673. Ж:

674. Ж:

675. Ж:

676. Ж:

677. Ж:

Келесі функцияларды -ң дәрежесі бойынша қатарға жіктеу керек.

678. Ж:

679. Ж:

680. Ж: .

681. Ж:

682. функциясын нүктесінде дәрежесі төртінші ретті мүшесіне дейін жіктеу керек.

Ж:

683. функциясын нүктесінде дәрежесі төртінші ретті мүшесіне дейін жіктеу керек. Ж:

684. функциясын нүктесінде дәрежесі төртінші ретті мүшесіне дейін жіктеу керек. Ж:

685. функциясын нүктесінде дәрежесі үшінші ретті мүшесіне дейін жіктеу керек. Ж:

Келесі сандарды 0,0001 дәлдікпен есептеу керек.

686. Ж: 0,9511. 687. Ж: 1,6487.

688. Ж: 0,1973. 689. Ж: 0,6931.

690. Ж: 1,6094. 691. Ж: 1,6487.

692. Ж: 3,0801. 693. Ж: 5,0666.

694. Ж: 0,6065. 695. Ж: 0,0392.

696. х-тің қандай мәндерінде формуласы 0,01; ,001; 0,0001 сандарынан артық болмайтын қателіктер жібереді?

Ж: .

697. х-тің қандай мәндерінде формуласы 0,01; 0,001; 0,0001 сандарынан артық болмайтын қателіктер жібереді?

Ж: .

Төмендегі шектерді Тейлор қатарының көмегімен есептеу керек.

698. Ж: . 699. Ж: 1.

700. Ж: . 701. Ж: .

Тейлор қатарының көмегімен төмендегі анықталған интегралдарды дәлдіктермен есептеу керек.

702. Ж: 0,7468.

703. Ж: 0,4931.

704. Ж: 0,487.

705. Ж: 0,2483.

706. Ж: 0,071.

707. Ж: 0,2505.

708. Ж: 0,102.

709. Ж: 0,2483.