8. 2 Сурет
▲
934.
933-есепте қарастырылған Х кездейсоқ
шаманың мәндері
интервалына түсу ықтималдығын табу
керек.
Шешуі.
.
▲
935. 932-есепте берілген үлестірім функциясының үлестірім тығыздығын табу керек.
Шешуі.
▲
936. Үзіліссіз кездейсоқ шама Х-ң үлестірім тығыздығы
берілген.
Тұрақты
санын табу керек.
Шешуі.
Үлестірім тығыздығының қасиеті бойынша
осыдан
немесе
.
Сонымен
. ▲
937. Үзіліссіз кездейсоқ шама Х-њ үзіліссіз ‰лестірім тығыздығы
берілген.
Оның
интервалына түсу ықтималдығын табу
керек.
Шешуі.
. ▲
938.
Үзіліссіз Х кездейсоқ шаманың үзіліссіз
үлестірім тығыздығы
Берілген кездейсоқ шаманың:
а) үлестірім функциясын табу керек,
ә) үлестірім тығыздығы мен функцияның графигін салу керек.
Шешуі.
а)
формуласын қолданамыз.
Егер
болса, онда
.
Осыдан
болады.
Егер
болса, онда
.
Олай болса
.
Егер
болса, онда
.
Сонымен
.
ә) Үлестірім тығыздығы мен функцияның графигін салайық (8.3,8.4 Суреттер)
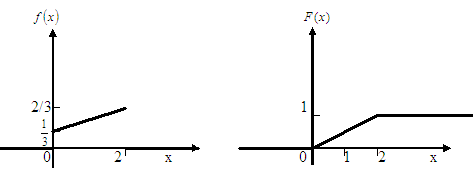
8.3 Сурет 8.4 Сурет
2. Үзіліссіз кездейсоқ шаманың сандық сипаттамалары. Үзіліссіз кездейсоқ шама Х-ң математикалық үміті
формуласын
анықталады. Егер барлық мүмкін мәндері
интервалына тиісті болса, онда
.
Үзіліссіз
Х кездейсоқ шаманың
модасы деп
оның үлестірім тығыздығының максимуміне
сәйкес келетін кездейсоқ шаманың мәнін
айтады.
Үзіліссіз
Х кездейсоқ шаманың
медианасы
деп
теңдігімен анықталатын кездейсоқ
шаманың мәнін айтады.
Үзіліссіз Х кездейсоқ шаманың дисперсиясы
немесе
формуласымен
анықталады. Егер барлық мүмкін мәндері
интервалына тиісті болса, онда
немесе
.
Жоғарыда көрсетілген дискретті кездейсоқ шаманың математикалық үмітімен дисперсиясының барлық қасиеттері үзіліссіз Х кездейсоқ шамасының математикалық үмітімен дисперсиясы үшін де орындалады.
Үзіліссіз
Х кездейсоқ шаманың орташа
квадраттық ауытқуы
формуласымен анықталады.
Үзіліссіз Х кездейсоқ шаманың -ретті бастапқы моменті
,
-ретті
орталық моменті
асимметриясы
және эксцессі
формулаларымен анықталады. Дербес
жағдайларда
,
,
,
,
.
Егер
үзіліссіз Х кездейсоқ шамасы
аралығында анықталып, оның үлестірім
тығыздығы
формуласымен берілсе, онда кездейсоқ шама бірқалыпты үлестірім заңымен берілді делінеді.
Егер үзіліссіз Х кездейсоқ шамасының үлестірім тығыздығы
формуласымен берілсе, онда кездейсоқ шаманы көрсеткішті үлестірім заңымен берілді дейді.
Үзіліссіз Х кездейсоқ шамасының үлестірім тыѓыздыѓы
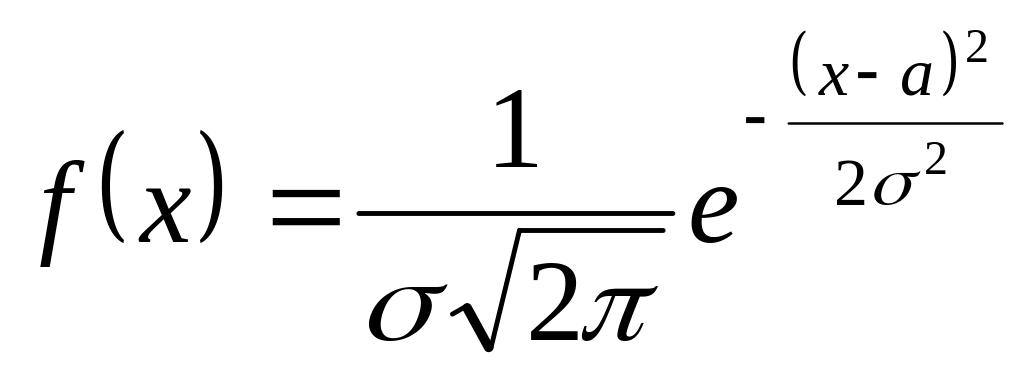
формуласымен
берілсе, онда кездейсоқ шаманы қалыпты
үлестірім заңымен берілді дейді,
мұндағы
- математикалық үміт, ал
- орташа квадраттық ауытқу болады.
Үлестірім
функциясы
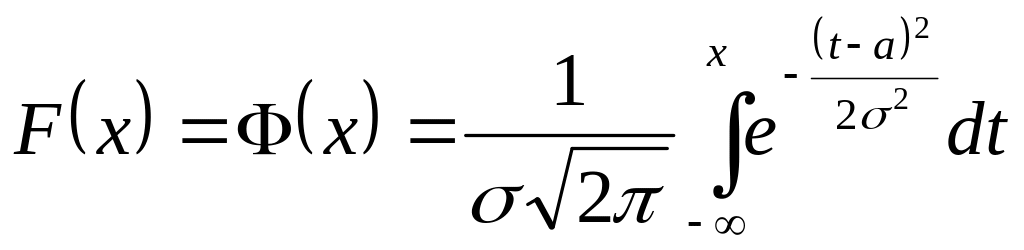формуласымен анықталады, оның мәндері
1-кестеде берілген. Х кездейсоқ шамасының
мәндері
интервалында болу ықтималдығы
формуласымен анықталады.
Х
кездейсоқ шамасының математикалық
үмітінен ауытқуының абсолют мәні оң
санынан кіші болу ықтималдығы
формуласымен анықталады. Бұл жағдайда
.
939. Үзіліссіз Х кездейсоқ шаманың үлестірім функциясы
,
,
табу
керек.
Шешуі. Алдымен үлестірім тығыздығын табу керек.
Енді,
,
,
.
Үлестірім
тығыздық
интервалында сызықты функция, сондыќтан
осы аралықта оның максимумы жоқ, олай
болса кездейсоқ шаманың модасы жоқ.
немесе
формуласымен табылады, олай болса
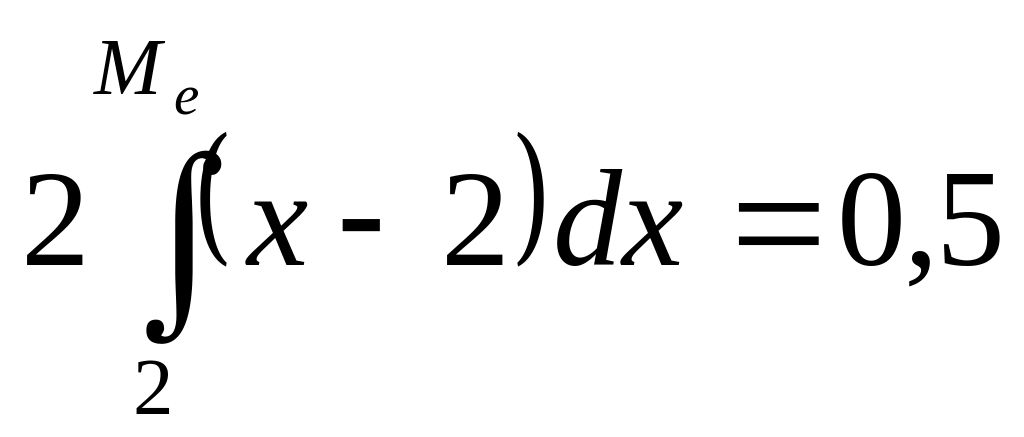немесе
теңдеуінен
осыдан
болғандықтан
. ▲
940. Үзіліссіз Х кездейсоқ шаманың үлестірім тығыздығы
берілген. Кездейсоқ шаманың модасын табу керек.
Шешуі.
,
осыдан
,
.
Олай
болса функция
нүктесінде максимум мәніне тең болады.
Осыдан
. ▲
941. Бір қалыпты үлестірім заңымен берілген Х кездейсоқ шамасының үлестірім функциясын, математикалық үмітін, дисперсиясын және орташа квадраттық ауытқуын табу керек.
Шешуі. формуласын қолданайық.
Егер болса, онда .
Егер
болса, онда
.
Егер
болса, онда
.
Осыдан
.
.
. ▲
942.
Көрсеткішті үлестірім заңымен берілген
Х кездейсоқ шамасының үлестірім
функциясын, математикалық үмітін,
дисперсиясын, орташа квадраттық ауытқуын,
кездейсоқ шаманың мүмкін мәндерінің
интервалында болу ықтималдығын табу
керек.
Шешуі. Алдымен функциясын табайық.
Егер
болса, онда
.
Егер
болса, онда
.
Осыдан
.
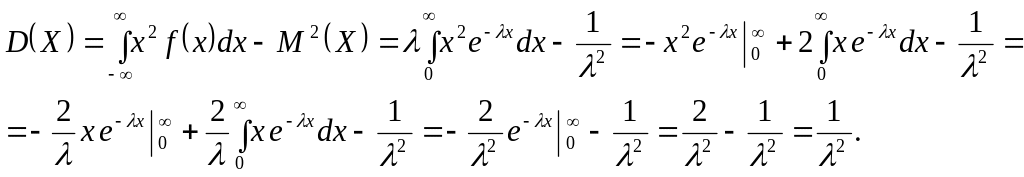
Осыдан
;
. ▲
943.
Кездейсоқ шама қалыпты үлестірім заңымен
берілген. Математикалық үміті
,
дисперсиясы
.
Кездейсоқ шаманың мәндері (50,80)
интервалында болу ықтималдығын табу
керек.
Шешуі.
▲
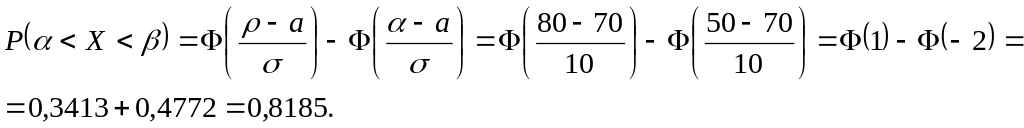
944. Үзіліссіз Х кездейсоқ шаманың үлестірім функциясы
Кездейсоқ шаманың мәндерінің
а)
(3; 4), є) (3; 6), б) (1; 4), в) (1; 7) интервалына
түсу ықтималдығын табу керек. Ж:
a)
ә)
б)
в) 1.
945. Х кездейсоқ шамасының үлестірім функциясы
