Қатарлар
Сан қатары
1.
Мүшелері оң сан қатарлары.
қандай да бір сан тізбегі берілсе, онда
(7.1)
шексіз қосындыны сан қатары деп атайды.
Мұндағы
сандары сан қатарларының мүшелері,
ал
саны жалпы мүшесі
(немесе n-ші мүшесі) деп
аталады.
Жалпы
мүшесі арқылы сан қатарын қысқаша
деп жазуға болады.
(7.1)-қатардың алғашқы мүшелерінің қосындыларын қарастырайық.
қатардың
дербес қосындылары
деп аталады.
Егер сан қатарының алғашқы мүшелерінің қосындылар тізбегінің шегі бар болса, яғни
(7.2)
саны бар болса, онда ол қатардың қосындысы деп аталады, және қатар жинақты делінеді.
Егер (7.2) шегі болмаса, онда берілген сан қатарын жинақсыз дейміз, ондай қатардың қосындысы жоқ.
Сан қатарының негізгі теоремаларын қарастырайық:
а) егер қатары жинақты болса, онда алғашқы m мүшелерін алып тастағанда пайда болған
(7.3)
қатары да жинақты болады. Керісінше алғашқы m мүшелері алынып тасталынған қатар жинақты болса, онда берілген қатарда жинақты болады.
(7.3)-қатарды берілген қатардың m-ші қалдығы деп атайды;
ә)
егер
қатары
жинақты және қосындысы S-ке тең болса,
онда
қатары да жинақты және қосындысы
-ке
тең болады;
б)
егер
және
қатарлары жинақты және қосындылары
сәйкесінше
және
болса, онда
қатары да жинақты және қосындысы
-ға
тең болады.
Көп жағдайларда қатардың алғашқы n мүшелерінің қосындысы арқылы оның жинақты немесе жинақсыз болуын тексеру өте қиын немесе күрделі есептеуді қажет етеді. Сондықтан қатардың жинақтың немесе жинақсыз болуын білу үшін жинақтылық белгілерінқарастырамыз.
Қ а т а р ж и н а қ т ы л ы ғ ы н ы ң қ а ж е т т і б е л г і с і.
Егер
қатар жинақты болса, онда
-да
оның жалпы (n-ші) мүшесі нөлге ұмтылады,
яғни
Ал
егер
болса, онда қатар жинақсыз болады.
Қ а т а р ж и н а қ т ы л ы ғ ы н ы ң ж е т к і л і к т і б е л г і л е р і
а)
І с а л ы с т ы р у б е л г і с і.
(7.4)
және
(7.5)
қатарлары
берілсін және
болсын.
Егер (7.5)-қатар жинақты болса, онда (7.4)-қатар да жинақты болады.
Егер (7.4)-қатар жинақсыз болса, онда (7.5)-қатар да жинақсыз болады.
ә)
ІІ с а л ы с т ы р у б е л г і с і. Егер
ақырлы шегі бар болса, онда
және
қатарлары екеуі де бірдей жинақты немесе
бірдей жинақсыз болады.
б)
Д а л а м б е р б е л г і с і. Мүшелері
оң болатын
қатары үшін
болса, онда:
1)
болғанда, қатар жинақсыз;
2)
болғанда, қатар жинақты;
3)
болғанда, қатар жинақты да немесе
жинақсыз да болуы мүмкін.
в) К о ш и б е л г і с і. Мүшелері оң болатын қатары үшін
болса, онда:
1)
болғанда, қатар жинақсыз;
2)
болғанда, қатар жинақты;
3)
болғанда, қатар жинақты да немесе
жинақсыз да болуы мүмкін.
г)
К о ш и д і ң и н т е г р а л д ы қ б е л
г і с і. Мүшелері оң және өспейтін
қатары берілсін (яғни
және
болсын. Мұндағы
- өспейтін үзіліссіз функция.
Егер
меншіксіз интегралы жинақты болса, онда
қатары да жинақты болады.
Егер меншіксіз интегралы жинақсыз болса, онда қатары да жинақсыз болады.
492.
қатарының жалпы мүшесі берілген. Алғашқы
мүшелерін табу керек.
Шешуі.
▲
493.
қатарының
жалпы мүшесі берілген. Алғашқы бес
мүшелерін табу керек.
Шешуі.
▲
494.
қатарының жалпы мүшесін табу керек.
Шешуі.
Алымында 1, 3, 5, ... сандарынан тұратын
тізбек арифметикалық прогрессия құрайды,
оның n-ші мүшесін
формуласы бойынша табамыз. Мұнда
сондықтан
Бөліміндегі
сандары геометриялық прогрессия құрайды,
оның n-ші мүшесі
-ге
тең. Осыдан жалпы мүшесі
▲
495.
қатарының жалпы мүшесін табу керек.
Шешуі.
Әрбір мүшесінің дәрежесі мүшесінің
нөмірімен сәйкес келеді. Сондықтан n-ші
мүшесінің дәрежесі n-ге тең болады.
бөлшектерінің алымы бірінші мүшесі
3-ке, айырмасы 1-ге тең арифметикалық
прогрессияны құрайды. Онда n-ші мүшесі
-ке
тең болады, ал бөлімі бірінші мүшесі
5-ке, айырмасы 3-ке тең арифметикалық
прогрессияны құрайды, осыдан n-ші мүшесі
-ке
тең болады. Сонымен қатардың жалпы
мүшесі
▲
496.
қатарының жалпы мүшесін табу керек.
Шешуі.
болады. ▲
497.
Мүшелері геометриялық прогрессия
болатын
сан қатарының жинақтылығын зерттеу
керек.
Шешуі.
Мектеп бағдарламасынан белгілі:
Егер
болса, онда қосынды
Олай болса, қатар жинақты.
Ал
егер
болса, онда берілген қатар жинақсыз,
себебі:
сондықтан
Егер
болса, онда қатардың алғашқы n мүшелерінің
қосындысы
Осыдан
яғни қатар жинақсыз.
Егер
болса, онда қатарды
түрінде жазуға болады. Яғни оның алғашқы
n мүшесінің қосындысы
Бұл жағдайда қатардың қосындысы анықталмаған, яғни қатар жинақсыз.
Сонымен мынадай қорытынды жасауға болады:
Егер
болса, онда қатар жинақты, ал егер
болса, онда қатар жинақсыз болады. ▲
498.
сан қатарының жинақтылығын зерттеу
керек.
Шешуі.
Қатардың жалпы мүшесін
екі бөлшектің жарты айырымы ретінде
көрсетуге болады.
,
яғни
олай болса,
деп
жазуға болады. Осыдан
яғни қатар жинақты. ▲
499.
қатарының жинақтылығын зерттеу керек.
Шешуі. Берілген қатар шексіз кемімелі геометриялық прогрессияның мүшелерінен құралған. Олай болса, қатар жинақты. Оның қосындысын табайық, мұнда
▲
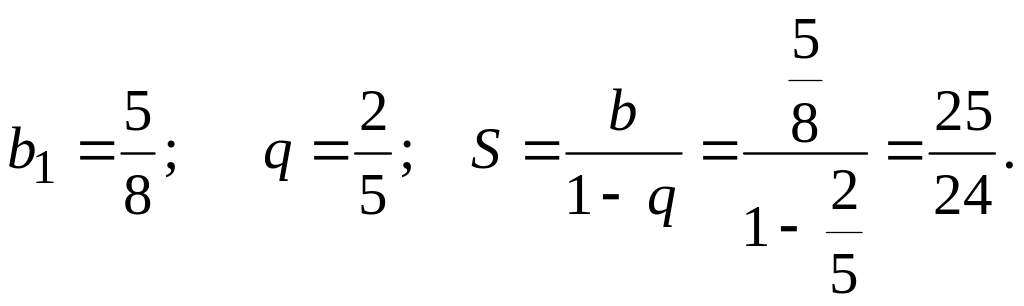500.
қатарының жинақтылығын зерттеу керек.
Шешуі.
Қатардың жалпы мүшесін
түрінде жазсақ, онда қатарды әрқайсысы
геометриялық прогрессияның мүшелерінен
құралған
екі қатардың қосындысы түрінде жазуға
болады. Бұл екі қатар да жинақты болады
және олардың қосындысы
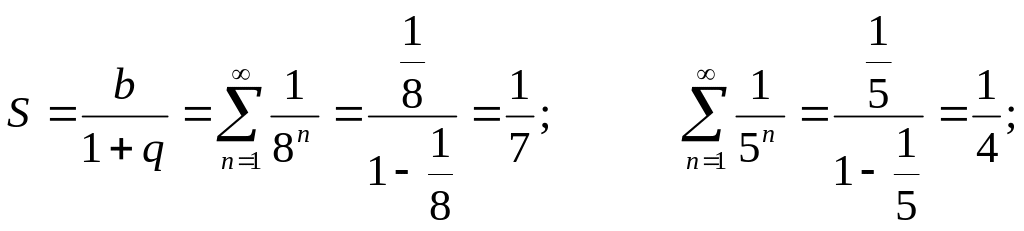
олай
болса,
▲
501.
қатарының жинақтылығын зерттеу керек.
Шешуі.
Осыдан қатардың жинақтылығының қажетті белгісі орындалмағандықтан, қатар жинақсыз болады. ▲
502.
қатарының жинақтылығын зерттеу керек.
Шешуі.
онда қатар жинақсыз болады. ▲
503.
қатарының жинақтылығын зерттеу керек.
Шешуі.
яғни қажетті белгісі орындалады. Енді
-шексіз кемімелі геометриялық прогрессияның
мүшелерінен құралған қатарды қарастырайық.
Бұл қатар жинақты болады.
теңсіздіктері орындалғандықтан, берілген
қатар да жинақты болады; ▲
504.
Жалпы мүшесі
тең болатын қатардың жинақтылығын
зерттеу керек.
Шешуі.
Берілген қатарды жалпы мүшесі
болатын жинақты қатармен салыстырайық.
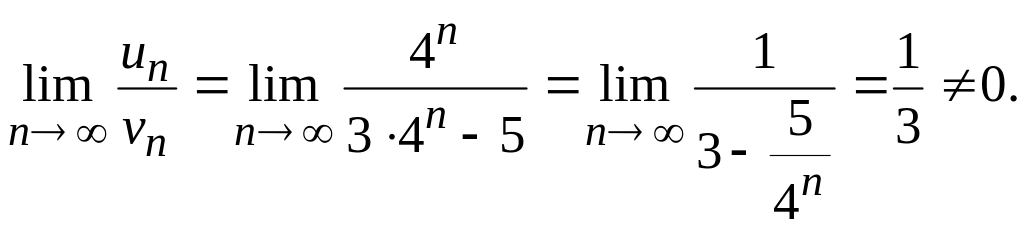
Яғни ІІ салыстыру белгісі бойынша берілген қатар жинақты болады; ▲
505.
қатарының жинақтылығын зерттеу керек.
Шешуі.
Даламбер белгісі
бойынша:
яғни
қатар жинақты.
▲
506.
қатарының жинақтылығын зерттеу керек.
Шешуі.
яғни
қатар жинақты болады (Даламбер белгісі
бойынша). ▲
507.
қатарының жинақтылығын зерттеу керек.
Шешуі.
қатар
жинақты (Даламбер белгісі бойынша). ▲
508.
қатарының жинақтылығын зерттеу керек.
Шешуі.
қатар жинақты (Коши белгісі бойынша).
▲
509.
қатарының жинақтылығын зерттеу керек.
Шешуі.
мұндағы
яғни қатар жинақты (Коши белгісі
бойынша). ▲
510.
қатарының жинақтылығын зерттеу керек.
Шешуі.
яғни қатар жинақты (Коши белгісі
бойынша). ▲
511.
Дирихле қатарының жинақтылығын зерттеу
керек.
Шешуі.
олай болса,
болғанда қатардың жинақтылығының
қажетті белгісі орындалады.
Енді жеткілікті белгісін қарастырайық. Даламбер белгісін қолданайық:
осыдан Даламбер белгісінің көмегімен қатардың жинақтылығын зерттеу мүмкін еместігін көруге болады. Сол сияқты Коши белгісінің көмегімен тексерсек:
болады,
яғни бұл жағдайда да қатардың жинақтылығы
туралы ешнәрсе айтуға болмайды. Енді
Кошидің интегралдық белгісін қолданайық.
Ол үшін
функциясын қарастырамыз. Себебі
Осыдан,
егер
болса, онда
ал егер
болса, онда
Сонымен мынадай қорытындыға келуге
болады, егер
болса, онда
қатары жинақты, ал егер
болса, онда ол жинақсыз болады.
болғанда
, яғни
жинақсыз қатары гармоникалық
қатар деп аталады. ▲
512.
қатарының жинақтылығын зерттеу керек.
Шешуі.
Қатардың жинақтылығының қажетті белгісі
орындалғанымен, берілген қатар жинақсыз
болады. Себебі
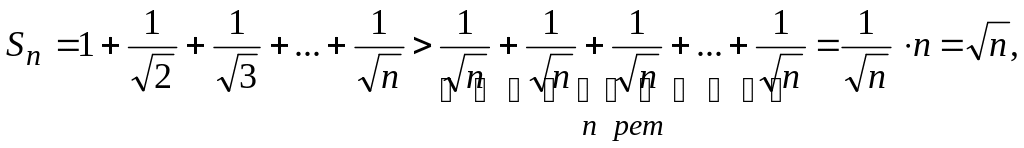яғни
Осыдан
қатардың жинақтылығының қажетті белгісі
орындалғанымен, оның жинақтылығы немесе
жинақсыздығы белгісіз болатындығын
байқаймыз. Сондықтан қатардың жинақтылығын
зерттеу үшін жеткілікті белгісін
қарастыруымыз керек. Дәреже
болғандықтан (511 –мысалды қараңыз)
қатар жинақсыз. ▲
513.
қатарының жинақтылығын зерттеу керек.
Шешуі.
Қатардың жалпы мүшесінің алымының
дәрежесі төртке, ал бөлімінің дәрежесі
беске тең. Алымы мен бөлімінің дәрежелерінің
айырмасы бірге тең. Сондықтан, берілген
қатарға екінші салыстыру белгісін
қолданып,
гармоникалық қатарымен салыстырамыз.
болғандықтан,
берілген қатар да жинақсыз болады. ▲
514.
қатарының жинақтылығын зерттеу керек.
Шешуі. Қатардың жалпы мүшесінің алымының дәрежесі бірге, бөлімінің дәрежесі үшке тең, олай болса айырмасы екіге тең болады. Сондықтан
жинақты қатарымен салыстыра отырып, берілген қатардың жинақты екендігін көреміз. ▲
515.
қатарының жинақтылығын зерттеу керек.
Шешуі.
әрі
орындалатындықтан
функциясын аламыз.
,
осыдан қатар жинақсыз (Кошидің интегралдық
белгісі бойынша). ▲
2. Ауыспалы таңбалы қатар. Лейбниц белгісі. Қатар тұрған мүшелерінің таңбалары әртүрлі болатын қатарларды ауыспалы таңбалы қатар дейміз.
Ондай қатарларды
деп
жазамыз, мұндағы
.
Осындай ауыспалы таңбалы қатарлардың
жинақтылығы Лейбниц белгісі арқылы
анықталады:
Л е й б н и ц б е л г і с і. Егер ауыспалы таңбалы
,
яғни қатар мүшелерінің абсолюттік
мәндері кемімелі және
болса,
онда
қатар жинақты (әрі оның қосындысы бірінші
мүшесінен кем болады, яғни
).
Қатардың
қосындысын
түрінде жазуға болады. Мұндағы
қатардың
n-ші қалдығы
деп аталады.
Осы
қалдықтың да таңбалары ауыспалы қатар
болғандықтан, Лейбниц белгісін қолдануға
болады, олай болса
Осыдан жуықтап есептеу кезінде
ал
-
жіберілген қатесі болып табылады.
Таңбалары айнымалы
қатары және осы қатардың мүшелерінің абсолют мәні бойынша алынған
қатары берілсін.
Егер
-қатары жинақты болса, онда
-қатары да жинақты болады. Бұл жағдайда
- қатары абсолютті
жинақты дейді.
Егер -қатары жинақты, ал -қатары жинақсыз болса, онда -қатары шартты жинақты деп аталады.
516.
қатарын
дәлдікпен есептеу керек.
Шешуі.
осы қатардың бірнеше мүшелерін есептейік:
Осыдан
▲
517.
қатарының жинақтылығын зерттеу керек,
мұнда
кез келген сан.
Шешуі. Берілген қатардың мүшелерінің абсолют мәні арқылы алынған қатарды қарастырамыз:
қатары
жинақты, себебі І салыстыру белгісі
бойынша
ал
қатары жинақты (511-мысалды қараңыз,
).
Осыдан берілген қатар абсолют жинақты. ▲
518.
қатарының абсолют немесе шартты
жинақтылығын зерттеу керек.
Шешуі.
Мүшелерінің абсолютті мәні бойынша
құрылған
қатарын қарастырайық. Бұл қатар жинақты,
себебі екінші салыстыру белгісі бойынша
21-мысалда көрсетілгендей
қатарымен салыстырайық, онда
Олай болса, берілген қатар абсолют жинақты болып табылады. ▲
519.
қатарының абсолютті немесе шартты
жинақтығын зерттеу керек.
Шешуі. Лейбниц белгісін қолданайық:
,
әрі
. Олай болса, қатар жинақты.
Енді
мүшелерінің абсолют мәні арқылы алынған
қатарын қарастырайық. Бұл қатар
гармоникалық қатар, ал ол жинақсыз
болғандықтан берілген қатар шартты
жинақты болады. ▲
Қатардың алғашқы бес мүшесін жазу керек.
520.
Ж:
.
521.
Ж:
.
522.
Ж:
.
523.
Ж:
.
524.
Ж:
.
525.
Ж:
.
526.
Ж:
.
527.
Ж:
.
Қатардың жалпы мүшесін жазу керек.
528.
Ж:
. 529.
Ж:
.
530.
Ж:
.531.
Ж:
.
532.
Ж:
. 533.
Ж:
.
534.
Ж:
. 535.
Ж:
.
Қатарлардың жинақтылығын зерттеу керек.
536.
Ж:
Жинақты. 537.
Ж:
Жинақты.
538.
Ж:
Жинақсыз. 539.
Ж:
Жинақсыз.
540.
Ж:
Жинақты. 541.
Ж:
Жинақты.
542.
Ж:
Жинақты. 543.
Ж:
Жинақты.
544.
Ж:
Жинақты. 545.
Ж:
Жинақты.
546.
Ж:
Жинақты. 547.
Ж:
Жинақты.
548.
Ж:
Жинақсыз.
549.
Ж:
Жинақсыз.
550.
Ж:
Жинақсыз.
551.
Ж:
Жинақсыз.
552.
Ж:
Жинақты. 553.
Ж:
Жинақты.
554.
Ж:
Жинақты. 555.
Ж:
Жинақты.
556.
Ж:
Жинақты. 557.
Ж:
Жинақты.
558.
Ж:
Жинақты.
559.
Ж:
Жинақты.
560.
Ж:
Жинақты.
561.
Ж:
Жинақты.
562.
Ж:
Жинақты.
563.
Ж:
Жинақты.
564.
Ж:
Жинақты.
565.
Ж:
Жинақты.
566.
Ж:
Жинақсыз.
567.
Ж:
Жинақты.
568.
Ж:
Жинақты.
569.
Ж:
Жинақты.
570.
Ж:
Жинақты.
571.
Ж:
Жинақты.
572.
Ж:
Жинақсыз. 573.
Ж:
Жинақты.
574.
Ж:
Жинақсыз. 575.
Ж:
Жинақты.
576.
Ж:
Жинақты. 577.
Ж:
Жинақты.
578.
Ж:
Жинақты. 579.
Ж:
Жинақсыз.
580.
Ж:
Жинақты. 581.
Ж:
Жинақсыз.
582.
Ж:
Жинақты. 583.
Ж:
Жинақты.
584.
Ж:
Жинақсыз. 585.
Ж:
Жинақты.
586.
Ж:
Жинақты. 587.
қатары берілген.
Ж: Ескерту. Кошидің интегралдық белгісін пайдаланған жөн.
Ауыспалы таңбалы қатардың жинақтылығын зерттеу керек. Жинақты болған жағдайда, оның абсолютті немесе шартты жинақты болатындығын зерттеу керек.
588.
Ж:
Шартты жинақты.
589.
Ж:
Жинақсыз.
590.
Ж:
Шартты жинақты.
591.
Ж:
Абсолют жинақты.
592.
Ж:
Абсолют жинақты.
593.
Ж:
Шартты жинақты.
594.
Ж:
Жинақсыз.
595.
Ж:
Шартты жинақты.
596.
Ж:
Абсолют жинақты.
597.
Ж:
Шартты жинақты.
598.
Ж:
Абсолют жинақты.
599.
Ж:
Абсолют жинақты.
Қатарларды дәлдікпен есептеу керек.
600.
Ж:
0,632. 601.
Ж:
0,841.
602.
Ж:
0,459. 603.
Ж:
0,645.