4. Модель Ли «от точки к точке»

Эта модель «от точки к точке» позволяет предска­зать уровень сигнала с учетом профиля трассы (рельефа и пара­метров застройки). При этом предлагается разделять трассы по профилю рельефа местности на открытые и закрытые, подобно тому как это делают для трасс РРЛ. Только в отличие от РРЛ, на мобильной радиолинии на открытой трассе, как правило, нет прямой видимости между антеннами БС и МС, поскольку линию прямой видимости перекрывают городские строения.

В общем виде вместо (1.15) можно записать

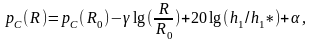(1.21)

где - уровень мощности сигнала на расстоянии от БС при типовых энергетических параметрах аппаратуры указанных в табл.6.; - результирующий поправочный коэффициент. В (1.21) фактор «высота – усиление антенны БС», позволяет рассчитать изменение коэффициента усиления антенны БС при изменении профиля трассы

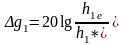, (1.22)

где - эффективная высота антенны БС для конкретного уча­стка трассы.

Напомним, что в моделях «от зоны к зоне» эффективная высота антенны БС определяется как высота над средним уровнем квазигладкой поверхности. Для модели «от точки к точке» эффективная высота антенны БС зависит от рельефа трасы и может изменяться при движении МС.

Открытые трассы. Для определения эффективной высоты антенны на профиле трассы выполняют следующие по­строения (рис. 11). Определяют потенциальную точку z отраже­ния радиоволн от земной поверхности, для чего соединяют антенну БС с зеркальным изображением антенны МС. Точка пересечения этой линии с земной поверхностью и есть z.

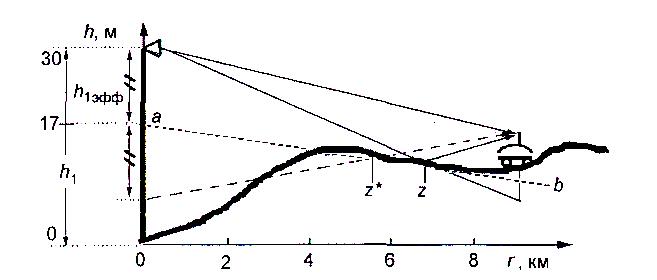
Рис. 11. К определению эффективной высоты антенны БС

Строят плоскость от­ражения от Земли, как касательную к профилю трассы в точке z. Продолжают ее до пересечения с высотой антенны БС. След этой плоскости - линия . Из рис.11. находим эффективную высоту антенны БС - .

Для данного примера по (1.22)

дБ.

Эффективная высота антенны меньше ре­альной, и соответственно уменьшился уровень сигнала в точке приема.

Так же можно определить вторую потенциальную точку отраже­ния на этой плоскости z*, соединив антенну МС с зеркальным изо­бражением антенны БС ( ). Из двух потен­циальных точек отражения рекомендуется рассматривать ту, кото­рая ближе к МС, поскольку значительная часть отраженной от нее энергии может попасть к МС. При нахождении точки z следует пом­нить, что при построении профиля трассы используют разные гори­зонтальный (Г) и вертикальный (В) масштабы. Например, если для высот в 1 см-100м (1:10 000), а для расстояний - 1:100 000 – 1 км в 1 см, то коэффи­циент отношения масштабов Г/В составляет . Углы падения и отражения на чертеже профиля в системе координат с различ­ными масштабами равны только в случае, когда плоскость отраже­ния горизонтальна. В других случаях нет. Приведенный выше метод определения точки отражения применим при . При применяют более точные методы.

На рис.12. эффективная высота антенны увеличилась. В этом случае

дБ.

Рис.12. К определению эффективной высоты антенны для МС на холме

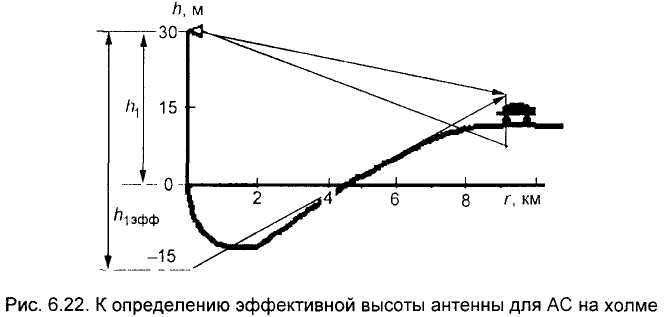
Эффективная высота антенны БС будет меняться при движении МС, хотя реальная высота остается постоянной. Соответственно будет меняться уровень сигнала в точке приема.

Необходимость учитывать эффективную высоту антенны в

Рис.12. К определению эффективной высоты антенны для МС на холме.

место реальной иллюстрирует рис. 13. На рис.13,а высота Н >> h₂ и длина подстилающей поверхности соизмерима с длиной автомо­биля. В этом случае на приемник МС приходит только одна прямая волна 1 и условия распространения такие же, как в свободном про­странстве. Ситуация на рис.13,б отличается только тем, что зна­чительно увеличилась длина , так что может быть указана потен­циальная точка отражения от подстилающей поверхности. На при­емник МС приходят два сигнала: прямой 1 и отраженный 2. По­скольку расстояние R обычно составляет несколько километров, а высоты антенн порядка 3...30 м, то угол скольжения очень мал. При этом фаза коэффициента отражения около 180°. В случае, ко­гда имеет место зеркальное отражение, могут возникать глубокие замирания сигнала на приеме.

R

R

а) б)

Рис.13. К учету эффективной высоты антенны при малых (а) и больших (б) размерах подстилающей поверхности

На местности с большим уклоном сигнал, приходящий на МС, будет слабым, поскольку рельеф местности ослабляет пря­мую волну. Эффективная высота антенны становится очень малой.

Отражения от водной поверхности носит зеркальный характер. Для систем с фиксированными станциями, например РРЛ, при расчете трасс над водной поверхностью используется двухлучевая модель (рис.14,а), а при расчете подобных трасс для систем подвижной связи - трехлучевая модель Ли (рис.14,б). При этом предполагается, что волны 2 и 3 складываются в противофазе и компенсируют друг друга. Уровень сигнала такой же как в свобод­ном пространстве.

Рис.14. Модели для учета влияния водной поверхности: двухлучевая (а) и трехлучевая (б)

Влияние городской инфраструктуры. На уровень сигнала влияет плотность застройки. При плотной застройке уровень сигна­ла на приеме ниже, чем при редкой.

При плотной застройке различают варианты:

• Прямая видимость между антеннами БС и МС. Уровень радиоволн, отраженных зданиями мал, в сравнении с ос­новным сигналом. Замирания сигнала подчиняются закону Райса.

• Линия прямой видимости перекрыта строениями. Замирания сигнала подчиняются закону Релея.

В этих двух случаях средняя мощность принимаемого сигнала не одинакова. Однако различия малы, если мощность отраженных волн значительна. В обоих случаях потери распространения со­ставляют примерно 40 дБ на декаду.

Закрытые трассы. На них линия прямой видимости перекрыта профилем местности из-за чего имеют место дифракционные потери. Их рассчитывают, применяя теорию дифракции радиоволн на препятствии клиновидной формы. Выполняют построения, показанные на рис.15.

Рис.15. К пояснению определения параметров препятствия

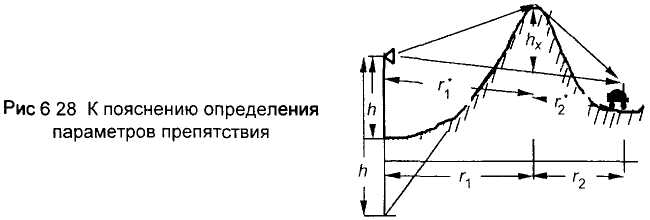
По профилю трассы определяют три параметра: - расстояние от БС до вершины холма; - расстояние от вершины холма до МС; - высоту холма с клиновидной вершиной. И вычисляют параметр :

(1.23)

где - длина волны.

Высота препятствия в расчете может принимать отрицательное значение ( ). Это означает, что трасса открытая и нет ди­фракционных потерь.

Дифракционные потери выражаются в деци­белах. Известно аналитическое представление величины че­рез интегралы Френеля. В инженерной практике пользуются гра­фическим представлением , а также выраже­ниями, аппроксимирующими эти графики.

Ha касательной трассе если то = 6 дБ.

Двойная дифракция. Это случай, когда на трассе имеется не­сколько холмов. Здесь может возникнуть двойная или даже более сложная дифракция. Для расчета значения потерь используются модели Буллингтона, Эпштейна и Питерсона и др. При использовании модели Пиквинарда определяют высоты холмов, например, С - и D - . Находят дифракционные потери отдельно для каждого холма: и . Общие потери .

Выводы.

Для модели Ли «от точки к точке» в качестве основной принята формула (1.21), которая может быть распространена на следующие случаи:

1. Открытая трасса. Используют формулу

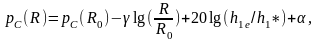. (1.24)

2. Закрытая трасса.

(1.252)

где - условная эффективная высота антенны БС на закрытой трассе.

3. Пролет БС - МС над водной поверхностью. Справедлива формула для свободного пространства.

Условную эффективную высоту антенны БС на закрытой трассе часто определить нельзя (не существует). В таком случае принимают = .