5. Высотное обоснование топографических и кадастровых съемок.

Сгущение государственных нивелирных сетей I , II, III и IV классов осуществляют для развития высотных сетей сгущения и съемочных сетей. Высотные сети сгущения и съемочные сети, как правило, создают методами

геометрического или тригонометрического нивелирования. Для обеспечения топографических съемок с высотой сечения горизонталей до 1 м и для инженерных изысканий в качестве высотного обоснования используют ходы геометрического нивелирования, а для топографических съемок и изысканий на ранних стадиях проектирования допускается использовать ходы тригонометрического нивелирования.

Обычно пункты плановых сетей сгущения и съемочных сетей используют одновременно и в качестве пунктов высотного обоснования. Высотную привязку к реперам и маркам государственной нивелирной сети теодолитных ходов замкнутых (полигонов) и разомкнутых (трасс) обычно осуществляют двойным нивелированием в прямом и обратном

направлениях. При этом замкнутые полигоны, как правило, привязывают к одному пункту государственной нивелирной сети. Длинные теодолитные ходы (трассы) обычно привязывают к реперам и маркам в начале и конце, а при очень длинных трассах осуществляют периодическую привязку и промежуточных точек.

Допустимую невязку двойного хода при привязке к реперам и маркам принимают ± 50 , мм (где L—длина двойного нивелирного хода, км).

При нивелировании теодолитных ходов всегда возникает задача контроля и уравновешивания нивелирного хода.

Уравновешивание замкнутого нивелирного хода

Теоретическая сумма превышений в замкнутом нивелирном ходу, очевидно, должна равняться нулю .

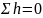Однако в связи с неизбежной погрешностью измерений сумма превышений оказывается отличной от нуля

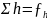(14.21)

Если величина невязки в превышениях , оказывается меньше предельно допустимой, то выполняют уравнивание нивелирного хода, т. е. распределяют невязку с обратным знаком между соответствующими превышениями пропорционально длинам сторон: (14.22)

Для уравненного замкнутого нивелирного хода должно быть получено: = 0. (14.23)

Для разомкнутых теодолитных ходов (трасс), привязанных в начале и конце к пунктам государственной нивелирной сети, высоты которых определены нивелированием соответствующих более высоких классов, можно записать

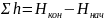, где 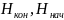— соответственно, высоты реперов государственной нивелирной сети в конце и начале трассы.

В связи с наличием неизбежной погрешности измерений фактически нужно написать:

Если невязка в превышенияхоказывается меньше допустимой, осуществляют уравнивание разомкнутого нивелирного хода, так же как и для замкнутого введением поправок (14.22) к соответствующим величинам превышений, при этом для уравненного разомкнутого нивелирного хода должно быть получено:

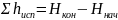
Для высотного обоснования топографических съемок и инженерных изысканий весьма эффективным оказывается использование приемников спутниковой навигации «GPS» геодезического класса точности.

6. Критерии, используемые при оценке точности измерений. Правила геодезических вычислений. (Не уверена на счет этого вопроса. Именно такой формулировки нигде не нашла. Нашла только про критерий оценки точности. Не знаю то это или нет.)

Измерением называют процесс сравнения измеряемой величины с другой, принятой за единицу измерения известной величиной. Измерения различают: прямые, косвенные и дистанционные.

Прямые измерения являются простейшими и в историческом плане первыми видами измерений, например, измерение длин линий землемерной лентой или рулеткой.

Косвенные измерения основываются на использовании некоторых математических зависимостей между искомыми и непосредственно измеряемыми величинами. Например площадь прямоугольника на местности определяют, измерив длины его сторон.

Дистанционные измерения основываются на использовании ряда физических процессов и явлений и, как правило, связаны с использованием современных технических средств: светодальномеров, электронных тахеометров, фототеодолитов и т. д.

На точность проводимых измерений влияют ряд факторов и условий: сам объект измерений, используемые единицы измерений, технические средства, технология и методы производства работ, состояние окружающей среды, опыт производителей работ и т. д. В связи с этим измерения, производимые в условиях, при которых все получаемые результаты можно считать одинаково надежными, называют равноточными и, наоборот, когда результаты нельзя считать одинаково надежными — неравноточными.

Поскольку геодезические работы предполагают прежде всего измерения, то последние производятся с неизбежными погрешностями. При многократном измерении одной и той же величины каждый раз получают несколько отличающиеся результаты как по абсолютной величине, так и по знакам, каким бы опытом не обладал исполнитель и какими бы высокоточными приборами он не пользовался.

Погрешности различают: грубые, систематические и случайные.

Появление грубых погрешностей связано с серьезными ошибками и промахами при производстве измерительных работ. Поскольку обязательным принципом производства геодезических работ является контроль основных геодезических действий, то грубые погрешности сравнительно легко выявляются и устраняются.

Заранее определимы и могут быть сведены к необходимому минимуму путем введения соответствующих поправок

и систематические погрешности.

Например, заранее может быть учтено влияние кривизны Земли на точность определения вертикальных расстояний, влияние температуры воздуха и атмосферного давления при определении длин линий светодальномерами или электронными тахеометрами, заранее можно учесть влияние рефракции атмосферы и т. д.

Если не допускать грубых погрешностей и устранять систематические, то качество измерений будет определяться только случайными погрешностями, которые неустранимы, однако их поведение подчиняется законам больших чисел, поэтому их можно анализировать, контролировать и сводить к необходимому минимуму. Для уменьшения влияния случайных погрешностей на результаты измерений прибегают к многократным измерениям, к улучшению условий

работы, выбирают более совершенные приборы, методы измерений и осуществляют тщательное их производство.

Сопоставляя ряды случайных погрешностей равноточных измерений можно обнаружить, что они обладают следующими свойствами:

а) для данного вида и условий измерений случайные погрешности не могут превышать по абсолютной величине некоторого предела;

б) малые по абсолютной величине погрешности появляются чаще больших;

в) положительные погрешности появляются так же часто, как и равные им по абсолютной величине отрицательные;

г) среднее арифметическое из случайных погрешностей одной и той же величины стремится к нулю при неограниченном увеличении числа измерений.

Поведение случайных погрешностей в ряду равноточных измерений (их свойства) подчиняется закону нормального распределения Гаусса, графическое изображение которого представлено на рис. 6.1.

Если обозначить точное значение какой-либо величины через X, а ее измеренное значение через l, то абсолютная величина случайной погрешности и ее знак определятся разностью: ∆ = l - X. (6.1)

Разность между результатом измерения некоторой величины l и ее истинным значением Х называют абсолютной (истинной) погрешностью.

Абсолютная погрешность не является, однако, исчерпывающе полным показателем точности выполненных работ. Например, если некоторая линия, фактическая длина которой составляет 1000 м, измерена землемерной лентой с ошибкой 0,50 м, а отрезок длиною 200 м — с ошибкой 0,20 м, то, несмотря на то, что абсолютная погрешность первого измерения больше второго, все же первое измерение было выполнено с точностью в два раза более высокой. Поэтому необходимо ввести понятие относительной погрешности: .

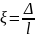Отношение абсолютной погрешности измеряемой величины ∆ к самой этой величине l называют относительной погрешностью.

Относительные погрешности е всегда выражаются дробью с числителем, равным единице. Так, в приведенном выше примере относительная погрешность первого измерения составляет 1/2000, а второго—1/1000.

АРИФМЕТИЧЕСКОЕ СРЕДНЕЕ

Если выполнен ряд равноточных измерений одной и той же величины (l₁, l₂,…, l_n) и нет оснований для того, чтобы отдавать предпочтение одному из них, то, согласно последнему свойству случайных погрешностей, за окончательное значение измеренной величины следует принять среднее арифметическое результатов всех измерений:

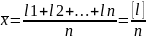(6.3)

В формуле (6.3) сумма в числителе обозначена квадратными скобками, как это принято в теории погрешностей по Гауссу.

Поскольку X есть истинное значение измеряемой величины, можно вычислить ряд соответствующих абсолютных погрешностей измерений: ∆₁=Х-l₁; ∆₂ =Х-l₂;...; ∆_n =Х-l_n (6.4)

Сложив правые и левые части уравнений (6.4), получим ,

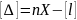Откуда (6.5)

Как следует из формулы (6.5), с увеличением числа измерений 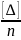будет стремиться к нулю и, следовательно,

при бесконечно большом числе измерений средняя арифметическая величина будет равна истинному значению Х.

Поскольку на практике число измерений все же ограничено, то среднее арифметическое 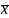будет несколько отличаться от истинного значения измеряемой величины X, однако при всяком п арифметическое среднее считают более надежным значением измеряемой величины.

СРЕДНЯЯ КВАДРАТИЧЕСКАЯ ПОГРЕШНОСТЬ ИЗМЕРЕНИЙ. ПРЕДЕЛЬНАЯ ПОГРЕШНОСТЬ

Для оценки степени точности ряда измерений одной и той же величины недостаточно знать арифметическое среднее погрешностей измерений, которое не является исчерпывающим показателем качества измерительных работ. Это связано прежде всего с тем, что при определении арифметического среднего в ряде измерений может быть не отражено наличие

сравнительно крупных погрешностей разных знаков, поскольку последние взаимно компенсируются.

В связи с этим Гаусс предложил КРИТЕРИЙ ОЦЕНКИ ТОЧНОСТИ, не зависящий от знаков отдельных сравнительно крупных погрешностей ряда — среднюю квадратическую погрешность измерений. Средняя

квадратическая погрешность измерений—это корень квадратный из арифметического среднего квадратов истинных погрешностей: 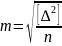(6.6)

Поскольку истинное значение измеряемой величины X не известно, то среднюю квадратическую погрешность т вычисляют по уклонениям о, отдельных результатов измерений l_i от арифметического среднего :

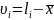
Через уклонения арифметического среднего среднюю квадратическую погрешность определяют по формуле Бесселя:

(6.7)

Этой формулой и пользуются на практике для вычисления величины средней квадратической погрешности измерений.

Анализ кривой нормального распределения Гаусса (см. рис. 6.1) показывает, что при достаточно большом числе измерений одной и той же величины случайная погрешность измерения может быть:

больше средней квадратической т в 32 случаях из 100;

больше удвоенной средней квадратической 2т в 5 случаях из 100;

больше утроенной средней квадратической Зт в 3 случаях из 1000.

Маловероятно, чтобы случайная погрешность измерения оказалась больше утроенной средней квадратической, поэтому утроенную среднюю квадратическую погрешность считают предельной: ∆_пр= Зт. (6.8)

В качестве предельной часто принимают среднюю квадратическую погрешность, равную ∆_пр = 2 , 5т , с вероятностью ошибки, равной порядка 1%.