Хи2обр (вероятность; число степеней свободы)
В данном случае ХИ2ОБР(0.05; 7)=14.06.
Сравниваем найденное значение χ2 с χ2крит. Поскольку χ2 ≤ χ2крит, то гипотезу H0 о совпадении эмпирического распределения с теоретическим принимаем.
.
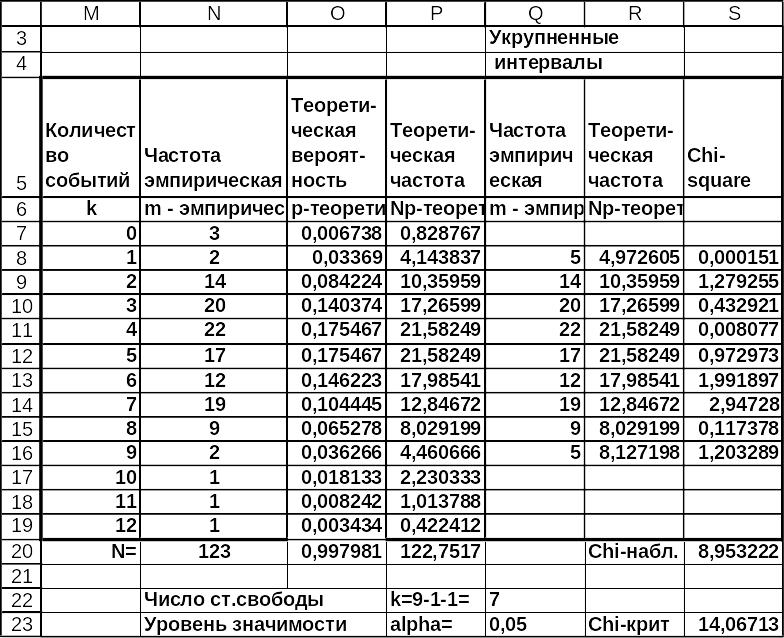
Рис.3.25 Решение примера 1 в MS Excel Решение примера 1 в MS Excel в режиме отображения данных (окончание).
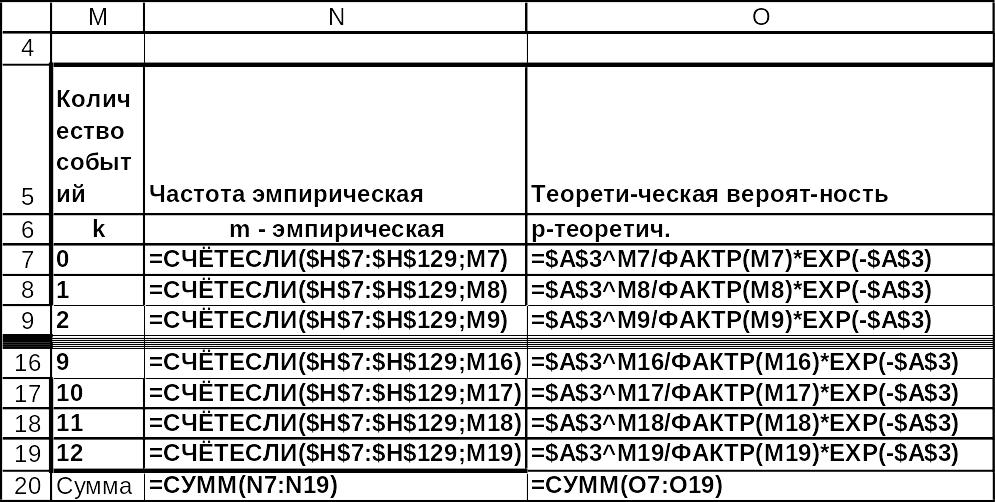
Рис.3.26 Решение примера 1 в MS Excel в режиме отображения формул
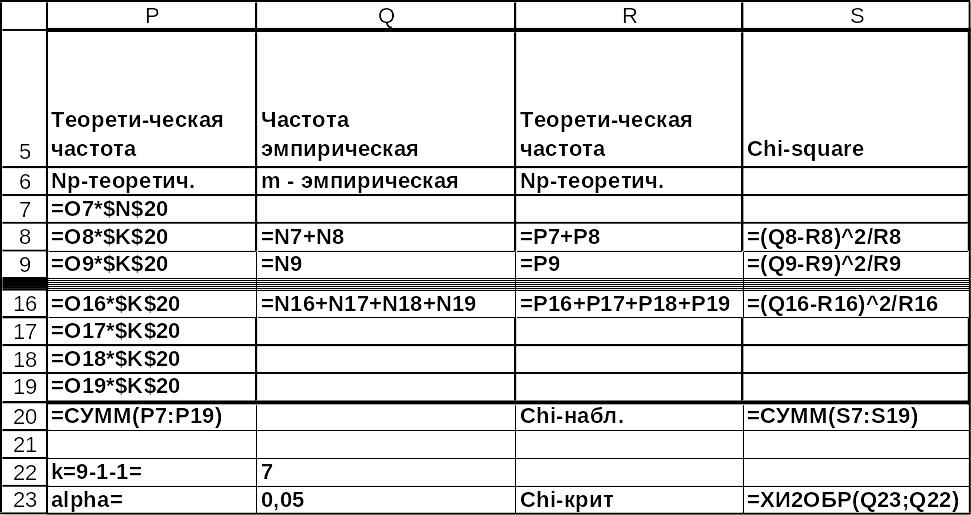
Рис.3.27 Решение примера 1 в MS Excel в режиме отображения формул (окончание).

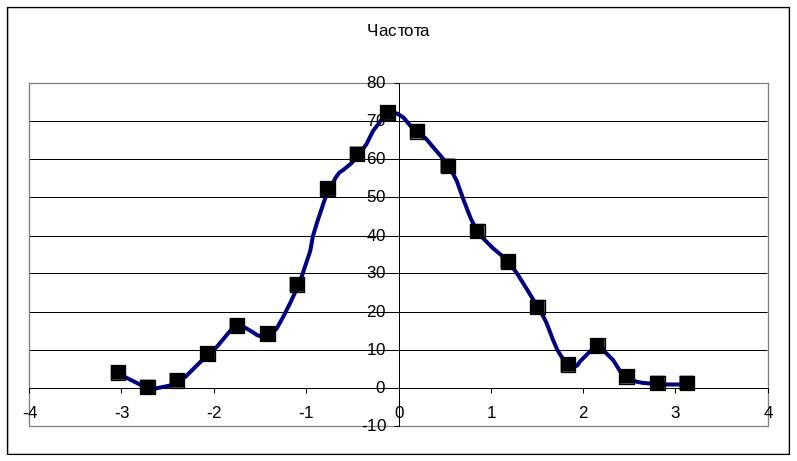
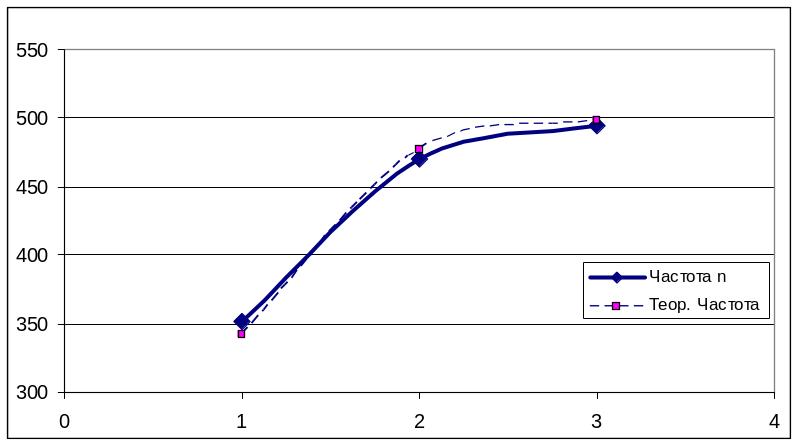
Рис.3.28 График экспериментальных относительных частот и теоретических значений вероятности для примера 1.
Вычисление среднего количества событий в минуту N/Tн за интервал времени Tн.=60, для 7 интервалов времени приведено на рис. 3.29-3.30. Количество событий внутри каждого интервала изменяется от 275 до 302, т.е. оставалось приблизительно постоянным. Все средние значения оказались приблизительно равными и лежащими в интервале от 4.58 до 5.03. Эти значения оказались несколько меньшими ожидаемой интенсивности потока , равной 5 Это можно объяснить случайным характером процесса имитационного моделирования. Полученная картина распределения количества наблюдений за достаточно продолжительный интервал является иллюстрацией двух основных свойств простейшего потока событий – стационарности и отсутствия последействия.
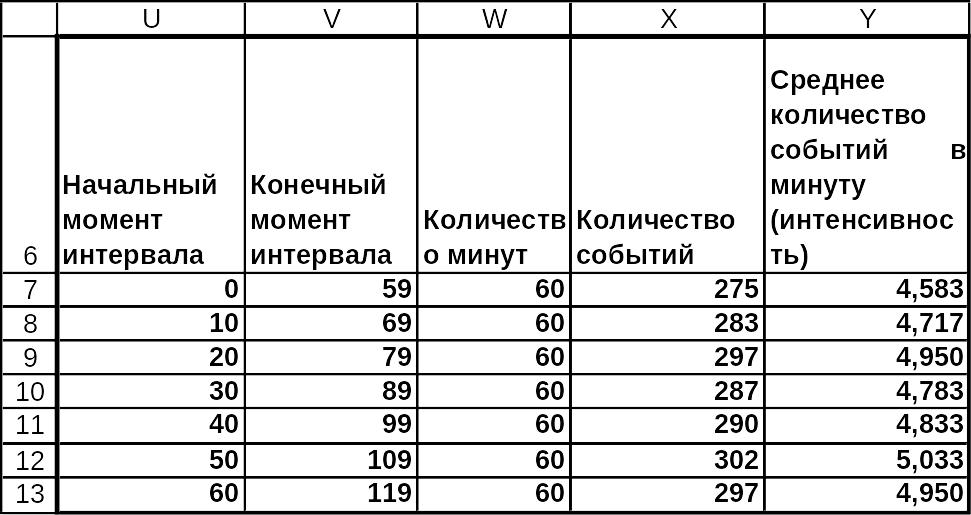
Рис.3.29 Решение примера 1 в MS Excel Решение примера 1 в MS Excel в режиме отображения формул (окончание).
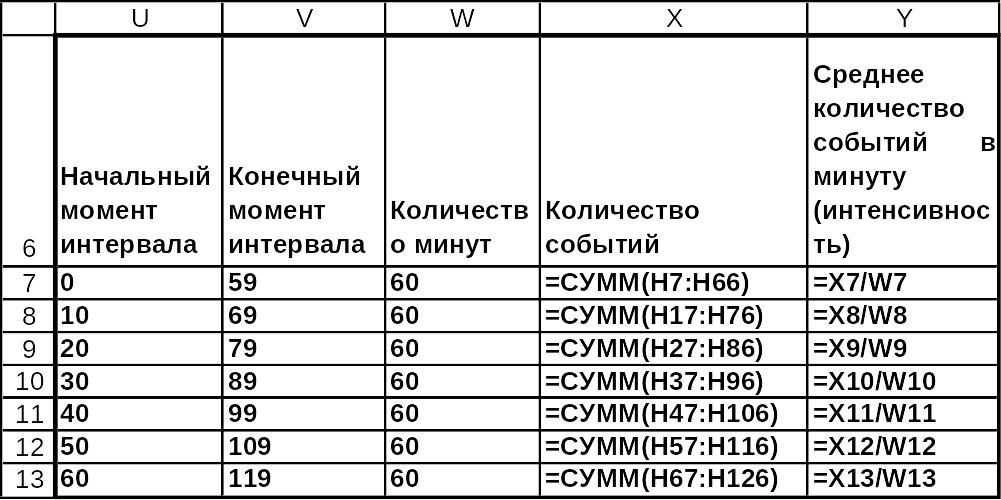
Рис.3.30 Решение примера 1 в MS Excel в режиме отображения формул (окончание).