Пример 4.

Пусть случайная величина X задана следующей таблицей

X	0	1	2
pi	0,6	0,3	0,1

Построить имитационную модель, моделирующую реализацию данной СВ.

Решение: Случайная величина X может принимать следующие значения: х₁=0, х₂=1, , х₃=2.

Чтобы обеспечить реализацию этой случайной величины в MS Excel используем функцию СЛЧИС(), которая вычисляет значения равномерно распределенной случайной величины в интервале [0;1]. Пусть число является значением функции СЛЧИС(), тогда величина , вычисленная по правилу

будет иметь искомое распределение.

Геометрическая иллюстрация этой формулы приведена на рис.4.1. Здесь существенно использовано, то, что длина каждого из интервалов равна заданной вероятности.

Условное выражение с возможностью выбора из трех вариантов в MS Excel можно реализовать с помощью вложенной функции ЕСЛИ(). Однако это решение не рационально, поскольку его реализация становится громоздкой в случае большего количества вариантов выбора. Воспользуемся функцией ВПР().

Синтаксис

ВПР(искомое_значение, таблица, номер_столбца)

Аргументы (Аргумент. Значение, предоставляющее информацию для действия, события, метода, свойства, функции или процедуры.) функции ВПР описаны ниже.

• Искомое_значение Значение, которое должно быть найдено в первом столбце таблицы или диапазона. Аргумент искомое_значение может быть значением или ссылкой. Если искомое_значение меньше, чем наименьшее значение в первом столбце аргумента таблица, функция ВПР возвращает значение ошибки #Н/Д.

• Таблица Диапазон ячеек, содержащий данные. Можно использовать ссылку на диапазон (например, A2:D8) или имя диапазона. Значения в первом столбце аргумента таблица — это значения, в которых выполняется поиск аргумента искомое_значение. Эти значения могут быть текстовыми, числовыми или логическими. Текстовые значения в нижнем и верхнем регистре считаются эквивалентными.

• Номер_столбца Номер столбца в аргументе таблица, из которого возвращается совпадающее значение. Если номер_столбца равен 1, то возвращается значение из первого столбца аргумента таблица; если номер_столбца равен 2, — значение из второго столбца аргумента таблица и т. д.

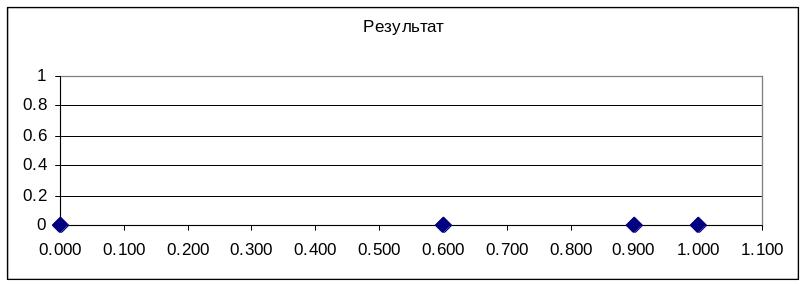
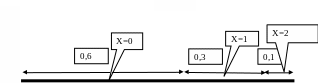
Рис.4.1.

Решение приведено на рис.4.2.

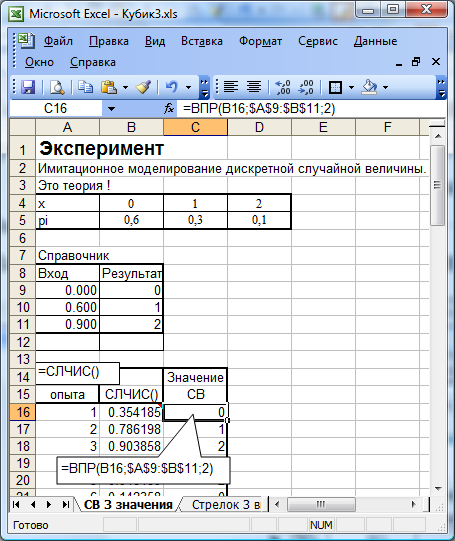
Рис.4.2.

Все остальные расчеты аналогичны примерам 1 и 2.

Пример 5.

Пусть стрелок стреляет в мишень, координаты центра которой совпадает с началом координат. Мишень имеет три зоны - три концентрических окружности с радиусами равными 1, 2 и 3. Провести имитацию стрельбы, полагая, что точка прицеливания это центр мишени, а точка попадания определяется двумя непрерывными СВ X и φ. Первая величина определяет расстояние, на которое удалена точка попадания от точки прицеливания, вторая величина φ равна углу между направлением оси ОХ и направлением на точку попадания.

П

r

y

ри этом будем полагать, что эта величина X имеет нормальное распределение с параметрами m ,σ , т.е. X~N(m ,σ). Расстояние от точки прицеливания до точки попадания равно . Будем считать, что m=0 и σ =1, т.е. величина X имеет стандартное нормальное распределение.

Будем также полагать, что величина φ имеет равномерное распределение в интервале

Построить имитационную модель, моделирующую процесс многократной стрельбы. Вычислить количество попаданий в каждую из зон мишени, их долю от общего количества повторений. Найти среднее значение величины X (расстояние с учетом знака!) попаданий и средний разброс относительно среднего.

Построить интервальный вариационный ряд.

Для этого разбить диапазон экспериментальных значений на n_int=20 частей.

Построить график.

Расчет провести в MS Excel, повторив имитацию не менее 500 раз. Сравнить полученные результаты с соответствующими теоретическими характеристиками.