1. Титульный лист

2. Вставка рисунков из MS EXCEL

3. Аннотация

4. Формулы – жирнение, выравнивание, нумерация (5.30)

5. Заголовок раздела сравнить с частью 1

6. Формулировка заданий лаб.раб5

7. Коэффициент детерминированности- обозначение в лр5 и лр6

Санкт-Петербургский государственный горный институт им Г.В. Плеханова

(технический университет)

Кафедра информатики и компьютерных технологий

Эконометрика

ПАРНАЯ РЕГРЕССИЯ

Методические указания для выполнения лабораторных работ

для студентов специальности 080109 «Бухгалтерский учет, анализ и аудит»

САНКТ-ПЕТЕРБУРГ

2008

Федеральное агентство по образованию

Санкт-Петербургский государственный горный институт им Г.В. Плеханова

(технический университет)

Кафедра информатики и компьютерных технологий

Эконометрика

ПАРНАЯ РЕГРЕССИЯ

Методические указания для выполнения лабораторных работ

для студентов специальности 080109 «Бухгалтерский учет, анализ и аудит»

САНКТ-ПЕТЕРБУРГ

2008

УДК 519.86:622.3.012 (075.83)

ЭКОНОМЕТРИКА. Парная регрессия.

Методические указания для выполнения лабораторных работ для студентов специальности 080109. /СПГГИ(ТУ). Сост.: В.В. Беляев , Т.А. Виноградова, Т.Р. Косовцева. СПб, 2008., ХХ с.

Методические указания содержат необходимые теоретические сведения по выполнению лабораторных работ по эконометрике. Приведены необходимые теоретические сведения и примеры выполнения заданий по исследованию корреляционных и регрессионных связей между характеристиками экономического процесса, которые являются теоретической основой применения эконометрических методов. Все решения выполнены с использованием электронных таблиц MS Excel, в том числе с применением надстройки «Пакет анализа».

Методические указания предназначены для студентов специальности «Бухгалтерский учет, анализ и аудит» дневной формы обучения.

Табл.X. Рис.XX. Библиогр.: X назв.

Научный редактор - ст.преп. Быкова Е.В.

© Санкт-Петербургский государственный горный институт им. Г.В.Плеханова, 2008 г.

Введение

Эконометрика – наука о применении статистических методов в экономическом анализе для проверки правильности экономических теоретических моделей и способов решения экономических проблем.

Основной целью эконометрики является модельное описание конкрет­ных количественных взаимосвязей, обусловленных общими качественными за­кономерностями, изученными в экономической теории.

Области применения эконометрических моделей напрямую связаны с целями эконометрического моделирования, основными из которых являются:

1) анализ экономических и социально-экономических показателей, характеризующих состояние и развитие анализируемой системы;

2) прогноз различных возможных сценариев социально-экономического развития анализируемой системы.

В качестве анализируемой экономической системы могут выступать страна в целом, регионы, отрасли и корпорации, а также предприятия, фирмы и домохозяйства.

Одним из основных типов экономических моделей являются регрессионные модели с одним уравнением. Простейшей моделью является парная регрессия, т.е. модель в которой анализируется взаимосвязь между двумя величинами. В этих работах рассматриваются способы исследования взаимосвязи между переменными с помощью линейной и нелинейной регрессии и корреляции. Параметры регрессии оценивают уравнение регрессии, которое описывает взаимосвязь, а параметры корреляции оценивают силу этой взаимосвязи.

Лабораторная работа 5. ЛинЕная регрессия.

Цель: освоить на практике нахождение с помощью табличного процессора MS EXCEL числовых характеристик линейной парной регрессии, а также изучить основные свойства теории корреляции.

5.1. Теоретические сведения

Рассмотрим некоторый экономический объект (процесс, явление, систему) и выделим только две признака (величины), характеризующие этот объект. Обозначим признаки буквами Y и X.

Тесноту линейной связи между признаками Y и X характеризует коэффициент корреляции :

, (5.1)

где величина называется ковариацией между признаками Y и X,

;

.

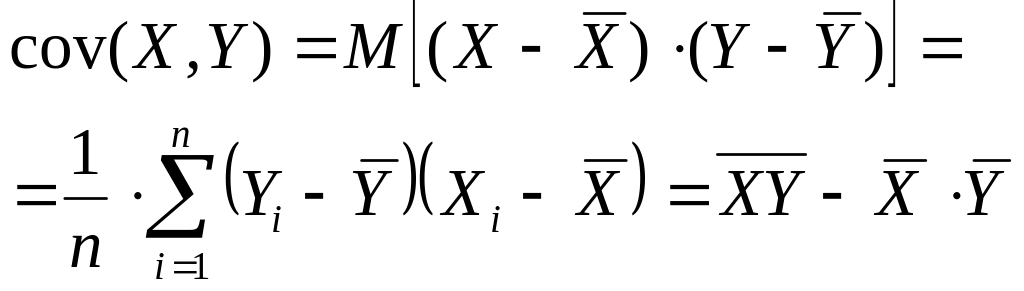Отметим, что . Чем ближе к единице, тем сильнее связь. Если , то между признаками и существует прямая зависимость, т.е. с ростом одного признака другой признак тоже возрастает. Если , то между признаками и существует обратная зависимость, т.е. с ростом одного признака другой признак убывает. Если , то между признаками и существует линейная зависимость. Если , то между признаками и отсутствует линейная зависимость.

Иногда показателям тесноты связи можно дать качественную оценку (шкала Чеддока) (табл.5.1).

Таблица 5.1

Количественная мера тесноты связи	Качественная характеристика силы связи
0,1-0,3	Слабая
0,3-0,5	Умеренная
0,5-0,7	Заметная
0,7-0,9	Высокая
0,9-0,99	Весьма высокая

Следует отметить, что при вычислении коэффициента корреляции оба признака и входят симметрично (равноправно), т.е. он характеризует как зависимость от , так и зависимость от .

Будем предполагать, что независимая переменная X (объясняющая переменная, предиктор, факторный признак, регрессор) оказывает воздействие на значения зависимой переменной Y (отклик, результативный признак), т.е. имеет место зависимость:

(5.2)

Зависимость (5.2) можно рассматривать с целью установления самого факта наличия или отсутствия значимой связи между Y и X, можно преследовать цель прогнозирования неизвестных значений Y по известным значениям X, наконец, возможно выявление причинно-следственных связей между X и Y. Таким образом, уравнение регрессии позволяет провести анализ и прогноз.

Пусть мы располагаем п- парами выборочных наблюдений над двумя переменными X и Y:

(5.3)

Функция f(X) называется функцией регрессии Y на X, если она описывает изменение значений результирующей переменной Y в зависимости от изменения значений объясняющей переменной Х. Таким образом, имеет место уравнение регрессионной связи между Y и X:

(5.4)

Присутствие в модели (5.4) случайной компоненты _i, называемой случайным членом или возмущением, обусловлено следующими причинами:

• ошибками спецификации, то есть отбора факторов и выбора связи между явлениями;

• ошибками измерения;

• ошибками, связанными со случайностью человеческих реакций.

Относительно  необходимо принять ряд гипотез, известных как условия Гаусса-Маркова:

1. Равенство нулю математического ожидания случайного члена:

2. Постоянство дисперсии регрессионных остатков (гомоскедастичность остатков):

3. Отсутствие систематической связи (корреляции) между значениями случайного члена в любых двух наблюдениях:

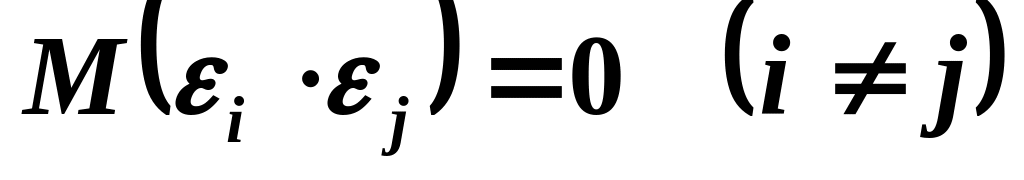
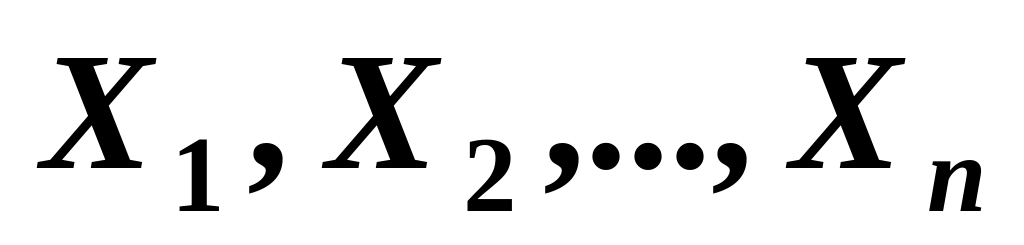4. - неслучайные величины.

Уравнение линейной регрессии

(5.5)

В данной работе - теоретические значения отклика. Коэффициент в уравнении (5.5) называется коэффициентом регрессии. Его величина показывает среднее изменение результата при изменении фактора на единицу. Параметр может и не иметь экономического смысла, формально это значение функции при нулевом значении параметра . Для определения коэффициентов уравнения (5.5) используется метод наименьших квадратов (МНК).

.

Рис.5.1 Геометрический смысл метода наименьших квадратов.

Рассмотрим сумму

, (5.6)

она равна сумме квадратов отклонений. Величина этой суммы зависит от коэффициентов и . Суть метода наименьших квадратов (МНК) заключается в выборе таких оценок и , для которых сумма квадратов отклонений (остатков) найденных значений функции (5.5) от заданных значений функции (5.3) для всех точек будет минимальной.

Для того чтобы найти набор коэффициентов и , которые доставляют минимум функции , определяемой формулой (5.6), используем необходимое условие экстремума функции нескольких переменных - равенство нулю частных производных. В результате получим нормальную систему для определения коэффициентов и :

(5.7)

После преобразования систему (5.7) можно привести к виду

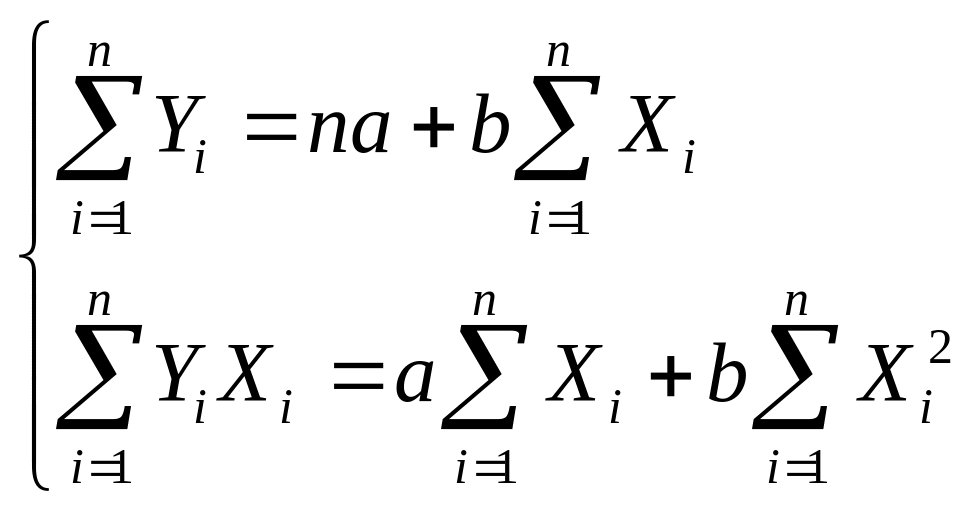(5.8)

Таким образом, нахождение коэффициентов и сводится к решению системы линейных уравнений относительно и . Эту систему можно решить различными способами: с помощью обратной матрицы, по формулам Крамера, методом Гаусса, методом подстановки. Решая последним способом, получаем соотношения

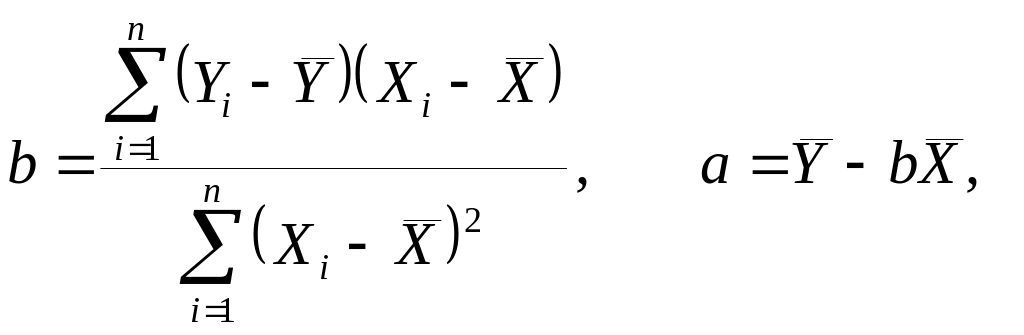(5.9)

Таким образом, коэффициенты и линейного уравнения парной регрессии можно получить по формулам (5.9)