Пример 3

Упростить игру (Рис. 5.25), решить ее графически и найти точное решение.

	В1	В2	В3	В4
А1	1	2	4	3
А2	0	2	3	2
А3	1	2	4	3
А4	4	3	1	0

Рис. 5.25

Решение.

Упрощаем:

1. A₁ совпадает с A_3, поэтому одну из них (например, A₃) можно вычеркнуть;

2. A₁ доминирует A₂, поскольку все элементы A₂ меньше или равны соответствующим элементам A_1, Следовательно, стратегия A₂ заведомо не выгодна, поэтому A₂ можно вычеркнуть. В результате этих действий платежная матрица примет вид, приведенный на Рис. 5.26.

Рассматривая последнюю платежную матрицу, заметим, что можно провести следующее упрощение:

B₄ доминирует B₃, поэтому B₃ можно вычеркнуть (именно так, поскольку В₃ заведомо не выгодна для игрока В).

Таким образом, платежная матрица принимает следующий вид (Рис.5.27), ее размерность 2х3, и для решения такой игры применим графический метод.

	B1	B2	B3	B4
A1	1	2	4	3
A4	4	3	1	0

Рис. 5.26

	B1	B2	B4	ai
A1	1	2	3	1
A4	4	3	0	0
bj	4	3	3

Рис. 5.27

Верхняя цена игры , нижняя цена . Поскольку , решение ищем в смешанных стратегиях.

Пусть X₀=(p₁,p₄)  оптимальная стратегия игрока A.

Строим линии соответствующие оптимальным стратегиям игрока А (Рис. 5.28) против чистых стратегий игрока В. Ломанная LMN – есть нижняя граница выигрыша, точка M определяет наибольший выигрыш игрока A.

Координата p₁ точки M определяется системой

Решение этой системы .

Цена игры .

Для игрока B решение строится из следующих соображений. Из построения на рисунке (Рис. 5.20) видно, что его активными стратегиями являются B₁ и B₄, поскольку именно их пересечение определяет точку M.

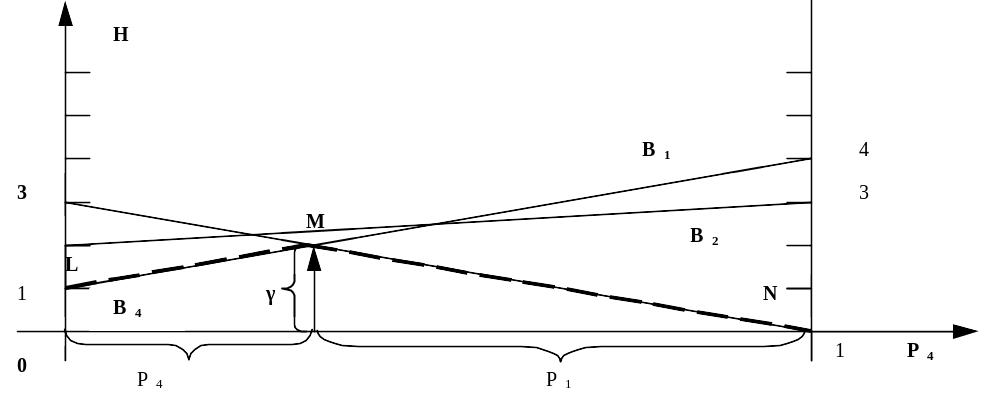
Рис. 5.28

Следовательно, рассматриваемую игру можно свести к игре с платежной матрицей 22 (Рис. 5.29).

	B1	B4
A1	1	3
A4	4	0

Рис. 5.29

Решение такой игры полностью аналогично решению примера 1.

Для того, чтобы найти q₁,q₄, имеем систему:

,

Откуда q₁=0.5 , q₄=0.5 .

Так как стратегии B₂ и B₃ не активна, то q₂=0 , q₃=0 .

Окончательное решение выписывается для исходной матрицы (Рис.5.25), поэтому вспоминаем о стратегиях А₂ и А₃, которые не активны, поэтому p₂=0, p₃=0. Таким образом, получаем окончательный ответ: .