Пример 2. (Переработано из: [4])

Менеджер ресторана, расположенного на одном из тропических островов, заказывает на материке партию мороженного раз в неделю. Многолетний опыт показывает, что возможный объем реализации продукта меняется в диапазоне от 0 до 3 упаковок, в зависимости от погоды. Возможные состояния погоды (природы) можно характеризовать терминами «холодно», «прохладно», «тепло» и «жарко», при этом спрос на мороженное равен 0, 1, 2 и 3 упаковок соответственно. Если продукт не реализован в течение недели, то он подлежит утилизации.

Пусть цена продажи каждой упаковки равна 100 у.е., цена закупки - 40 у.е., неудовлетворенный спрос (упущенная выгода) - 50 у.е. , цена утилизации - 7 у.е.

Определить оптимальный объем закупок, если состояния погоды «холодно», «прохладно», «тепло» и «жарко» реализуются с вероятностями 0.1, 0.3, 0.4 и 0.2 соответственно.

Провести анализ устойчивости решения, полагая, что упущенная выгода меняется от 0 до 150.

Решение

Принимая во внимание, что решение менеджер принимает регулярно, то наиболее рационально рассматривать ситуации, как игру с природой, взяв в качестве критерия выбора решения критерий среднего выигрыша. Решение приведено на рис. 6.29. Ячейки платежной матрицы заполнены значениями платежей, которые вычисляются по формуле

,

где - количество закупленных упаковок;

- количество проданных упаковок;

- неудовлетворенный спрос;

- количество нереализованных упаковок.

Величина среднего выигрыша для каждого варианта содержится в интервале ячеек F9:F12. Максимальное значение среднего выигрыша равное 56.5 у.е., которое соответствует объему закупок в 2 упаковки.

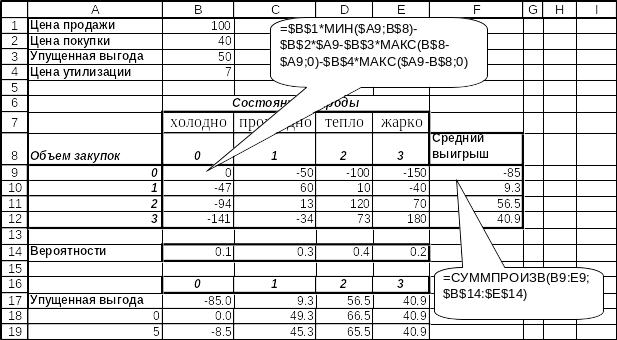
Рис. 6.29.

Решение базируется на объективных значениях цен продажи, закупки и утилизации и на субъективном значении неудовлетворенного спроса, которое определяется менее точно. Проведем анализ чувствительности относительно этого параметра модели.

Анализ чувствительности можно провести, задавая различные значения упущенной выгоды. Для каждого значения необходим пересчет элементов платежной матрицы, вычисление средних выигрышей и выбор на их основе нового оптимального решения.

Воспользуемся средством «Таблица подстановки», выполнив для этого следующие действия:

Заполним значениями 0 от до 150 с шагом равным 5 интервал ячеек А18:А48;

В диапазон ячеек B17:E17 введем формулы =F9 …=F12 (рис.6.30);

Выделим диапазон А17:Е48 и вызовем средство «Таблица подстановки», которое содержится в пункте меню «Данные». В диалоговом окне в поле «Подставлять значения по строкам в» вводим значение $B$3 (рис.6.31). Это обеспечит подстановку значений из столбца А в ячейку В3 (по одному значению за один раз), пересчет формул в диапазоне F9:F12 и заполнение столбцов B,C, D и Е в диапазоне А18:Е48. эти значения и являются значениями, соответствующими значениям среднего выигрыша при соответствующем объеме закупок. Выбор максимального значения среднего выигрыша и соответствующего объема закупок проведем графическим методом рис.6.32-6.33.

Рис. 6.30.

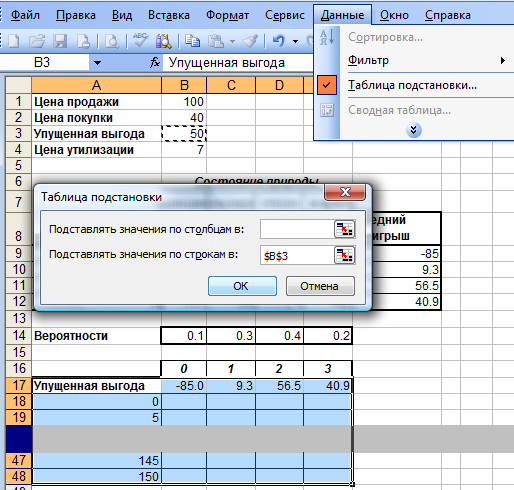
Рис. 6.31.

На графике каждая линия соответствует определенному объему закупок, оптимальному значению соответствует та, которая при заданном значении упущенной выгоды расположена выше. На построенном графике видно, что при возрастании величины упущенной выгоды средний выигрыш убывает (для объемов покупок равным 0, 1 и 2) или остается постоянным для объема покупки в 3 упаковки. На рис.6.33 видно, что если значение упущенной выгоды меньше 127 у.е., то оптимальным будет объем покупки в 2 упаковки. Если значение упущенной выгоды больше 127 у.е., то оптимальным будет объем покупки в 3 упаковки. Окончательно приходим к выводу, что нет необходимости знать точное значение упущенной выгоды – чтобы определить оптимальное решение, достаточно знать будет оно больше или меньше 127 у.е.

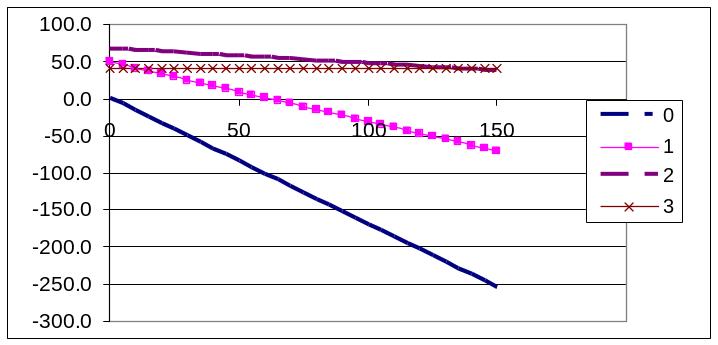
Рис. 6.32.

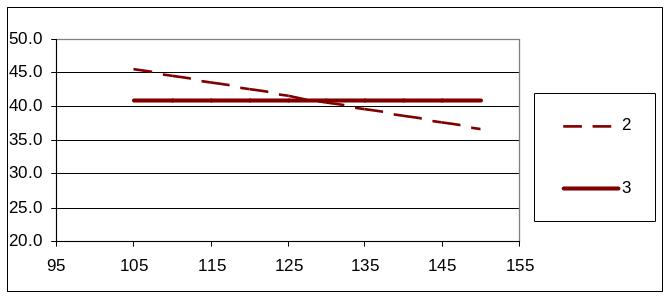
Рис. 6.33.