2.4.3. Интерполирование с использованием MathCad

Как и в случае полинома для произвольных узлов, непосредственное составление в MathCad полинома для равноотстоящих узлов по теоретической формуле также приводит к описанному выше негативному эффекту. Покажем это.

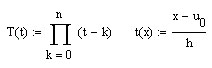
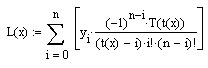
Обратим внимание на выражение . Оно позволяет связать неизвестное и параметр . Поэтому для вычисления в точке уже нет необходимости находить , как это было при ручном счёте.

С учётом негативного эффекта для построения полинома используем программные средства:

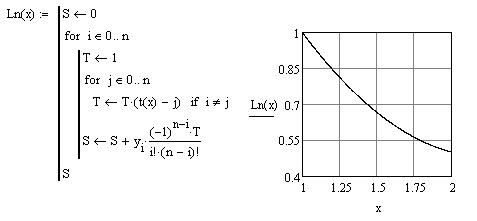
Вычисления дают (сравните с тем, что было выше):

При этом негативного эффекта не возникает:

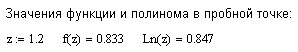
Произведём оценку абсолютной погрешности:

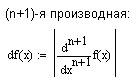
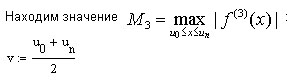
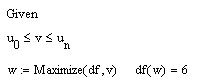
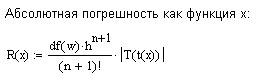
График функции имеет точно такой же вид, что и выше (п. 2.3).

Упражнения

1. Получить в MathCad полиномы Лагранжа для функций:

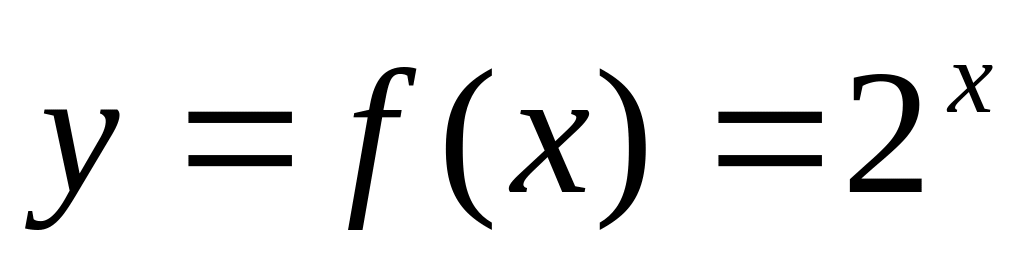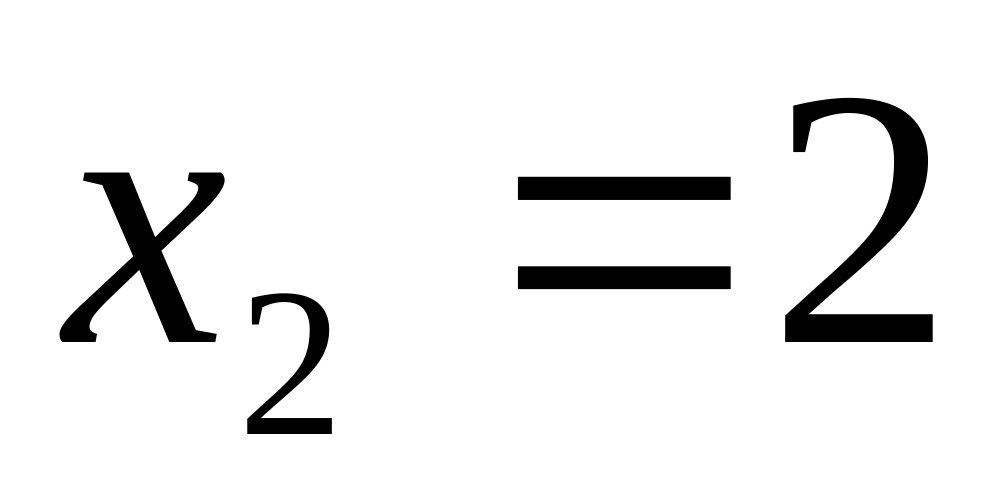   1. с узлами , , ; вычислить точное значение функции, значение полинома и абсолютную погрешность в точке , построить график погрешности;

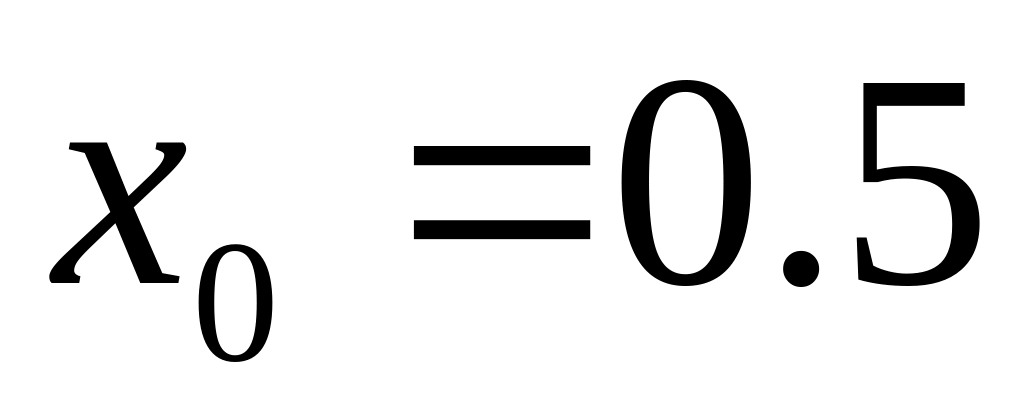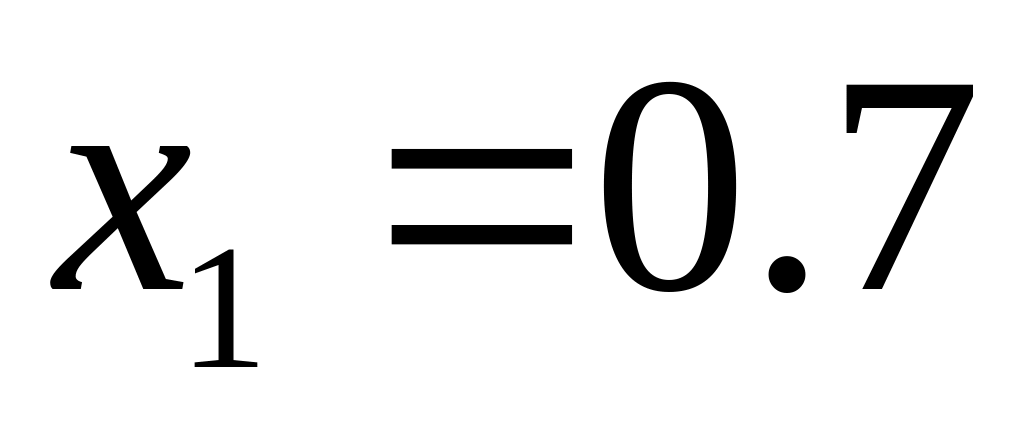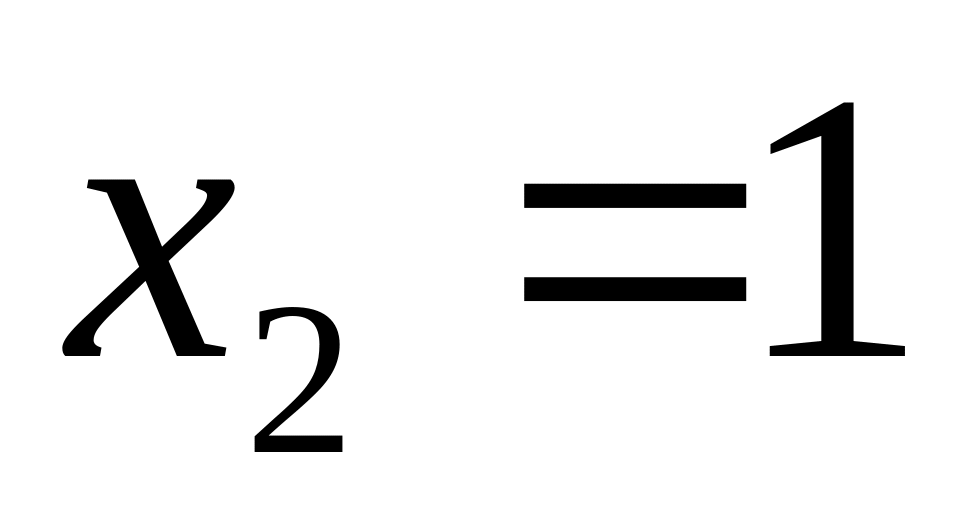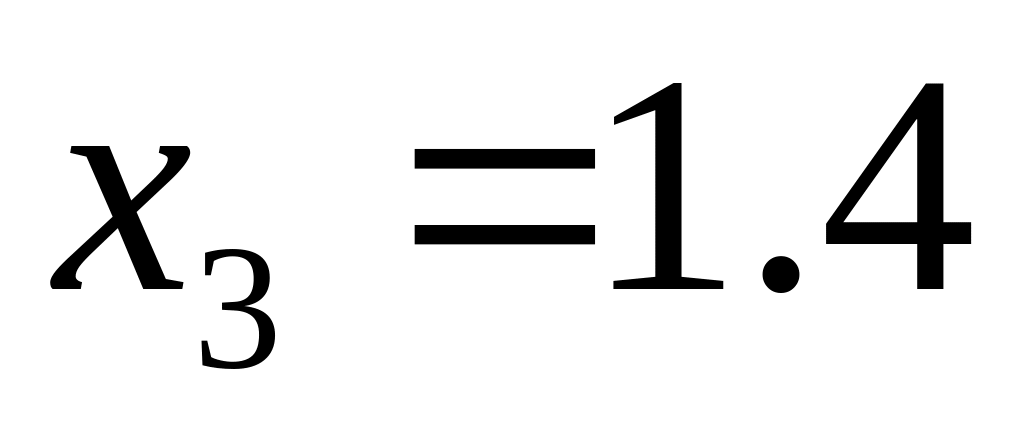   2. с узлами, , , , ; вычислить точное значение функции, значение полинома и абсолютную погрешность в точках 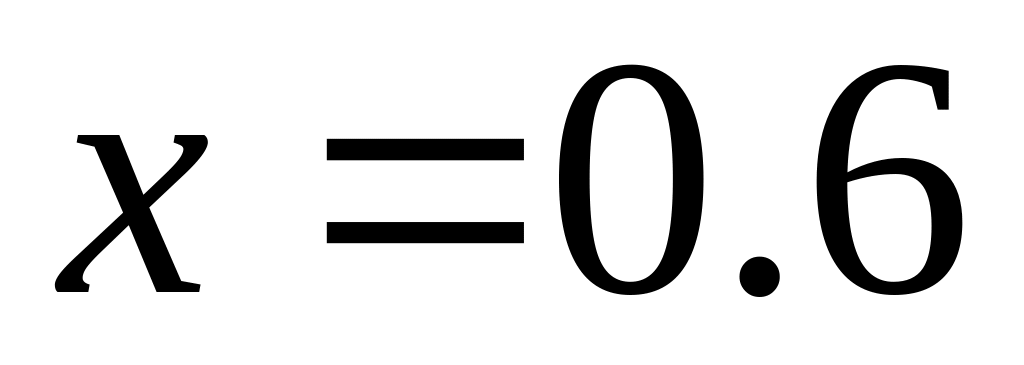, , 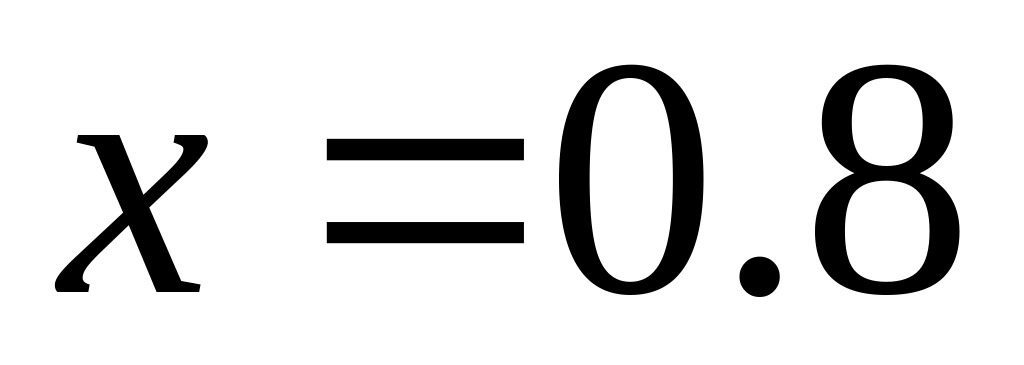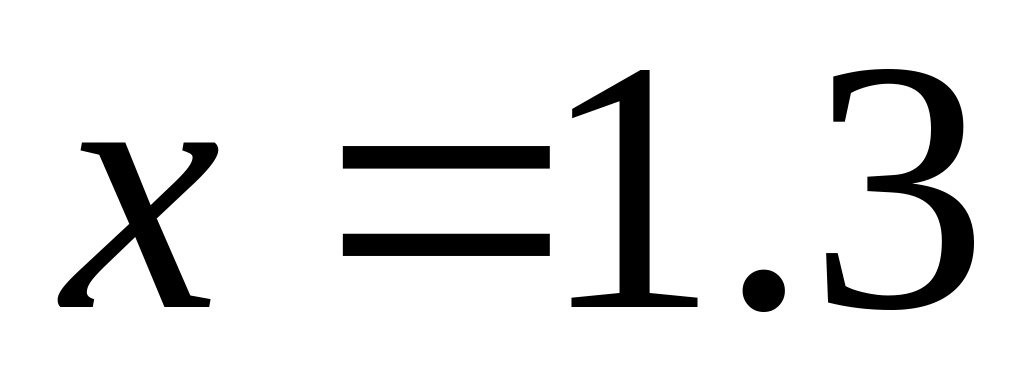; построить график погрешности.

2. Для функции 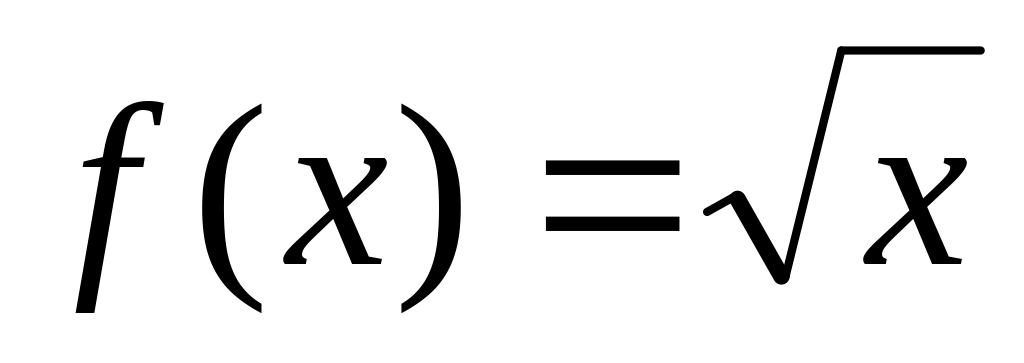на отрезке 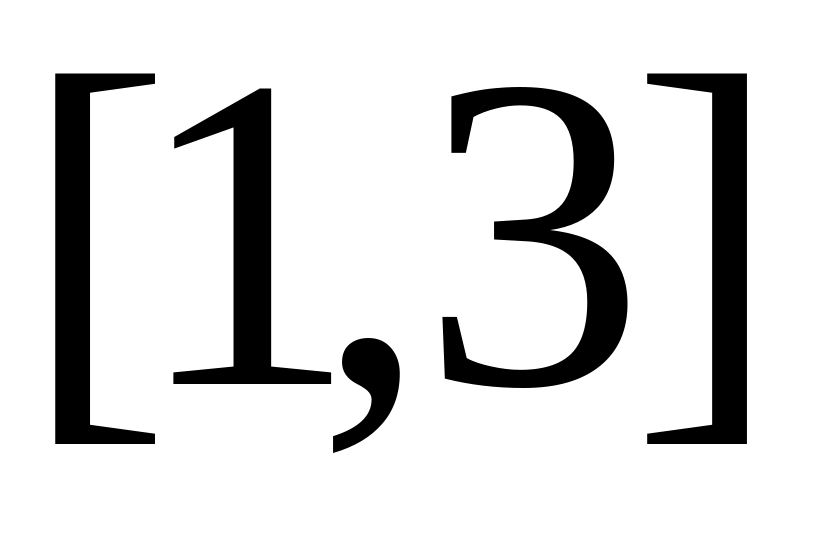построить полиномы Лагранжа для равноотстоящих узлов степени и получить график зависимости границы абсолютной погрешности от значения .

2.5. Полиномы Ньютона для равноотстоящих узлов

2.5.1. Конечные разности

Пусть функция задана таблицей , , с постоянным шагом :

			...		...
			...		...

Число

, ,

называется конечной или табличной разностью первого порядка. Из конечных разностей первого порядка образуются конечные разности второго порядка:

, .

Вообще, разность k-го порядка определяется равенством

.

Полученные разности можно записать в таблицу:

							...
							...
						...
					...
				...
			...
		...
...	...