2) Построение полинома

Исправить положение можно, если использовать для построения полинома программные средства, а именно, организовать цикл накопления произведения с исключением ситуации (продолжаем рабочий лист MathCad):

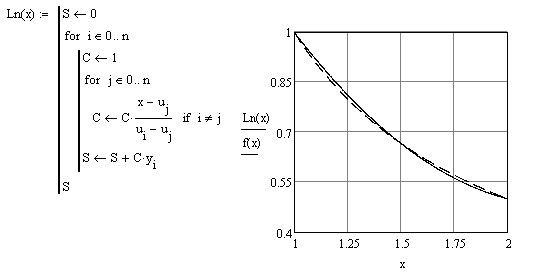
Наложение графиков полинома (сплошная линия) и функции (пунктирная линия) демонстрирует их несовпадение вне узловых точек. Вычисления дают (сравните с тем, что было выше):

При этом негативного эффекта не возникает:

Вычислим абсолютную погрешность.

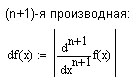
Теперь найдём значение согласно формуле абсолютной погрешности:

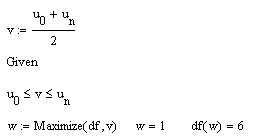
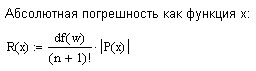
Наложение графиков функций и (они те же самые, см. выше) позволяет увидеть, как образуется погрешность. График функции погрешности имеет характерный вид:

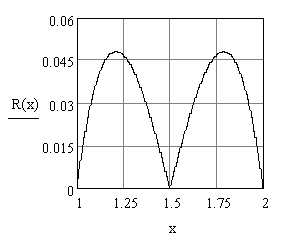
Из графика видно, погрешность в узловых точках равна нулю, но постепенно достигает максимального значения где-то ближе к середине между ними.

Упражнения

Получить в MathCad полиномы Лагранжа для функций:

1. с узлами , , ; вычислить точное значение функции, значение полинома и абсолютную погрешность в точке ;

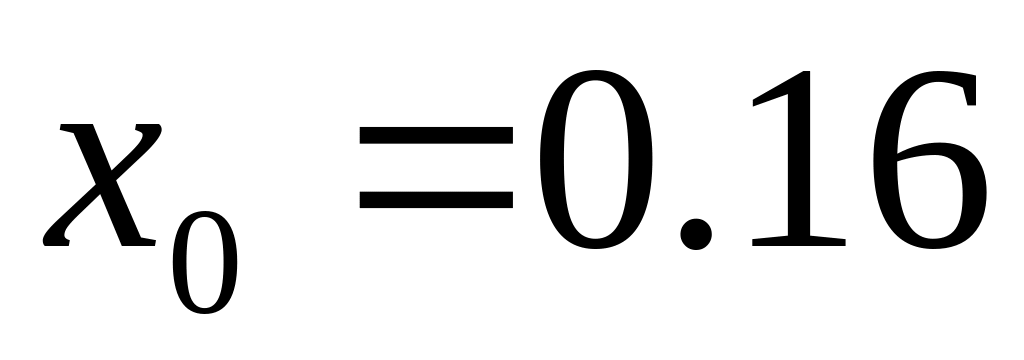2. с узлами , , , ; вычислить точное значение функции, значение полинома и абсолютную погрешность в точке .

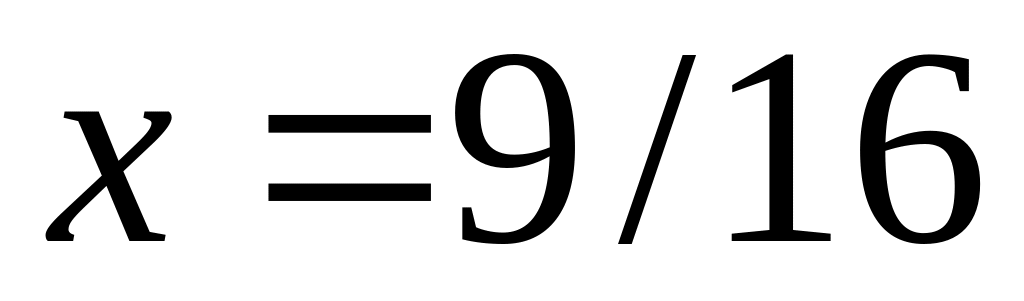2.4. Полином Лагранжа для равноотстоящих узлов

2.4.1. Вывод полинома

Пусть функция задана таблицей , , с постоянным шагом . В этом случае .

Выпишем формулу Лагранжа для произвольных узлов:

,

,

.

Пусть , тогда:

,

,

и т.д.

В общем случае

, .

Тогда

.

При имеем

, .

Выражение разобьём на две части:

.

В 1-й части ровно сомножителей, во 2-ой их , причём знак каждой скобки отрицателен. Для 1-й части имеем:

.

Для 2-й части с учётом для каждого неравенства получим:

.

Собираем выражение:

Таким образом, формула Лагранжа для равноотстоящих узлов имеет вид:

.

Оценку погрешности легко получить из предыдущей подстановкой . В силу единственности интерполяционного полинома можно также пользоваться оценкой для полинома Лагранжа.

2.4.2. Пример ручных вычислений

Составим полином Лагранжа по следующей таблице:

	0	1	2
	1	2	3
	1

Имеем узлы , , и значения функции , , . Шаг таблицы .

Выпишем полином:

.

Подставим данные и вычислим:

.

Сделаем проверку для узла (по основному свойству интерполирования должно выполняться равенство ):

1. так как , то для будет , откуда ;

2. ,

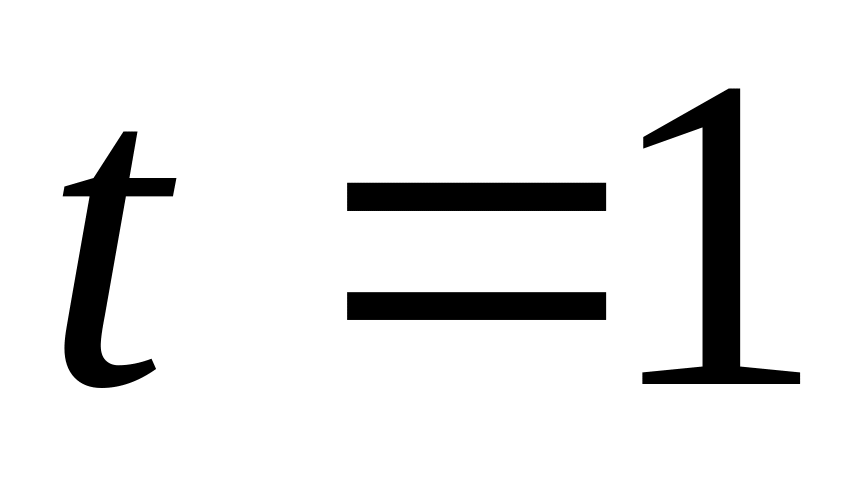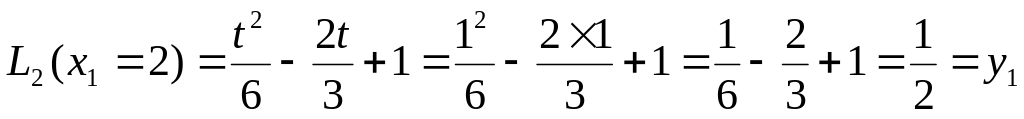результат верный.

Оценим абсолютную погрешность:

.

Найдём все величины:

,

,

.

Таким образом,

.

Вычислим точное значение функции, значение полинома и абсолютную погрешность, например, в точке :

, ,

,

,

.

.

Упражнения

Получить Лагранжа ручным способом для функций:

1. с узлами , 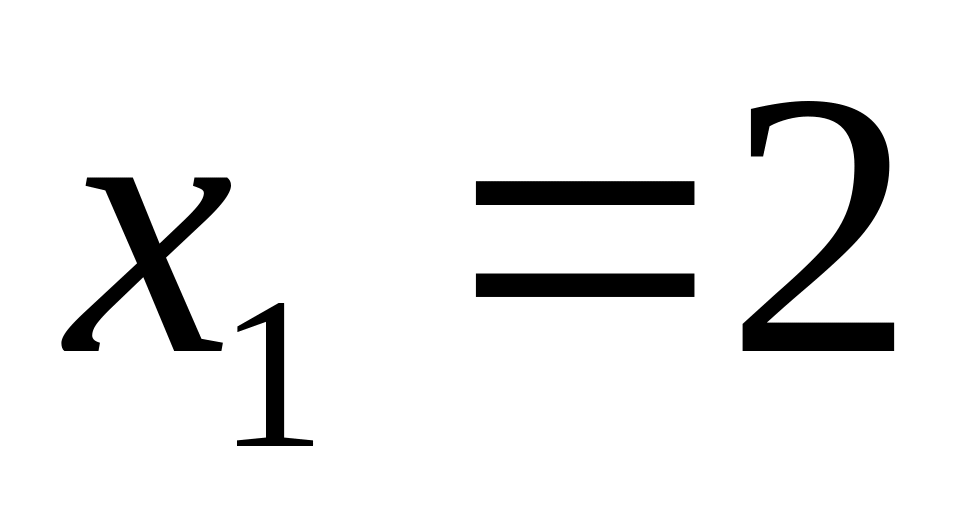, ; вычислить точное значение функции, значение полинома и абсолютную погрешность в точке .

2. с узлами , , ; вычислить точное значение функции, значение полинома и абсолютную погрешность в точке .