2.3. ПосТроение простейшего полинома

Приведённое выше доказательство существования и единственности полинома конструктивно. Это означает, что его можно использовать для построения полинома. Рабочий лист MathCad может выглядеть следующим образом:

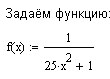
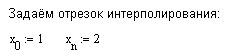
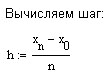
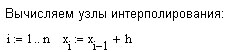
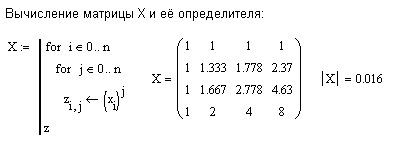
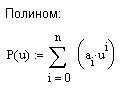
Графики полинома и функции ниже изображены на разных координатных плоскостях, так как при наложении почти сливаются (что говорит о малой для данной функции абсолютной погрешности

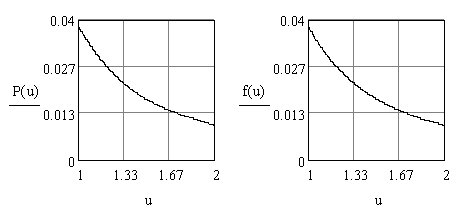
Изменение абсолютной погрешности:

Как будет видно далее, в задачах интерполирования графики абсолютной погрешности имеет именно такой характерный вид. Хорошо видно, что погрешность максимальна между узлами и равна нулю в узлах (последнее есть следствие равенства ). Различие значений максимумов на каждом из промежутков определяется только свойствами интерполируемой функции и длиной промежутков.

Покажем ещё, как вычисляется относительная погрешность (в дальнейшем этого делать не будем):

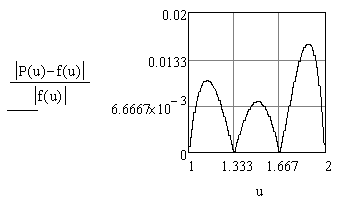
Если функция задана только таблицей своих значений (т.е. её аналитический вид неизвестен), то вместо выражения используют , где – априорная оценка абсолютной погрешности.

Упражнения

1. Построить в MathCad полиномы при 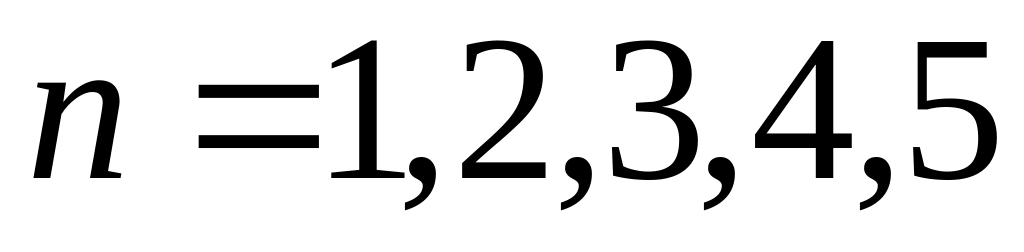и сравнить даваемые ими погрешности для какой-нибудь фиксированной точки из отрезка .

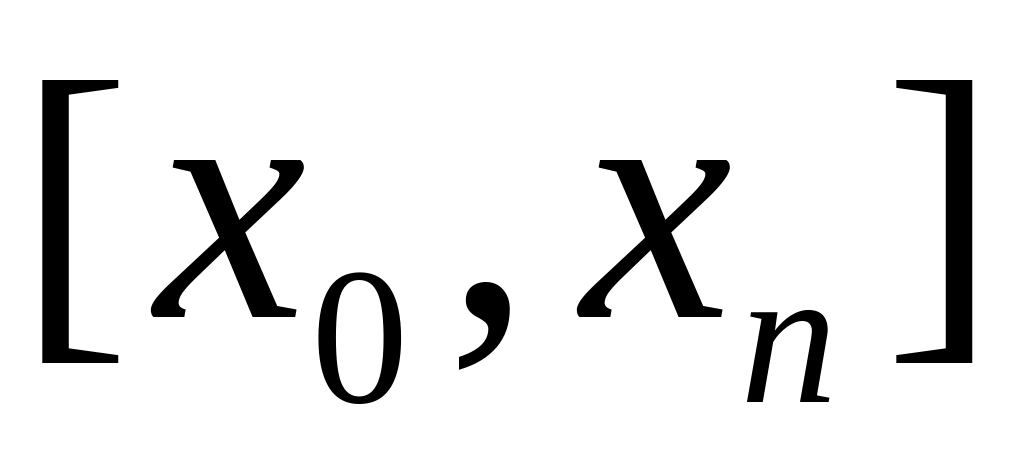2. Для каждого полинома из п.1 построить графики изменения абсолютных погрешностей.

3. Для фиксированной точки из отрезка построить график изменения абсолютной погрешности в зависимости от значения .

2.4. ПосТроение полинома по отрезку ряда Тейлора

Покажем получение аппроксимирующего полинома для функции , допускающей разложение на промежутке в ряд Тейлора. Тогда отрезок ряда

является полиномом степени , и потому аппроксимирует функцию , т.е. . Оценка погрешности аппроксимации вытекает из формулы остаточного члена ряда:

.

Рабочий лист MathCad может выглядеть так.

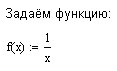
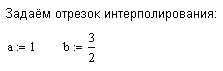
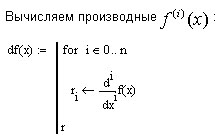
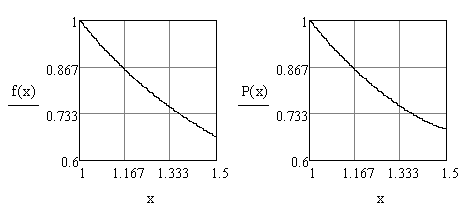
Графики функции и полинома:

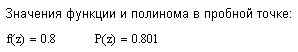
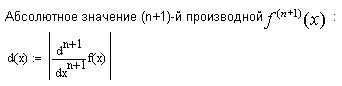
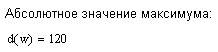
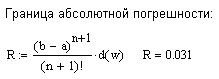
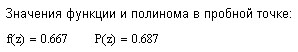
Две пробные точки показывают, что по мере удаления от точки , в окрестности которой функция раскладывалась в ряд, погрешность возрастает, причём ускоренно. Действительно, график погрешности свидетельствует об этом:

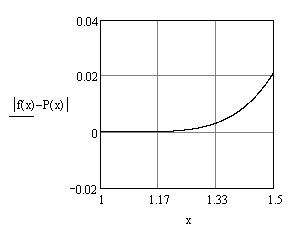
Следовательно, вычисления с помощью ряда Тейлора с точки зрения минимизации погрешности выгодно вести в окрестности точки, в которой функция раскладывается в ряд.

Упражнения

1. Построить в MathCad полиномы по отрезкам ряда Тейлора при 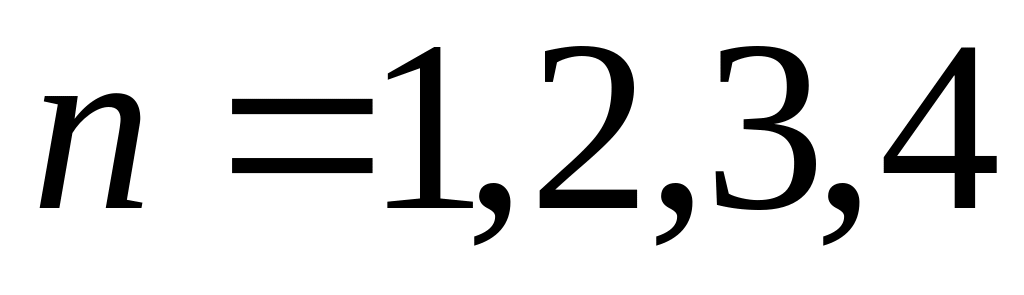и сравнить даваемые ими погрешности для какой-нибудь фиксированной точки из отрезка .

2. Для каждого полинома из п.1 построить графики изменения абсолютных погрешностей.

3. Для фиксированной точки из отрезка построить график изменения абсолютной погрешности в зависимости от значения .

2.3. Полином Лагранжа для произвольных узлов

2.3.1. Вывод полинома

Пусть функция на отрезке задана таблицей своих значений , . Требуется построить полином степени , удовлетворяющий условиям , . Такой полином ищется в виде

,

где – полином степени , который, согласно основному свойству интерполяционного полинома, должен удовлетворять условиям

Будем искать его в виде

,

где коэффициенты подлежат определению.

Обозначим

.

Дифференцируя по как произведение функций, получим

.

При имеем

,

при имеем

и т.д. Значит, при будет

.

Так как , то

.

Теперь с учётом выражения

получаем полином Лагранжа

.

По построению полинома имеем равенство , . Однако в неузловых точках может быть . Исключение составляет лишь случай, когда функция сама является полиномом степени не выше . В этом случае, очевидно, .