2. Интерполирование функций

2.1. Математические таблицы

Пусть функция определена и непрерывна на отрезке . Разделим этот отрезок на часть произвольными точками . Найдём соответствующие значения функции: , ,..., ,..., . Занесём пары точек в таблицу:

			...		...
			...		...

Число называется шагом таблицы, а число называется табличной разностью. Если в таблице , то такая таблица называется таблицей с постоянным шагом. Таблица, содержащая все значения функции с значащими цифрами, называется -значной.

2.2. Постановка ЗадачИ интерполирования

При решении многих задач часто удаётся получить лишь эмпирическую информацию о процессах и явлениях. Как правило, эта информация представляет собой таблицу значений неизвестной функции . Найти явный вид этой функции – дело практически безнадежное. Однако можно подобрать другую, более простую функцию , в некотором смысле близкую к неизвестной. Кроме того, к построению другой функции прибегают и в случаях, когда вычисление значений функции очень трудоёмко, а высокой точности не требуется. С помощью подобранной функции можно приближённо вычислять значения, которые не содержатся в таблице.

Один из способов получения приближённой (часто говорят – приближающей) функции – интерполирование.

Общая постановка задачи такова. Пусть имеется таблица значений функции :

			...		...
			...		...

Требуется построить функцию , принимающую в точках , , те же значения, что и неизвестная функция , то есть должны выполняться равенства (основное свойство интерполирования) , . Функция называется интерполирующей, а точки – узлами интерполирования. Предполагается, что все узлы интерполирования различны, т.е. при .

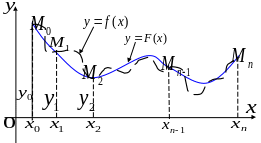
Геометрически интерполирование означает, что нужно найти кривую , проходящую через заданную систему точек , :

В такой постановке задача может иметь бесконечное множество решений или совсем не иметь решения. Однако эта задача становится разрешимой однозначно, если вместо произвольной функции искать полином такой, что , .

Действительно, из последнего равенства вытекает система уравнений

Введя обозначения

, , ,

систему можно записать в матричном виде:

.

Из курса алгебры известно, что данная система однозначно разрешима тогда и только тогда, когда определитель . Определителем матрицы является определитель Ван-дер-Монда

,

который не равен нулю в силу условия при . Следовательно, интерполяционный полином существует и единствен.

Таким образом термины “полином” и “интерполирование” приобретают ясный смысл. А именно, полином (от греч. poly – много и nomos – часть) – это математический объект, составленный из многих частей – одночленов вида , отделенных друг от друга знаками “+” или “–”; интерполирование (от греч. inter – вне и poly – много, а также от лат. interpolatio – изменение, переделка) – это процесс построения аппроксимирующей функции в виде полинома, позволяющего приближённо вычислять значения аппроксимируемой функции вне узлов (или, иначе, между узлами).