2.8.2. Полиномы Чебышёва и их свойства

Полиномы Чебышёва – это последовательность полиномов, которая строится по формулам

, .

Выпишем несколько полиномов:

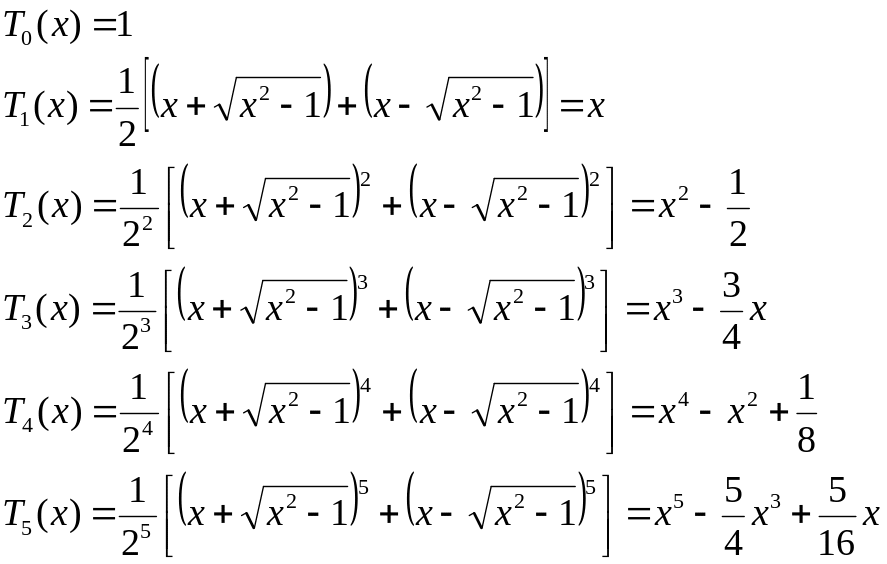
Полиномы Чебышёва образуют на отрезке ортогональную систему с весом

.

С использованием свойств косинуса полиномы можно определить и так:

, .

Рекомендуется самостоятельно проверить, что последнее соотношение даёт нужную последовательность.

Решив уравнение

,

можно найти корни -го полинома Чебышёва:

, , .

Эти корни и следует выбирать в качестве узлов интерполирования. Корни полиномов Чебышева расположены на интервале симметрично относительно нуля, но неравномерно – чем ближе к краям отрезка, тем корни расположены плотнее.

Так как , то и достигается в точках , . Очевидно, что

.

Известно, что для любого полинома степени с коэффициентом при старшей степени равным единице (каким я является ) верно неравенство

.

А поскольку для имеет место равенство, то полиномы Чебышёва являются полиномами, наименее уклоняющимися от нуля.

Таким образом, выбор в качестве узлов интерполирования корней полинома Чебышёва является наилучшим в смысле минимизации правой части оценки (см. формулу погрешности для полинома Лагранжа)

,

которая для полинома Чебышёва степени приобретает вид

,

.

В MathCad полиномы Чебышёва строятся так:

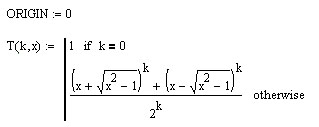
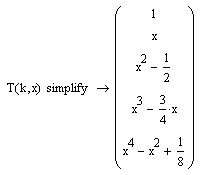
Графики полиномов до :

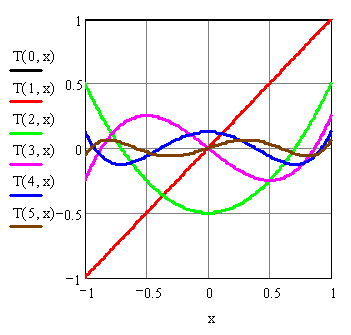
Приближающая для функция ищется в виде суммы полиномов Чебышёва:

,

, , .

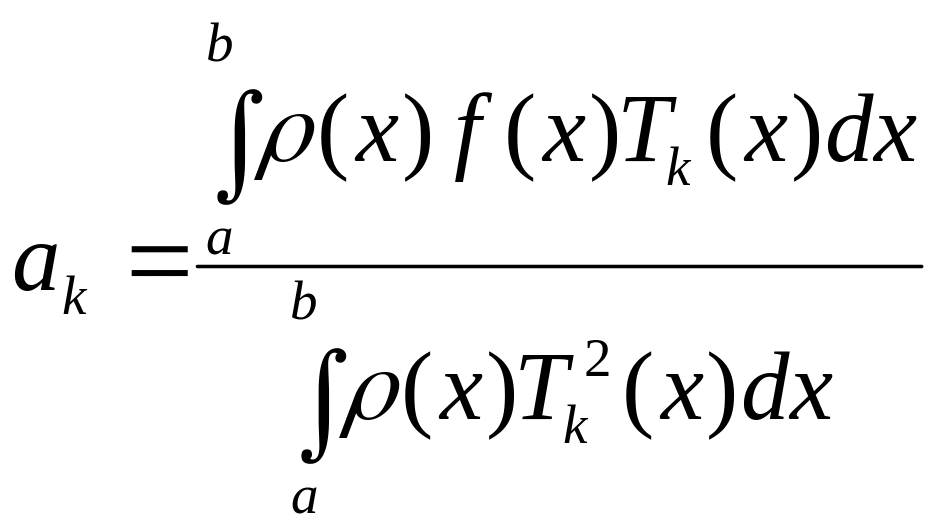Выше был указан выбор так называемых чебышёвских узлов

, ,

которые являются корнями -го полинома, причём .

Переход к общему случаю интерполирования функции на произвольном отрезке не представляет трудностей. Достаточно сделать линейную замену переменных, переводящую отрезок в отрезок . Такая замена производится по следующему правилу:

, , .

Тогда для произвольного отрезка чебышёвскими узлами будут узлы, вычисляемые по формуле:

, ,

где – степень полинома.

Оценка погрешности интерполирования для отрезка приобретает вид:

,

.

2.8.3. Интерполирование с использованием MathCad

Построим для функции на отрезке полином Чебышёва 4-й степени с весом . Он ищется в виде

, .

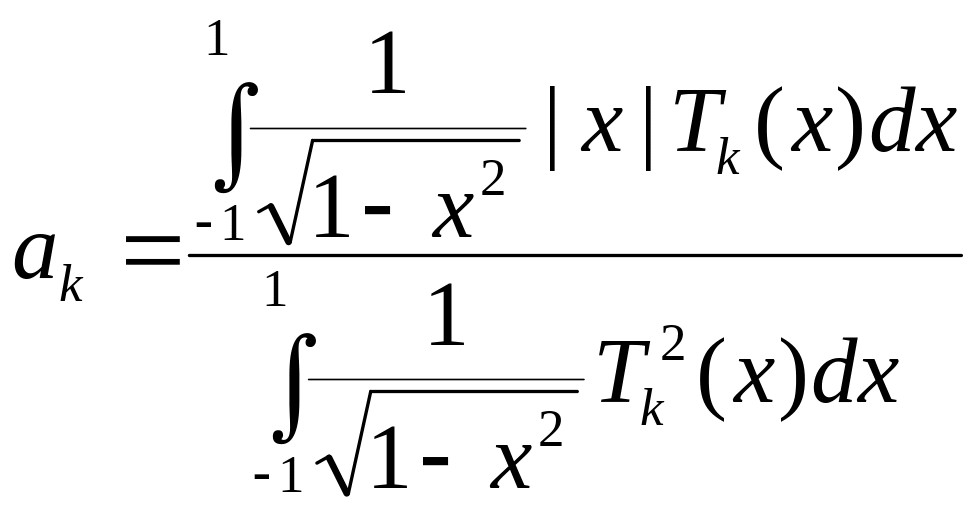Рабочий лист MathCad может быть следующим (с учётом фрагмента вычисления последовательности полиномов выше).

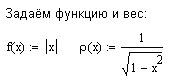
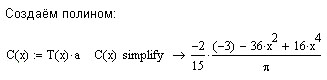
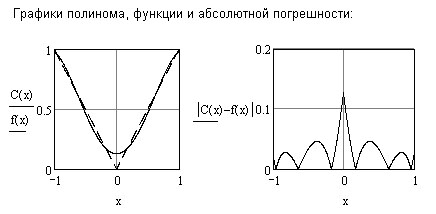
Упражнения

1. Для указанных ниже вариантов задания функций в среде MathCad провести вычисление значений полиномов Ньютона и Чебышёва в точках , , 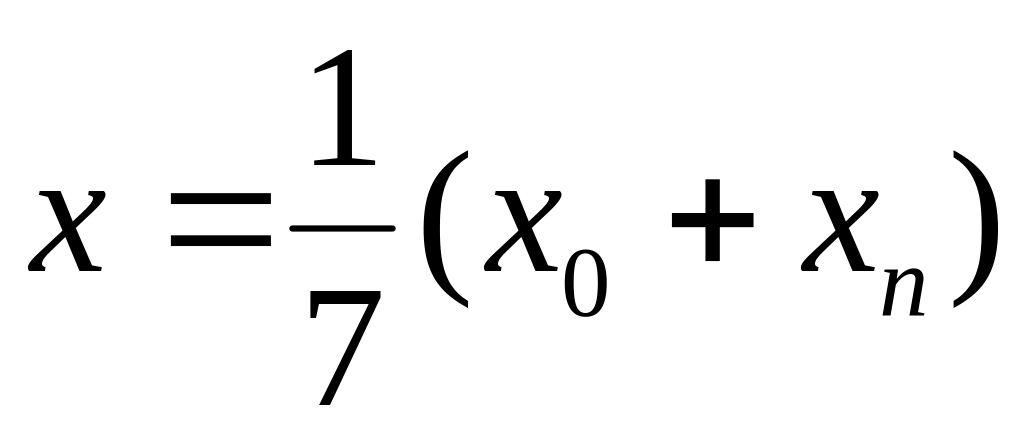, 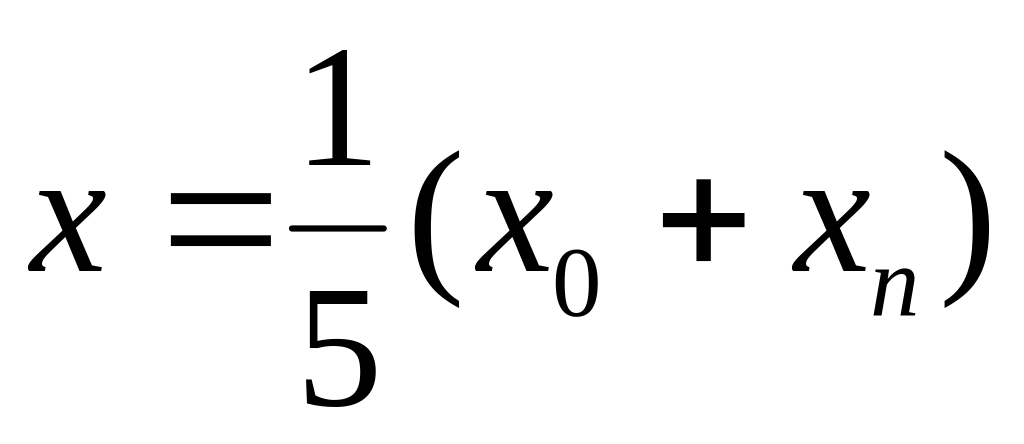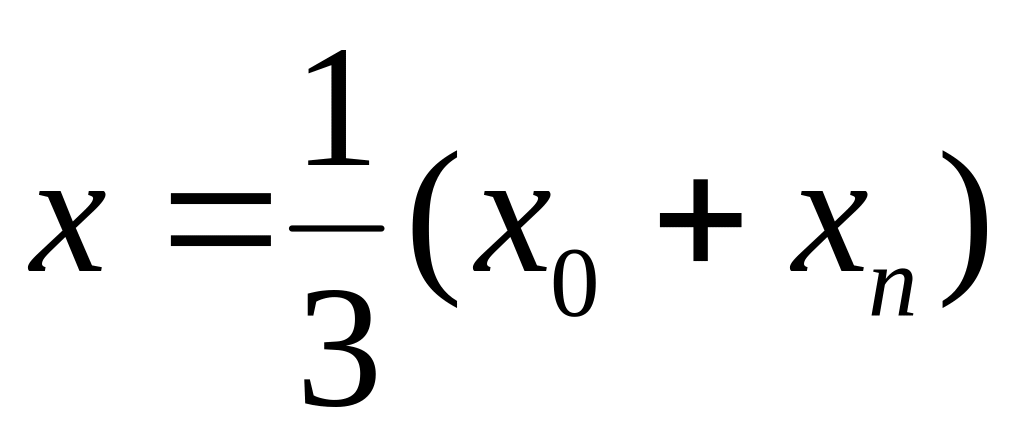с числом узлов 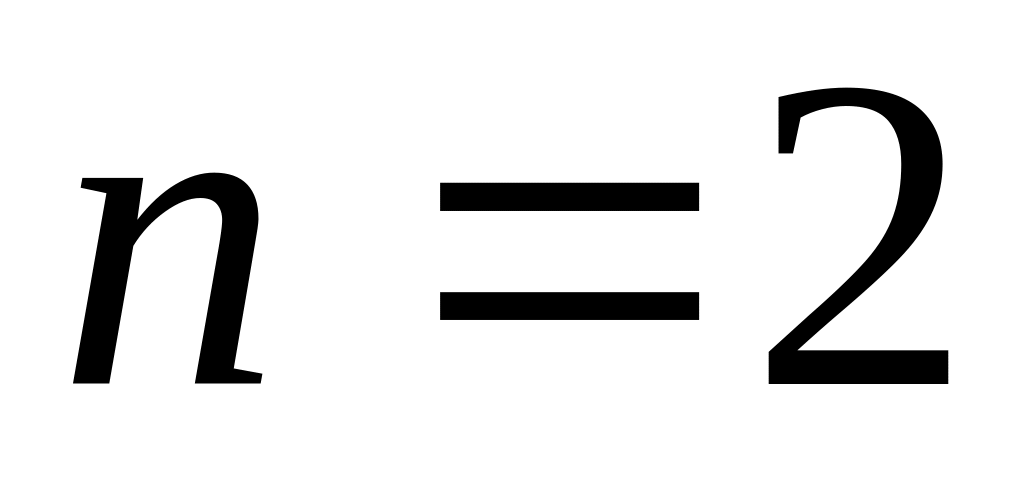, , 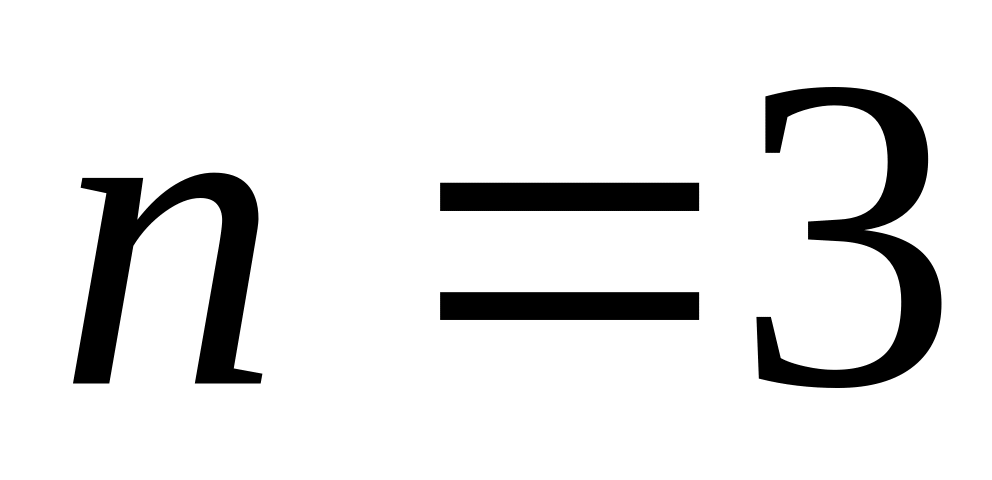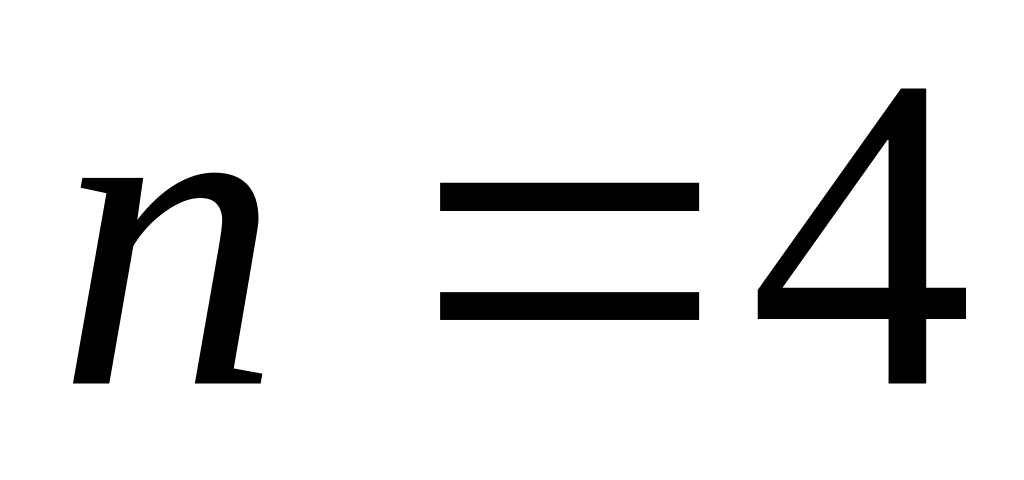( – также степень полинома Чебышёва). Вычислить погрешности интерполирования.

2. По результатам упражнения 1 для какой-либо фиксированной точки построить графики погрешностей 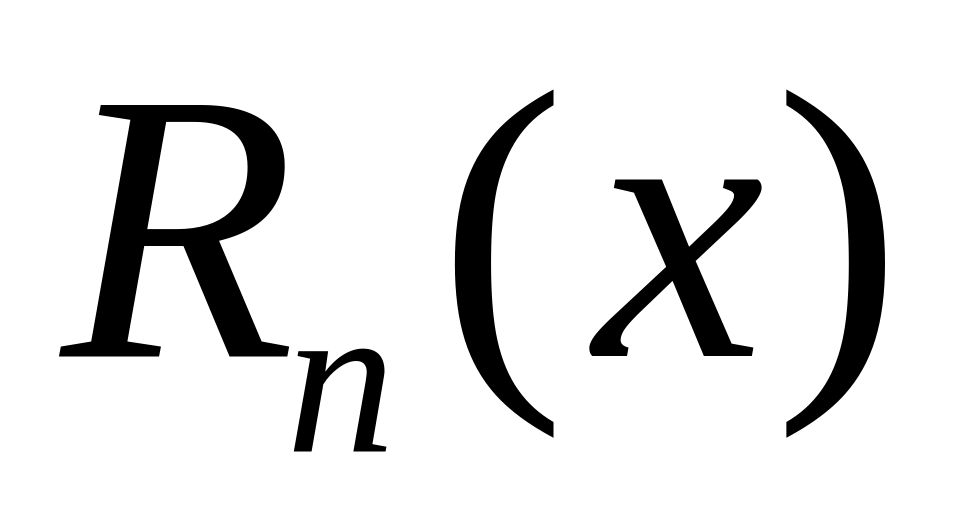полиномов Ньютона и Чебышёва в зависимости от числа узлов, т.е. графики функций .

3. Провести в MathCad сравнение интерполирования указанных ниже вариантов функций полиномом Лагранжа 3-й степени с равноотстоящими узлами и чебышёвскими узлами.

№				№
1		2	5	16		2	5
2		-9	9	17		-2	2
3		-2	2	18		-3	3
4		-1	5	19		2	5
5		-5	3	20		-3	3
6		1	3	21		-1	4
7		0	4	22		0	5
8		-5	5	23		-2	2
9		0	4	24		-2	3
10		-3	3	25		0	4
11		0	4	26		-3	3
12		0	8	27		-3	3
13		0	6	28		0	4
14		-3	2	29		-2	3
15		-4	-1	30		-2	2