2.6. Полином Ньютона для произвольных узлов

2.6.1. Вывод полинома

На практике встречаются таблицы с переменным шагом, то есть когда :

			...		...
			...		...

Такой характер имеют, как правило, эмпирические данные. Для таблиц с переменным шагом понятие конечных разностей обобщается. А именно, вводятся разделённые разности.

Разделённой разностью первого порядка называется отношение

, .

Например,

, .

Разделённой разностью второго порядка называется отношение

.

Например,

, .

Вообще, разделённые разности k-го порядка получаются из разностей -го порядка по формуле

, , .

Легко показать, что разделённые разности обладают свойством симметрии: .

Для получения полинома Ньютона рассмотрим разделённую разность

,

где подлежит определению. Отсюда .

Из разделённой разности второго порядка

имеем

или

.

Из разделённой разности третьего порядка имеем

или

.

Продолжая процесс дальше, получаем:

или

.

Выражение есть -я разделённая разность. Так как длина исходной таблицы значений функции равна , то . Следовательно, для неизвестной функции, заданной таблицей своих значений, имеет место приближённое равенство

.

При всех имеем равенства , следовательно, функция

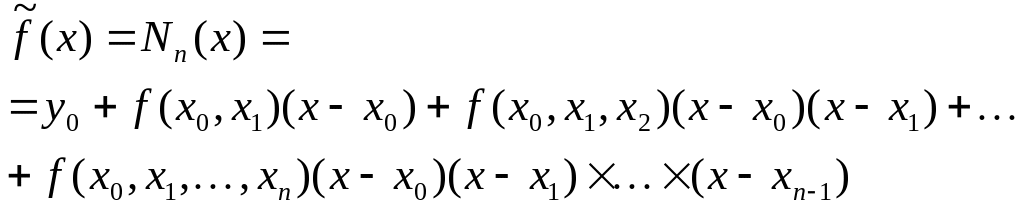
есть интерполяционный полином, который называется интерполяционным полиномом Ньютона для произвольных узлов. В силу свойства симметрии разделённых разностей имеем также:

Погрешность интерполяции в случае произвольных узлов совпадает с погрешностью интерполяции по Лагранжу, то есть

.

2.6.2. Пример ручных вычислений

Составим полином Ньютона по следующей таблице:

	0	1	2
	1	1.5	2.5
	1

Выпишем полином:

.

Вычислим разделённые разности:

,

.

Подставим данные и вычислим:

.

Полученный полином в точности совпадает с полиномом Лагранжа для произвольных узлов.

Упражнения

Получить полином Ньютона для произвольных узлов ручным способом:

1) с узлами , , , ; вычислить точное значение функции, значение полинома и абсолютную погрешность в точке .

2) с узлами , , ; вычислить точное значение функции, значение полинома и абсолютную погрешность в точке .

2.6.3. Интерполирование с использованием MathCad

Рабочий лист MathCad может иметь следующий вид.

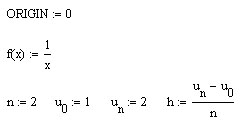
Вычисляем таблицу разделённых разностей:

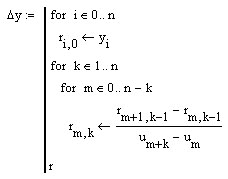
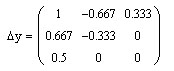
Полином имеет вид:

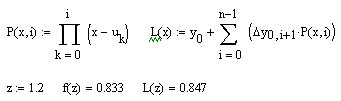
Упражнения

1. Получить в MathCad полиномы Ньютона для функций:

1. с узлами , , ; вычислить точное значение функции, значение полинома и абсолютную погрешность в точке , построить график погрешности;

2. с узлами, , , , ; вычислить точное значение функции, значение полинома и абсолютную погрешность в точках , , ; построить график погрешности.

2. Для функции на отрезке построить полиномы Ньютона для равноотстоящих узлов степени и получить график зависимости границы абсолютной погрешности от значения .