8.Идентификация систем управления. Идентификация в процессе управления. Классификация методов идентификации. Структура идентификации. Динамические методы идентификации

Задача идентификации формулируется следующим образом: по результатам наблюдений за входными и выходными переменными системы построить оптимальную в некотором смысле модель, т.е. дать формализованное представление этой системы. Задача идентификации базируется на современной теории управления.

Статистическая идентификация динамического объекта в частной области

X(t) Y(t)

W(j)

S_x() S_y()

Здесь W(j) - частотная характеристика динамического объекта; X(t) - случайный стационарный сигнал на входе объекта; Y(t) - случайный стационарный сигнал на выходе объекта; S_x(), S_y() - двухстороннее спектральные плотности сигналов X(t) и Y(t). Сигналы X(t), Y(t) имеют нулевое математическое ожидание.

Первый способ Известны вероятностные характеристики случайных процессов X(t), Y(t), например их спектральные плотности S_x(), S_y(). Требуется определить частотную характеристику W(j), передаточную функцию W(s) динамического объекта W(j)  W(-j) = .

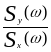Второй способ W(j) =

Третий способ (способ Райбмана) Пусть K_x(t) - корреляционная функция случайного процесса X(t) на входе объекта; K_yx(t) - взаимная корреляционная функция случайных процессов X(t) и Y(t). Представим K_x(t) и K_yx(t) в виде (5.11) . (5.12)

Тогда передаточная функция W(s) динамического объекта будет определятся соотношением W(s) = (5.13)

где

(5.14)

Здесь L{...}- преобразование Лапласа выражения в фигурных скобках.

Статистическая идентификация динамического объекта во временной области

В процессе нормального функционирования одномерного объекта синхронно (непрерывно или дискретно) измеряются входной x(t) и выходной y(t) сигналы. По результатам измерения необходимо определить хотя бы приближенное значение оператора, ставящего в однозначное соответствие входной и выходной сигналы, т.е. нужно получить математическую модель объекта. Основное уравнение статистической идентификации принимает вид

. (5.23)

При непараметрической идентификации динамических объектов решение уравнения Винера-Хопфа получают в виде последовательности значений ИПФ. Наиболее часто применяют численные методы решения уравнения (5.23) во временной и частотной областях.

Идентификация путем анализа импульсной реакции (весовой функции)

Рассмотрим систему, описываемую соотношением вида

(5.45) где u(t) - скалярный входной сигнал; y(t) - скалярный выходной сигнал; g₀(k) - истинная импульсная реакция или весовая функция, которая полностью определяет поведение системы; t = 0,1,2,... - дискретные моменты времени; v(t) - помеха в момент времени t.

Если к системе, описываемой соотношением (5.45), приложить импульсное воздействие

(5.46) то выходной сигнал y(t) будет равен

y(t) =α * g₀(t)+ v(t). (5.47)

Из (5.47) имеем

, (5.48) где - оценка весовой функции g₀(t); v(t)/α - ошибка определения g₀(t).Чтобы уменьшить v(t)/α, необходимо увеличить α.

При идентификации по импульсному воздействию часто возникают технические трудности, связанные с формированием и использованием импульсных входных сигналов. Этот метод нельзя применить к линеаризованным системам, так как амплитуда импульса по определению не может быть малой. Другими словами, при таком входном сигнале система может проявить нелинейные эффекты, нарушающие линеаризованное поведение, положенное в основу модели системы.

Этот метод предполагает идентификацию вне процесса управления.

Идентификация путем определения реакции на ступенчатое воздействие

Приложим к системе, описываемой соотношением (5.45), ступенчатое входное воздействие

(5.49) Тогда выходной сигнал y(t) будет равен

. (5.50) Из (5.50) имеем

. (5.51) Из (5.50), (5.51) получим

y(t) - y(t-1)= α * g₀(t)+ v(t) - v(t-1). (5.52)

Из (5.52) имеем

, (5.53) где - оценка весовой функции g₀(t); [v(t) - v(t-1)]/α - ошибка определения g₀(t). Если определение коэффициентов весовой функции действительно является целью, использование (5.53) может сопровождаться значительными ошибками в большинстве практических приложений.

Ступенчатый входной сигнал является наиболее простым для применения (он соответствует, например, открыванию или закрыванию входного клапана либо включению или выключению входного напряжения).

Классификация методов идентификации.

• Эмпирическая оценка передаточной функции ОУ(ТП)

• Частотный анализ корреляционным методом

• Регрессионная идентификация

• Статическая идентификация. Рекуррентные формулы

• Линейные регрессии и метод наименьших квадратов

• Метод инструментальных переменных

27