5.3. З'єднання ланок та алгоритмічні структурні схеми автоматичних систем

За допомогою типових динамічних ланок можна подавати не тільки окремі елементи системи, але й всю систему в цілому. Блок-схема системи, яка складається з окремих типових ланок, називається алгоритмічною структурною схемою і становить динамічну модель системи.

Основою алгоритмічної схеми АСР є функціональна блок-схема автоматичної системи, але в прямокутниках замість функціональної ознаки елементів записуються їхні передавальні функції. Елементи порівняння на алгоритмічній схемі зображуються так, як і на функціональній.

З алгоритмічною структурною схемою можна визначити передавальну функцію всієї системи та рівняння динаміки. Для цього треба знати правила перетворення структурних схем.

За умов послідовного з’єднання елементів:

W(р) - результуюча передавальна функція; W (р) W2(р).., W (р) - передавальні функції елементів; Д - знак добутку.

За умов паралельного з’єднання елементів:

За умови охоплення зворотним зв’язком:

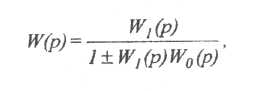
де W₁(р) і W₀(р) - відповідно передавальні функції з’єднання, що

охоплюється зворотним зв’язком, і кола зворотного зв’язку. Якщо зворотний зв’язок від’ємний, ставлять знак плюс, за умов додатного - мінус.

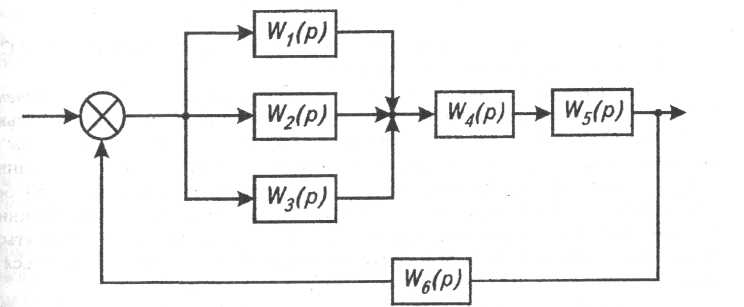
Рис. 5.6. Алгоритмічна структурна схема складної системи

Використовуючи наведені залежності можна АСР будь-якої складності звести до узагальненого елемента розімкненої системи W_р(р), охопленого

зовнішнім зворотним зв’язком W_зз(р), який з’єднує вихід системи зі входом.

Передавальна функція замкненої системи W_з(р) має вигляд:

W_з(р) = .

Як приклад, розглянемо алгоритмічну структурну схему складної системи (рис. 5.6) і визначимо загальну передавальну її функцію.

Визначаємо передавальну функцію паралельно з’єднаних елементів:

Потім визначимо передавальну функцію послідовно з'єднаних елементів

Загальна передавальна функція системи:

5.4. Перехідні процеси в замкненій аср

В замкненій АСР, з появою на вході об'єкта регулювання збурення, на його виході з'являється відхилення регульованої змінної та починає працювати автоматичний регулятор, з метою компенсації цього збурення. Таким чином, в АСР виникає перехідний процес (наприклад, рис. 5.7). Він може бути аперіодичним, коливальним затухаючим (збіжним), коливальним незатухаючим з постійною амплітудою та коливальним з наростаючою амплітудою (незбіжним).

Р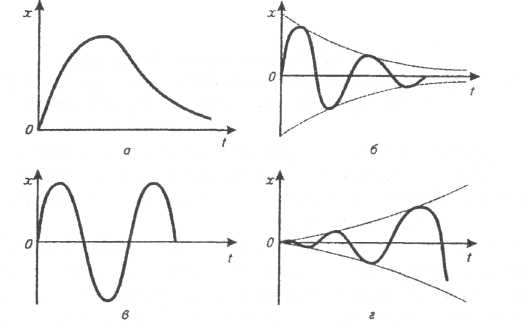 ис. 5.7. Графіки перехідних процесів:

а - аперіодичний; б - коливальний затухаючий; в – коливальний незатухаючий; г - коливальний наростаючий.

За умов аперіодичного перехідного процесу (рис. 5.7, а) регульована величина змінюється плавно і прямує до стану рівноваги, не переходячи через нього. Такі процеси можуть відзначатися великою тривалістю. За умов коливального затухаючого процесу (рис. 5.7, б) регульована зміна прямує до сталого значення, здійснюючи коливання з амплітудою, що поступово зменшується.

Якщо в перехідному процесі мають місце коливання з наростаючою амплітудою (рис. 5.7, г), то така система непрацездатна, тому що з часом відхилення регульованої змінної від заданого значення не зменшується, а зростає. Такі АСР називаються нестійкими. Якщо в системі виникає перехідний коливальний процес з постійною амплітудою коливань (рис. 5.7, в), то така АСР знаходиться на межі стійкості. Вона також непрацездатна. До стійких АСР відносяться системи, в яких протікають тільки аперіодичні або

коливальні затухаючі перехідні процеси.

Характер перехідного процесу залежить від зовнішніх збурень і від властивостей самої системи. Перехідний процес в системі можна показати двома складовими, одна з яких характеризує власні властивості системи, а друга - вплив збурюючих дій:

= + .

Система буде стійкою, якщо перехідна складова системи з часом

прямуватиме до нуля. Таким чином, висновок про стійкість лінійної системи можна зробити шляхом розв'язання рівняння динаміки системи, яке, в загальному випадку, описується звичайним диференціальним рівнянням -го

порядку з постійними коефіцієнтами:

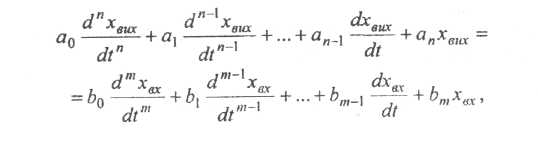
де х і х_вих – відповідно вхідна (управляюча чи збурююча) та вихідна регульована величини; а₀, а ... а_т ;b , b , ..., b - постійні коефіцієнти цього рівняння, що залежать від параметрів системи; та - порядок похідних, < . У операторній формі це рівняння має вигляд (12.6):

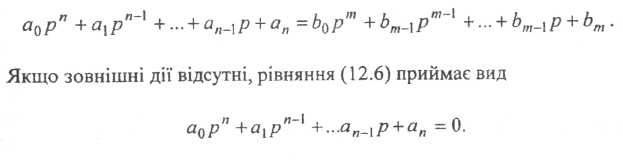(12.7)

Останнє рівняння (12.7) називають характеристичним.

Розв’язок такого рівняння становитиме суму експонент, степені яких є коренями характеристичного рівняння (12.7), помноженими на час:

= ,

де - постійні інтегрування; - корені рівняння.

Корені характеристичного рівняння можуть бути дійсними, уявними та

комплексними (мати дійсну та уявну частини). Математично доказано, що для забезпечення стійкості АСР дійсні корені, або їхня частина у комплексному корені, повинні бути від’ємними. При чисто дійсних коренях перехідні процеси в АСР аперіодичні і така АСР є стійкою. Якщо корені уявні, то АСР нестійка і в ній виникають гармонічні коливання постійної амплітуди. При комплексних коренях – в системі має місце коливальний (збіжний або ні) перехідний процес.

Значення цих коренів залежить від параметрів АСР, а також від налаштування регуляторів, що дозволяє цілеспрямовано змінювати

властивості АСР і робити їх стійкими.

Обчислення коренів характеристичного рівняння порівняно просте для АСР першого та другого порядків, а для вищих порядків приводить до громіздких розрахунків, тому для аналізу стійкості будь-якої системи, розроблені спеціальні критерії стійкості. Критерій стійкості – це непряма узагальнена оцінка, за допомогою якої просто виконується аналіз стійкості

АСР.

Перш ніж розглянути один із критеріїв, необхідно відмітити, що необхідною умовою стійкості системи будь-якого порядку є позитивність всіх коефіцієнтів характеристичного рівняння (12.6), тобто, а >0, a >0, … , a >0. Для систем першого та другого порядків ця необхідна умова є і

достатньою умовою стійкості.

Розглянемо один із найбільш широко вживаних - алгебраїчний критерій стійкості Гурвіца. Він дає змогу визначити стійкість системи, аналізуючи коефіцієнти характеристичного рівняння цієї системи. Для цього з коефіцієнтів характеристичного рівняння (12.6) складають головний визначник (матрицю) Гурвіца:

По головній діагоналі вписують коефіцієнти, починаючи від а до а . Колонки від елементів головної діагоналі вгору доповнюють коефіцієнтами з послідовно зростаючими індексами, униз — з індексами, що зменшуються. Всі вільні місця заповняють нулями.

У головному визначнику обводять, так звані, мінори і отримують

визначники нижчих порядків, починаючи із першого , що відповідає першому порядку і має тільки один елемент (верхній зліва) – коефіцієнт а , тобто, = а . Наступний мінор другого порядку об’єднує вже чотири коефіцієнти – два зліва у верхньому рядку (а та а ), та а і а - у другому рядку. Такими послідовними діями (по аналогії, наступний визначник об’єднує вже 9 коефіцієнтів) одержують (n-1) визначник. Система буде стійкою, якщо за а >0 всі визначники будуть додатні, тобто:

> 0; > 0; > 0;…; > 0 . (5.4.1)

Визначником, наприклад, другого порядку позначають вираз = а а -а а .

Умова(5.4.1) є необхідною і достатньою.

Розглянемо три приклади визначення стійкості для найпростіших систем:

умова стійкості: позитивність всіх коефіцієнтів характеристичного рівняння.