5.2. Основні ланки лінійних аср

1) Cтатична ланка першого порядку (або аперіодична).

Динамічна характеристика описується диференційним рівнянням першого

порядку у стандартній (канонічній) формі: , де Т – стала часу ланки, характеризує швидкість перебігу перехідних процесів, є мірою інерційності ; к - коефіцієнт підсилення ланки.

Застосовуємо операторну форму запису:

;

Перехідна характеристика (крива розгону):

Г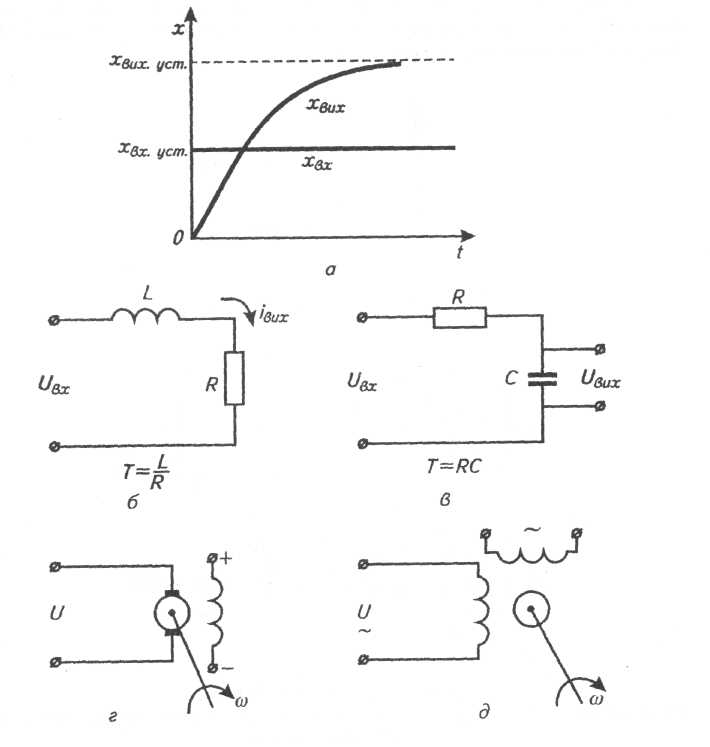 рафік кривої розгону – експонента. За умов стрибкоподібної зміни вхідної величини – вхідна змінюється повільно, відстаючи від вхідної, тому такі ланки називають інерційними (рис.5.1).

Рис.5.1. Крива розгону та приклади інерційних ланок :

а) крива розгону;

б-в) LR та RC – ланцюги (вхідна величина є напруга живлення, а вихідна –струм); електродвигуни постійного струму з незалежним збудженням;

г-д) вхідна величина - напруга живлення, а вихідна - швидкість обертання.

2) Статична ланка нульового порядку (підсилювальна ланка)

Рис.5.2. Безінерційні ланки: а) - крива розгону; - б) редуктор;

в) -подільник напруги;

г) - електронний підсилювач; д) - важільна передача.

Це безінерційні ланки з рівнянням динаміки: Х_вих = к Х_вх ,

де к – коефіцієнт підсилювання ланки.

Передавальна функція: W(р) = к. З подачею на вхід стрибко-подібного сигналу вихідна величина без запізнення повторює зміну вхідної.

3)Астатична (інтегрувальна) ланка 1-го порядку

Диференційне рівняння динаміки: або

і відповідно: ; .

Перехідною характеристикою інтегруючої ланки є пряма, що проходить через початок координат під кутом α до осі часу tgα = k (рис.5.3 , а).

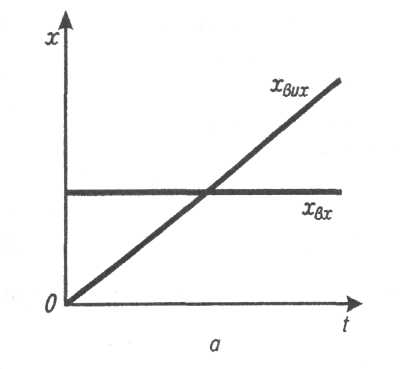
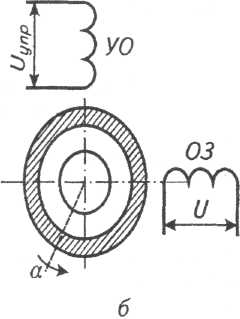
Рис.5.3. Інтегруючі ланки: а - крива розгону; б – електродвигун.

Приклад астатичної – електродвигун, коли вихідним сигналом є напруга управління, а вихідним – кут α повороту ротора.

4) Диференціювальна ланка

Диференціювальною називається ланка – в якій вихідна величина

пропорційна швидкості зміни вхідної Х_вих(t) = k (Х_вх/dt )(це ідеальна ланка). Відповідно: Х_вих = k p Х_вх; W(p) = k р.

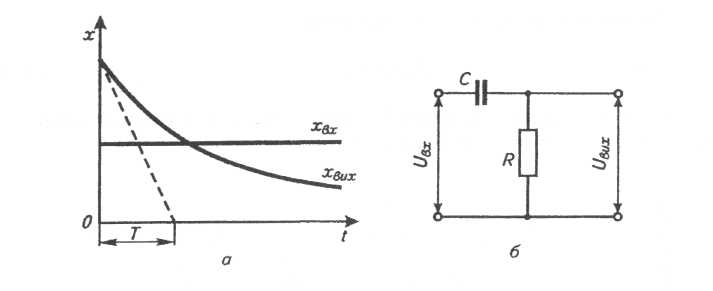
Рис. 5.4. Реальна диференціювальна ланка: а - крива розгону; б – RC-контур.

Регульована змінна її прямує до ∞ (при Δt>0). Такий перехідний процес

неможливий, тому на практиці використовуються реальні диференціювальні ланки (рис. 5.4).

5) Коливальна ланка. Динамічні властивості цієї ланки (рис. 5.5) описуються рівнянням:

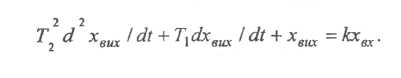
де Т₁, Т₂ - сталі часу; k - коефіцієнт підсилювання.

У операторній формі рівняння має вигляд:

Передаточна функція:

До коливальної ланки відносяться пристрої, в яких вихідна величина після

подавання на вхід стрибкоподібного збурення прямує до усталеного

значення, здійснюючи коливання. Ця ланка складається якби з двох елементів, що можуть акумулювати енергію або речовину та обмінюватись нею між собою.

Рис. 5.5 Коливальна ланка: а) – крива розгону за умови Т₁<2Т₂; б) –сполучені посудини; в) – вантаж масою m; підвішний на пружині; г) – крива розгону за умови Т₁>2Т₂; д) – контур RLC.

Якщо Т₁<2Т₂, перехідний процес буде мати вигляд затухаючих коливань. За умов Т₁>2Т₂перехідний процес не буде коливальним, в цьому випадку ланка буде називатися аперіодичною другого порядку (рис. 5.5, а, г). Якщо Т₁=0, то ланка називається консервативною і перехідний процес являє собою гармонічні коливання з постійною амплітудою. Прикладами коливальних ланок можуть бути (рис. 5.5, б, в, д); сполучені судини; вантаж з масою m, підвішений на пружині; електричний контур RL або RС.

6) Ланка чистого запізнювання. Вихідна величина ланки повторює зміну вхідної величини, але з деяким постійним запізнюванням (рис. 5.5). Рівняння

ланки та передаточна функція мають вигляд:

Х_вих (t) = Х_вх(t - τ),

де t та (t—τ) - не множники, а символи; τ - чисте запізнювання.

Рис. 5.5. Ланка чистого запізнювання

Прикладами ланок чистого запізнювання можуть бути трубопровід,

транспортер та ін.