4.4. Дискретні двопозиційні регулятори

Серед регуляторів дискретної дії найбільш поширені двопозиційні

(релейні) та імпульсні регулятори.

У двопозиційних регуляторах регулюючий орган може займати одне із двох положень «Відкрито-Закрито». При регулюванні температури в теплообміннику двопозиційний регулятор переключає РО, коли температура досягне заданого максимального або мінімального значення. Характеристика двопозиційного регулятора має вигляд, приведений на рис. 4.7.

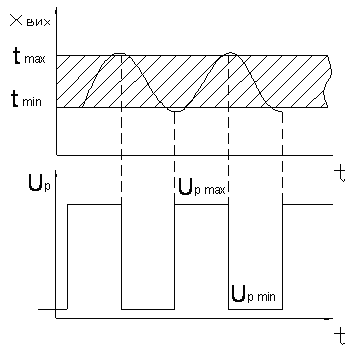
Рис. 4.7. Характеристика двопозиційного регулятора.

Видно, що процес має автоколивальний характер. Різниця між максимальним і мінімальним значенням Х_вих регульованої змінної називається зоною нечутливості позиційного регулятора, бо коли значення Х_вих знаходиться всередині зони, регулятор не реагує на її зміну. Переключення РО відбувається лише тоді, коли регульована змінна Х_вих досягне однієї із границь нечутливості. Частота переключень залежить від сталої часу Т об’єкта регулювання і чим вона менша, тим частіше відбувається переключення і тим швидше система виробить свій ресурс. Тому двопозиційні регулятори використовуються для достатньо інерційних об’єктів і технологічні вимоги до яких допускають досить значні коливання регульованої змінної.

4.5. Динамічні характеристики релейно-імпульсного регулятора

Динамічні властивості релейно-імпульсного регулятора визначаються двома вузлами: регулюючим блоком (РБ) та виконавчим механізмом (ВМ) з постійною швидкістю обертання (рис. 4.8). Регулятор працює, як правило, на ВМ, що виконаний на базі асинхронного електродвигуна з редуктором, і

вмикається в роботу за допомогою пускового пристрою (ПП).

Рис. 4.8. Структурна схема релейно-імпульсного регулятора

Особливість ВМ постійної швидкості обертання в тому, що він

розрахований на визначену напругу живлення і не може керуватись за рахунок її зміни. При появі досить потужного регулюючого сигналу U_р(t) пусковий пристрій подає живлення на електродвигун ВМ. Останній приводить до переміщення РО з постійною швидкістю , яка не залежить від значення регулюючої дії U_р(t). Канал U_р(t)→ Х_вих(t) - є нелінійною ланкою.

Вихідна регулююча дія на об’єкт регулювання Х_ро(t) такого ВМ в відповідності із необхідним законом регулювання (наприклад, ПІ), отримується за допомогою імпульсного способу керування ВМ. Суть його роботи характеризується чередуванням короткочасних вмикань (імпульсів довжиною Δt_вмк) та відключень (Δt_відкл). При кожному ввімкненні ВМ РО переміщується на величину Δt_ро=V*Δt_вмк, а вперіод пауз положення РО не змінюється.

.

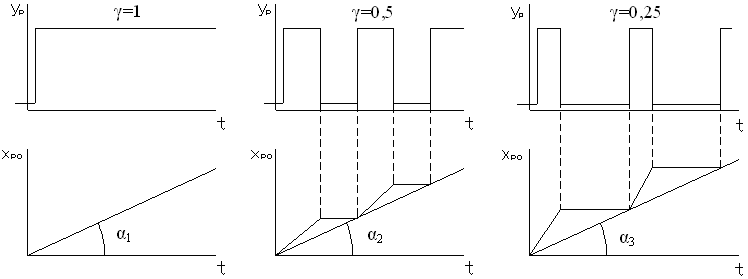
Рис. 4.9. Графіки роботи імпульсного регулятора при різних скважностях.

Як правило, велика постійна часу самого технологічного процесу та його інерційність, призводить до фільтруючих властивостей і таке дискретне переміщення РО сприймається об’єктом управління, як плавне, з деякою

середньою швидкістю Х_ро яка називається швидкістю регулювання.

Середнє значення швидкості регулювання Х_ро характеризується відношенням переміщення ΔХ_ро РО в плинний час одного імпульсу, яке

дорівнює ΔХ_ро=V₀۰ Δt_вмк , до періоду надходження імпульсів (Δt_вмк+Δt_відкл):

,

де γ - скважність керуючих імпульсів.

При імпульсному регулюванні середня швидкість регулювання пропорційна швидкості керуючих імпульсів U_р. Змінюючи скважність γ(t) (рис. 4.9) керуючих імпульсів U_р в залежності від сигналу Δх(t) можна отримати необхідну керуючу дію Х_ро(t) на регулюючий орган.

РОЗДІЛ 5

ДИНАМІЧНІ ВЛАСТИВОСТІ АСР ТА ЇЇ СКЛАДОВИХ

5.1. ПОДАННЯ ЕЛЕМЕНТІВ АСР ЛАНКАМИ.

ПЕРЕДАТОЧНА ФУНКЦІЯ АСР. ПЕРЕТВОРЕННЯ ЛАПЛАСА

Динамічні властивості АСР в цілому визначаються динамічними властивостями всіх її складових, тобто, автоматичного регулятора (АР) та самого об’єкта. Для дослідження динамічних властивостей АСР використовують різні математичні моделі (ММ) у вигляді динамічних характеристик і зв’язків між ними. Один із ефективних прийомів одержання і представлення ММ АСР є використовування типових елементарних динамічних ланок. Ідея методу полягає в тому, що при створенні ММ використовуються елементарні ланки з наперед заданими (відомими) властивостями. При цьому система АСР розділяється на окремі елементи, що відрізняються один від одного не за функціональною ознакою, а за динамічними властивостями, і являє собою сукупність цих ланок та певних зв’язків між ними.

Алгоритмічною ланкою автоматичної системи називається найпростіша складова частина, яка відображає її динамічну властивість і яка має один вхід і

один вихід.

Незважаючи на велику різноманітність систем автоматичного регулювання

та елементів, що входять в них, існує всього декілька динамічних ланок, які використовуються для опису будь якої системи чи АСР.

Ланки АСР є детектуючими, тобто, сигнал може проходити через ланку тільки в одному напрямку – від входу до виходу. Це дозволяє розглядати кожну ланку окремо від усієї системи.

Не завжди один конструктивний елемент замінюється однією ланкою. Інколи елемент може бути поданий комбінацією із кількох ланок. Можна отримувати ММ АСР різного ступеня деталізації.

До динамічних характеристик ланок відносяться: рівняння динаміки, перехідні характеристики та передаточні функції.

Під передаточною функцією (зображається W(р) розуміють відношення вихідної величини ланки до вхідної. Передаточну функцію одержують із диференційного рівняння ланки, при цьому використовують операторну форму запису, яка дає можливість знак диференціювання d/dt замінити оператором Р. Такий перехід від функції часу x(t) до її зображення Х(р) називається прямим перетворенням Лапласа і визначається формулою:

Це співвідношення ставить функцію х(t) дійсної змінної у відповідності

функції Х(р) комплексної змінної, яка = . При цьому х(t) називається оригіналом, а Х(р) – відображенням по Лапласу. Те, що х(t) має своїм відображенням Х(р) записується ще так:

Х(р) = L{ х(t) }, тобто, х(t) присвоїти Х(р), де L – прямий оператор Лапласа.

Зворотна операція переходу від операторного зображення Х(р) до функції х(t) (оригіналу) зветься зворотнім перетворенням Лапласа. В більшості практичних задач здійснюється за допомогою таблиць, які приведені в довідниках по операційному обчисленню. Для визначення оригіналу по його відображенню, тобто, Х(р) присвоїти х(t), застосовують формулу:

= , де - обернений оператор Лапласа.

Широке застосування перетворення Лапласа в теорії автоматичного управління (ТАУ) обумовлене тим, що за його допомогою визначається передавальна функція, яка є компетентною формою опису динамічних властивостей елементів і систем. У результаті такого перетворення можна розв’язати диференційне рівняння алгебраїчно, що спрощує рішення диференційних рівнянь, в тому числі і вищих порядків,

наприклад, ; ; .

Передаточна функція ланки W(p) визначається як відношення операторного зображення вихідної величини Х_вих(р) до операторного значення вхідної величини Х_вх(р): W(p) = Х_вих(р)/ Х_вх(р).

Фізична суть поняття передаточної функції полягає у тому, що вона однозначно показує , як передається вхідний сигнал на вихід елемента чи системи. Тобто, при заданій W(p) і певному вхідному сигналі Х_вх(р) завжди однозначно визначається вихідний сигнал Х_вих(р):

Х_вих(р) = W(p) * Х_вх(р).

Перехідні характеристики ланок – є часовими характеристиками і показують як

протікають в них перехідні процеси, тобто, яка є реакція ланки на вхідні сигнали х(t) і зображується як траєкторія зміни Х_вих(t) у часі.

Для порівняння характеристик різних ланок використовуються типові вихідні сигнали – стрибкоподібний або імпульсний. В цьому випадку траєкторія зміни Х_вих(t) називається кривою розгону.