Лабораторна робота № 1

ВИМІРЮВАННЯ ТЕПЛОЄМНОСТІ ПОВІТРЯ

1. Ціль роботи

Ціль роботи – поглибити знання з розділу «Властивості ідеальних газів. Теплоємність газів»; ознайомитись з основними принципами проведення калориметричного досліду.

2. Завдання

1. Виміряти середню об'ємну ізобарну теплоємність повітря методом проточного калориметру.

2. За даними вимірювань розрахувати масову ізобарну і масову ізохорну теплоємності повітря.

3. Оцінити точність одержаних експериментальних даних і порівняти їх з наведеними в літературі.

3. Загальні відомості

Теплоємністю називається фізична величина, яка чисельно дорівнює кількості теплоти, необхідної для зміни температури тіла на один градус. Якщо кількість теплоти віднести до одиниці кількості речовини, теплоємність буде питомою:

масовою - с , кДж/кг·К;

молярною - с_µ, кДж/кмоль·К;

об'ємною - с´, кДж/м³_ну·К;

де м³_ну – кубічний метр за нормальних умов, Р_ну=760мм рт. ст; Т_ну=273,15 К.

Між питомими теплоємностями існують такі співвідношення:

; ; , (1.1)

де µ - молярна маса газу, кг/кмоль;

v_µ- молярний об'єм газу, м³/кмоль;

ρ - густина газу, кг/м³.

В залежності від процесу, в якому здійснюється підведення або відведення теплоти, теплоємність може змінити своє значення від 0 (в адіабатному процесі) до ±∞ (в ізотермічному процесі). Велике практичне значення мають теплоємності в ізобарному с_р і в ізохорному с_v процесах.

Для ідеального газу справедливо співвідношення, так зване рівняння Майєра:

C_p – C_v = R (1.2)

де R – питома газова стала, кДж/(кг·К).

В термодинамічних розрахунках часто використовується відношення с_р і с_v, або показник адіабати - k:

(1.3)

У відповідності з молекулярно-кінетичною теорією теплоємність ідеальних газів не залежить від температури; залежність теплоємності реальних газів від температури встановлюють експериментально. Теоретичні значення теплоємності газів в залежності від температури вираховуються на основі спектроскопічних даних з використанням квантової статистики і наводяться у відповідних таблицях.

Розрізнюють дійсну теплоємність при даній температурі , тоді 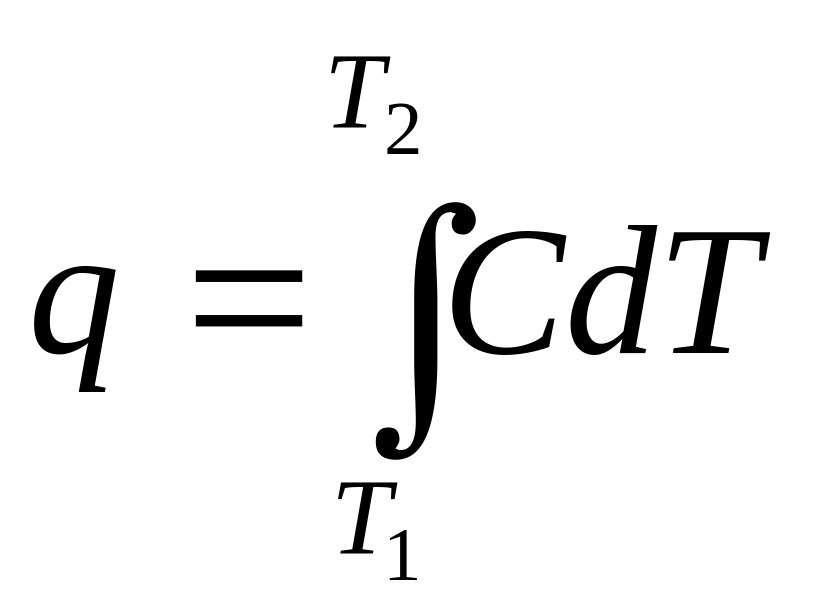,(де Т₁,Т₂ – границі інтервалу температур) і середню теплоємність в інтервалі температур ΔТ=Т₂-Т₁ , звідки .

4. Опис методики експерименту

Одним з найбільш поширених методів вимірювання теплоємності газів є метод проточного калориметру. До потоку газу, що протікає крізь калориметр, підводять деяку кількість теплоти Q, яка викликає зміну температури від Т₁ до Т₂. Після встановлення стаціонарного режиму температура газу на вході в калориметр і виході з нього не змінюється і кількість теплоти залишається сталою. На рис. 1.1 показана спрощена схема проточного калориметра, де газ рухається зліва направо, нагрівання газу відбувається між перерізами 1 і 2.

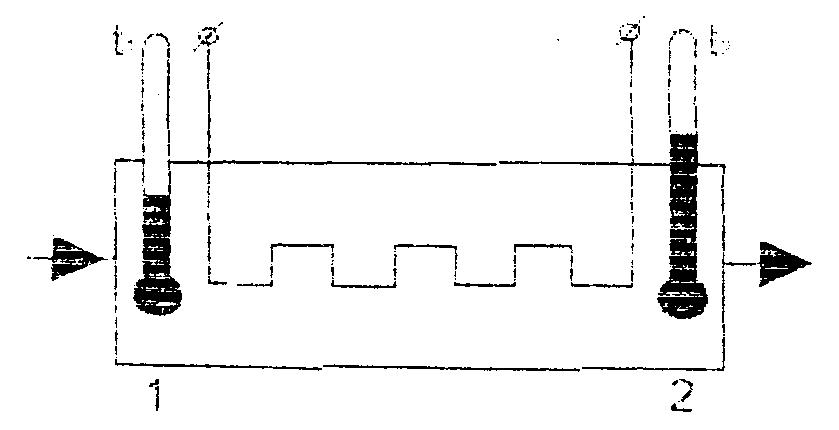
Рис. 1.1. Схема проточного калориметра.

Для перерізів 1 і 2 калориметра запишемо повне рівняння першого закону термодинаміки для 1 кг потоку (потік стаціонарний).

, (1.4)

де q_ел - кількість теплоти, підведеної в електричному нагрівачі до 1 кг газу, який проходить крізь калориметр; h₂, h₁ – питомі ентальпії газу в перерізі відповідно 1 і 2; w₁, w₂ – швидкості газу в перерізі відповідно 1 і 2; l_техн – технічна робота; q_вт – теплові втрати в навколишнє середовище в розрахунку на 1 кг газу, g – прискорення вільного падіння, b₁,b₂ – відстані по вертикалі від довільної горизонтальної площини до осі потоку в перерізах 1 та 2, (всі доданки рівняння (1.4) мають розмірність Дж/кг = м²/с²).

Фізичний зміст рівняння (1.4) полягає в тому, що підведена до потоку енергія q_ел може бути витрачена на:

1. збільшення питомої ентальпії потоку на Δh = h₂ - h₁ (для газу це пов’язано як зі збільшенням внутрішньої енергії u внаслідок збільшення темпе-ратури, так і внаслідок збільшення добутка p₂v₂ > p₁v_1, оскільки t₂>t₁ ). Обидві складові ентальпії h=u+pv відображають ту частину потенційної енергії потоку, яка залежить від температури та тиску;.

2. збільшення кінетичної енергії потоку ( для газового потоку при сталому перерізі S₁=S₂ (S-площа перерізу) збільшення швидкості w₂>w₁ відбувається внаслідок зменшення густини газу при підвищенні температури при практично незмінному тиску ρ₂ > ρ₁ , це випливає з рівняння нерозривності потоку (незмінності масових витрат):

ρ₁w₁S₁ = ρ₂w₂S₂ .

3. виконання технічної роботи (якщо в каналі розташувати, наприклад, пропелер ),

4. збільшення потенційної енергії положення (відносно поверхні Землі), якщо b₁<b₂ ,

5. втрати теплоти в оточуюче середовище q_вт.

Так як 1) швидкості газу w₁, w₂ відрізняються одна від одної незначно, 2) технічна робота не виробляється; 3) висоти b₁ і b₂ відрізняються одна від одної також незначно, то відповідні члени із рівняння (1.4) випадають і залишаються такі:

q_ел - q_вт = h₂ – h₁ (1.5)

В загальному випадку ентальпія газу залежить від температури і тиску і диференціал ентальпії має вигляд:

(1.6)

Так як повітря при атмосферному тиску за своїми властивостями дуже близьке до ідеального тазу, член =0. Тоді для інтервалу температур t₁-t₂:

. (1.7)

З врахуванням (1.5) маємо:

. (1.8)

. (1.9)

В (1.8) величини q_ел і q_тв визначаються на 1 кг газу, а в експерименті за 1с проходить т кг повітря, тому розрахункову формулу можна записати у вигляді:

, (1.10)

де –Q_ел, – надходження електричної енергії за 1 с (електрична потужність, Вт),

Q_вт – втрати енергії за 1 с, Вт.