4.1.2 Определение расхода жидкости q

Расходом потока называется количество жидкости, протекающее через некоторое поперечное сечение потока в единицу времени. Это сечение должно быть сделано так, чтобы обязательно пересекало каждую элементарную струйку и только один раз. Обычно за поверхность сечение принимают живое сечение потока. Для аналитического вычисления расхода необходимо знать закон распределения скоростей по сечению потока.

Расход потока выражается или в весовых единицах, например в кГ/сек, или в массовых единицах, например в кГ·сек/м, или в объемных например, в м³/сек. В первом случае расход будет называться весовым (G), во втором - массовым (М) и в третьем- объемным (Q).

Запишем уравнение неразрывности для сечения 1-1 и 2-2:

Q1=Q2, следовательно v1*S1=v2*S 2 (1)

Отсюда, v2=v1* S1/S2 (2)

Запишем уравнение Бернулли для двух сечений 1-1 и 2-2:

. (3)

где , - расстояния от сечений А-А и В-В соответственно до некоторой произвольно выбранной горизонтальной плоскости (м);

, - давления в сечениях А-А и В-В соответственно (Па);

- плотность циркулирующей жидкости (кг/м³);

g - ускорение свободного падения (м²/с);

V₁ ,V₂ - скорость течения жидкости в сечение А-А и В-В соответственно (м/с);

, - коэффициенты Кориолиса, которые учитывают неравномерность распределения скоростей в сечениях А-А и В-В соответственно;

- потери напора на участках между выбранными сечениями.

Выберем ось трубопровода за начало отсчета, тогда z1=z2=0, т.к. трубопровод горизонтален. Предположим, что по трубопроводу течет идеальная жидкость. Это не позволяет учитывать потери напора hA-B=0.

= =1

Запишем уравнение Бернулли (3) с учетом всех утверждений:

(V1)²/2g-(V2)²/2g=(P2-P1)/ρ1g (4)

Подставив в это уравнение (2) получаем:

(V1)²/2g- (V1)²(S1/S2)² /2g=(P2-P1)/ρ1g =>

=>(V1)²(1-(S1/S2)²)=2(P2-P1)/ρ1 => v1=2(P2-P1)/ρ1(1-(S1/S2)²) (5)

Из рисунка видно, что

(P2-P1)/ρ1g=h,

Где h=hвен((ρрт/ρ1)-1) (6)

Теоретический расход будет меньше, т.к существует потери напора. Учтем это с помощью поправочного коэффициента, который называется коэффициентом расхода μ.

Q=μвенS1v1, где S1=Sвен (7)

Подставив в (7) уравнение (5) с учетом (6):

Q=(μвен*π d²вен/4)*((2g hвен((ρрт/ρ1)-1))/((1-(dвен/d2)⁴))^1/2

Q=0.97*(3.14*(0.05)² /4)*(2*9.8*215*((13600/1000)-1)/(1-(0.05/0.081)⁴))^1/2=

=0,014 м³/с

Значение Q, м3/с

Q=0,014

4.1.3 Определение потерь напора

Определение величины потерь напора при движении реальных жидкостей является одной из основных задач практической гидравлики. При движении реальной жидкости энергия движения (напор) жидкости будет убывать по направлению движения. Причиной этого являются затраты энергии на преодоление сопротивлений движению, обусловленные внутренним трением в вязкой жидкости. В гидравлике различают два основных вида сопротивлений:

1. Потери напора по длине, т.е. сопротивления, проявляющиеся по всей длине потока, обусловленные силами трения частиц жидкости друг о друга и о стенки, ограничивающие поток. Это линейные потери. Они определяются по формуле Дарси-Вейсбаха:

(1)

где – длина трубы (или участка трубы) на котором определяются потери напора»

– диаметр трубы;

– средняя скорость в трубе;

λ = λ (Re, ∆/d ) – коэффициент гидравлического сопротивления трения.

Коэффициент гидравлического сопротивления трения (λ) зависит от двух безразмерных параметров Rе – числа Рейнольдса и ∆/d – относительной шероховатости трубы. Число Рейнольдса определяется по формуле:

(2)

где μ – динамическая вязкость жидкости (Па·с);

– кинематическая вязкость жидкости (м²/с).

Для определения коэффициента гидравлического сопротивления трения существуют много различных формул. Удобно пользоваться следующими формулами. Для ламинарного режима движения:

λ =64/Rе, Rе < 2000÷2320.

Для турбулентного режима движения (формула Альтшуля):

λ=0,11(68/Rе+ ∆/d) , Rе >2000÷2320

2. Местные потери напора, так называемые местные сопротивления, обусловленные различного рода препятствиями, устанавливаемыми в потоке (задвижка, кран, колено), приводящими к изменениям в величине или направлении скорости течения жидкости. Потери напора на местных сопротивлениях определяются по формуле

(м) (3)

где – средняя скорость движения жидкости;

– коэффициент местного сопротивления.

Потеря напора на местном сопротивлении может определяться как по скорости до местного сопротивления, так и по скорости после местного сопротивления. Так как скорости по величине могут быть разными, то в этих случаях для одного и того же местного сопротивления будут разные значения . Принято определять потери напора по скорости после местного сопротивления. Исключение составляет расширение трубопровода (выход потока из трубы в бак), где потери определяются по скорости до местного сопротивления.

Для определения потерь напора по данной курсовой работе будем учитывать как потери напора по длине трубопровода, так и местные сопротивления.

hА-В = hд + hм (м) (4)

где hд – потери напора по длине трубопровода (м);

hм – потери напора от местных сопротивлений.

а) Вначале определим hм – потери напора от местных сопротивлений. Для этого сложим все местные сопротивления на рассматриваемом участке:

hм = hкор+ hкол +hзад

где hкор – потери напора на коробке всасывающей линии;

hкол – потери напора на колене всасывающей линии;

hзад – потери напора на задвижке всасывающей линии.

Используя формулу (3) получим:

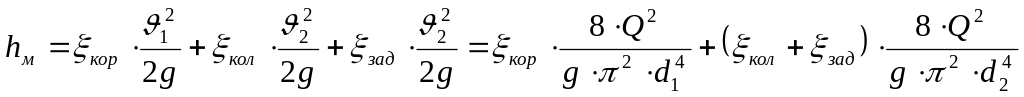(5)

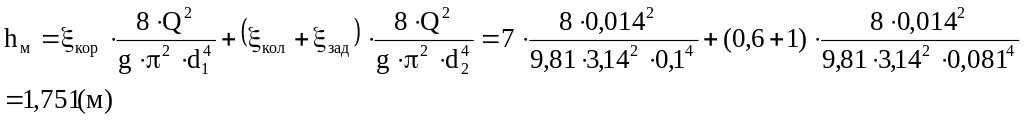
б) Теперь рассчитаем hд – потери напора по длине трубопровода. Они определяются как сумма потерь напора на участке трубопровода и потерь напора на участке трубопровода :

hд =hд1 +hд2 (м) (6)

(м) (м)

где λ1 и λ2 – коэффициенты гидравлического сопротивления 1 и 2 участков.

Для определения λ1 и λ2 необходимо определить режим течения жидкости на соответствующих участках трубопровода. Для этого определим числа Рейнольдса для этих участков по формуле (2):

= =

где ν – кинематическая вязкость циркуляционной жидкости.

=

=

По полученным результатам вычисления чисел Rе определяем режим течения – турбулентный или ламинарный.

Затем определим тип трубопровода (шероховатый или гладкий) на участках трубопровода и . Для этого находим значения величин обратной относительной шероховатости для обоих рассматриваемых участков по данным значениям d и ∆:

и

Оба участка принадлежат зоне шероховатых труб, если их числа Rе принадлежат промежуткам:

6667 < 178343,949 ≤ 333350

5400< 70175,4386 ≤ 270000

Оба участка принадлежат зоне шероховатых труб, т.к выполняются условия. Для определения λ₁ и λ₂ воспользуемся формулой Альтшуля:

λ₁=0,11(68/Rе₁+∆/d₁) =0,11(68/178343,949+0,00014/0,1)^0,25=0,0229

λ₂=0,11(68/Rе₂+∆/d₂) =0,11(68/70175,4386+0,00014/0,081)^0,25=0,0253

Теперь, когда известны все величины, можно найти суммарные потери напора на участках и (по формуле (6)):

h_д= h_д1+ h_д2

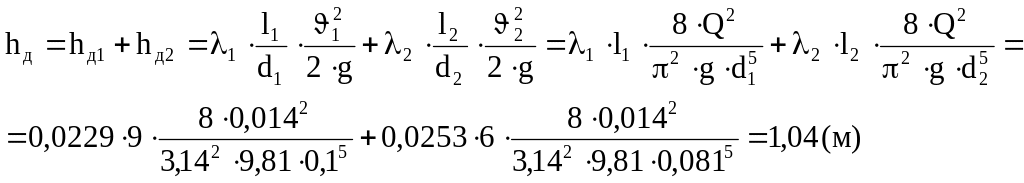
hА-В = hд + hм=1,04+1,751=2,791 (м)

Подставим полученные значения в формулу (4) определим необходимую величину hА-В .

Значение hА-В, м

2,791

Заканчивая расчетную часть по первому пункту задания, т.е. нахождение геометрической высоты всасывания насоса H₂, воспользуемся формулой (4) из пункта 4.1.1.:

(м)

Значение H2, м

3,453