Лабораторна робота №11 Експериментальне дослідження розподілу електронів за швидкостями

Теоретичні міркування:

Статистичний метод опису стану макроскопічних тіл або термодинамічних систем [1.11-3.11] спирається на визначення статистичних закономірностей випадкового (теплового) руху молекул. Не дивлячись на те, що змінні величини (координати та швидкості), які описують рух взаємодіючих атомів і молекул, змінюються випадково і передбачити їх величини в наступний момент часу неможливо, про те зміна їх середніх значень відбувається закономірно. Так само закономірно змінюються і інші відповідні функції від цих змінних.

Параметри термодинамічних систем, що ми їх спостерігаємо і вимірюємо (макропараметри: температура, тиск та інш.) визначаються як середні значення відповідних функцій змінних, які описують рух взаємодіючих атомів і молекул. Тому при статистичному опису стану макроскопічних тіл або термодинамічних систем, які складаються з великої кількості частинок, застосовують імовірнісну трактовку процесів, зокрема метод Гіббса.

Наприклад, якщо термодинамічна система складається з N однакових, взаємодіючих між собою, частинок то стан кожної з них можна описати значенням координати – радіус-вектора та імпульса . Повна сукупність радіус-векторів та імпульсів всіх частинок описуватиме стан системи вцілому. Якщо частинки статистично незалежні, то можна вважати, що кількість можливих станів відповідає кількості частинок. Тобто, імовірність кожного стану . В той же час статистично незалежні частинки можуть мати однакові стани в певних діапазонах значень радіус-векторів ( ) та імпульсів ( ), що свідчитиме про однакову імовірність цих станів. Тому необхідно говорити про функцію розподілу станів і про густину імовірності функції розподілу, яка визначатиме імовірність того, що частина dN із загальної кількості N часток, має параметри стану в діапазоні значень (r+dr, p+dp)

(1.11)

Для однорідної речовини, яка складається із статистично незалежних частинок, можна вважати m₁= m₂=…..= m_N, через що замість розподілу по імпульсам слід розглядати розподіл по швидкостям. При цьому, через статистичну незалежність розподілу по радіус-векторах і швидкостям, густина імовірності функції розподілу буде дорівнювати добутку відповідних функцій розподілу

. (2.11)

Це буде справедливим, якщо на час визначення параметрів термодинамічної системи вони будуть незмінні – система набуде стаціонарного стану, або, як кажуть, настане термодинамічна рівновага, для якої діятиме принцип детальної рівноваги. Принцип детальної рівноваги стверджує, що при термодинамічній рівновазі будь-який процес в системі може бути скомпенсований таким самим процесом, що відбувається в протилежному напрямку, тобто у термодинамічно врівноваженій системі імовірність прямого і оберненого процесів однакова.

Якщо це не виконуватиметься, то в системі виникнуть впорядковані рухи і процеси (дифузія, теплопередача та інш.), що порушить умови термодинамічної рівноваги.

У термодинамічно врівноваженій системі, таким чином, густина імовірності функції розподілу по радіус-векторах повинна бути постійною величиною, тобто стани всіх частинок розрізнятимуться лише за величиною швидкості руху, а не за місцем положення.

Через хаотичність теплового руху при термодинамічній рівновазі функція розподілу по швидкостях повинна залежати від величини вектора швидкості і не повинна залежати від спрямування цього вектора.

(3.11)

Крім того, при парній взаємодії частинок в хаотичному русі має виконуватись

(4.11)

Де : v₁, v ₂ – швидкості «першої» і «другої» частинок до взаємодіїї, а «штриховані» величини, відповідно після взаємодіїї.

Врахувавши (3.11) та інваріантність функції розподілу що-до вибраної системи координат можна стверджувати

. (5.11)

в термодинамічно врівноваженій системі виконується закон збереження енергії

. (6.11)

Прологарифмуємо вираз (5.11) і порівняємо результат з (6.11).

.

З цього порівняння випливає, що функція густини імовірності розподілу повинна мати вигляд

. (7.11)

Щоб отримати функцію розподілу по швидкостях у явному вигляді, необхідно, як це зробив Максвелл, використати визначення для «термодинамічної температури», закон розподілу енергії по степінях свободи , інтеграл Пуассона та умову нормування .

Після відповідних перетворень отримаємо вираз для густини імовірності розподілу частинок по компонентах швидкостей

. (8.11)

В практичних розрахунках найчастіше використовують функція розподілу Максвелла за абсолютними значеннями швидкостей

(9.11)

функція розподілу Максвелла за абсолютними значеннями швидкостей (Рис.1.11) має максимум при швидкості V_m , яка отримала назву «найбільш імовірна». Найбільш імовірну швидкість знаходять з умови екстремума функції розподілу(9.11); отримаємо .

значення середньої швидкості v можна знайти, вирахувавши інтеграл , а середньоквадратичної швидкості - вирахувавши інтеграл .

Експериментальне дослідження :

Експериментальне дослідження розподілу електронів за швидкостями грунтується на припущенні, що «вільні» електрони, які залишили метал в результаті термоелектронної емісії, поводять себе як ідеальний газ. Тому для них має бути характерний максвеллівський розподіл по швидкостях.

В даній роботі для дослідження характеру функції розподілу електронів за швидкостями використовується метод «затримуючого потенціалу»[4.11].

С уть методу полягає в наступному: В електронній лампі з розпеченим катодом (Рис.2.11)термоелектрони накопичуються у вигляді електронної хмари над поверхнею катоду. В просторі між катодом та анодом вони знаходяться в стані термодинамічної рівноваги – з катоду поступають емітовані електрони, а ті, що втратили частково свою енергію, повертаються на катод.

Частина електронів досягає аноду і створює в зовнішньому колі електричний струм. Для даної геометрії електродів електронної лампи має сенс використовувати циліндричну систему координат для запису параметрів руху електронів у міжелектродному просторі. Причому для розрахунку сили струму слід брати до уваги лише радіальну складову швидкості електронів V_R , тому що кутова складова V_φ не даватиме внесок у загальний струм. Крім того, приклавши до анода невелику позитивну напругу відносно катоду, можна практично всі електрони спрямувати в радіальному напрямку. Тому рівняння для густини імовірності розподілу електронів по компонентах швидкостей (8.11) перетвориться в рівняння лише для радіальної складової V_R.

Якщо в проміжку між анодом і катодом створити гальмуюче радіальне електричне поле, подавши на сітку негативний потенціал Ug відносно катоду, то аноду досягнуть лише ті електрони, радіальна складова швидкості яких, задовольнятиме умові

. (10.11)

де : m та e - маса і заряд електрона відповідно.

Тобто, сітка лампи виконуватиме роль аналізатора швидкостей, а сила анодного струму буде мірою кількості електронів dN , які мають швидкість, більшу за .

Якщо припустити, що розподіл радіальних складових швидкостей електронів відповідає розподілу Максвелла, то силу струму, що її створюють електрони із швидкостями , можна вирахувати, оцінивши кількість електронів N(V_R), які падають на одиницю площі аноду за одиницю часу

(11.11)

Де: N₀ – сумарна кількість електронів, які падають на одиницю площі аноду за одиницю часу при відсутності гальмівного поля в проміжку сітка-катод (Ug=0) . Якщо площа поверхні анода дорівнює S, то сила струму І в анодному колі буде дорівнювати

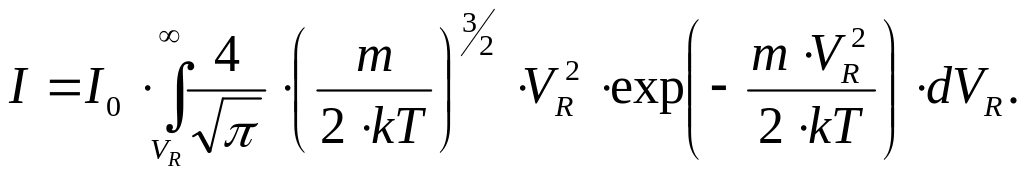де: . (12.11)

Звідси отримаємо остаточно

(13.11)

Таким чином, як випливає з (13.11), визначивши експериментально залежність сили анодного струму І від затримуючого потенціалу Ug, отримаємо функцію І =F(Ug), диференціал від якої з точністю до сталої співпадає з функцією розподілу Максвелла.

Експериментальне дослідження розподілу електронів по швидкостях.

Е

кспериментальне дослідження розподілу електронів по швидкостях виконується методом «затримуючого потенціалу» на установці, схема якої показана на Рис.3.11. В лабораторній роботі використовується електронна лампа – пентод, з трьома сітками. Перша сітка g₁ з'єднана з катодом опором R₁ що забезпечує еквіпотенційність проміжку катод - перша сітка, і, як наслідок, відсутність впливу зовнішніх електричних полів на термоелектрони. Електрони з радіальною складовою швидкості V_R попадають в простір між першою g₁ і другою g₂ сітками, де створене джерелом живлення U_С гальмуюче електричне поле. Опір R₂ забезпечує еквіпотенційність проміжку між другою g₂ та третьою g₃ сітками. Електрони, що подолали гальмуючу дію електричного поля сітки g₂ , пролітають крізь сітку g₃ і, будучи захоплені прискорюючим електричним полем, що створене анодним джерелом живлення U_А , попадають на анод. Сила анодного струму контролюється мікроамперметром І_А. Напруга на другій сітці контролюється вольтметром U_С .

Змінюючи від'ємну напругу на сітці g₂ , можна регулювати силу анодного струму. регулюючи анодну напругу_, можна досягти умови, щоб майже всі термоелектрони, емітовані катодом, досягали анода при нульовій напрузі на сітці g₂ .

Виконання вимірювань і опрацювання результатів вимірювань:

1. Ввімкнути живлення установки і почекати 3-5 хвилин, поки розігріється катод пентоду;

2. Регулятором сіткової напруги встановити її нульове значення;

3. Регулятором анодної напруги встановити максимальне значення анодного струму (100 поділок);

4. Змінюючи сіткову напругу із кроком 0,1(0,05) вольта, вимірювати значення анодного струму;

5. Вимірювання завершити, коли сила анодного струму сягне нульового значення;

6. Результати вимірювань занести в Таблицю 1.11.

Таблиця 1.11.

№ п/п	UС (в)	І А (μA)	І(UС) / І0	V105 (м/с)
1 2 ….	0 0,1 ….

Примітка : І₀ – величина анодного струму при нульовому значенні сіткової напруги.;

7. За даними Таблиці 1.11. розрахувати відносну зміну анодного струму І(U_С)/І₀ і значення швидкості електронів V ; результат розрахунку занести в Таблицю 1.11.. При розрахунках прийняти до уваги, що (м/с);

8. Побудувати графік залежності величини І(U_С) від швидкості електронів V;

9. Методами чисельного диференціювання, використовуючи побудований графік, визначити значення величини . Чисельне диференціювання можна виконати безпосередньо по графіку або, використовуючи математичні програми ORIGIN , MCAD [5.11]; результати розрахунку занести в Таблицю 1.11..

10. При розрахунках прийняти до уваги, що (м/с)^-1 .

11. За даними Таблиці 1.11 побудувати графік розподілу електронів по швидкостях .

Д одаток: Методика чисельного диференціювання по графіку проілюстрована наведеною нижче схемою :

Звідси розраховуємо величини

та .

Контрольні запитання:

1. Що означає термін «термодинамічна рівновага» ?

2. В чому полягає «принцип детальної рівноваги» ?

3. Що означає поняття «функція розподілу» фізичної величини?

4. Запишіть вираз для функції розподілу по швидкостях Максвелла.

5. Що означає термін «найбільш імовірна швидкість» і як її визначити ?

6. Що означає термін «середня швидкість» і як її визначити ?

7. Що означає термін «середньоквадратична швидкість» і як її визначити ?

8. Що у молекулярно-кінетичній теорії характеризує «середня швидкість»?

9. Що у молекулярно-кінетичній теорії характеризує «середньоквадратична швидкість»?

10. У який спосіб в молекулярно-кінетичній теорії вводиться поняття «термодинамічна температура»?

ЛІТЕРАТУРА

1.11. Кучерук І.М., Горбачук І.Т., Луцик П.П.. Загальний курс фізики: Навчальний посібник. –Т. 1.: Механіка. Молекулярна фізика і термодинаміка. – К.: Техніка, 1999. – 536 с.

11. Дущенко В.П., Кучерук І.М. Загальна фізика. Молекулярна фізика і термодинаміка. – К.: Вища школа, 1993. – 431 с.

11. Загальна фізика. Лабораторний практикум: Навч. посібник за заг.ред. І.Т. Горбачука. – К.: Вища школа, 1992. – 509 с.

4.11. Трофимова Т.И. Курс физики. – М.: Высш. шк., 2000. – 478 с.

5.11. Опрацювання результатів вимірювання при виконанні лабораторних робіт фізичного практикума з використанням математичної системи Mcad. (Методичні вказівки до лабораторного практикуму для студентів усіх спеціальностей) . А.О.Потапов, А.І.Мотіна. - К.: КНУТД, 2004.- 112 с.