40

Министерство образования и науки РФ

Государственное образовательное учреждение

высшего профессионального образования

«Тульский государственный университет»

Кафедра «Электронных Вычислительных Машин»

Сборник методических указаний к лабораторным работам

по дисциплине

Основы теории управления

Специальность: 090105 «Комплексное обеспечение информационной безопасности автоматизированных систем»

Форма обучения: очная

Тула 2010 г.

Методические указания к лабораторным работам составлены доц. каф ЭВМ Лебеденко Ю.И. и обсуждены на заседании кафедры ЭВМ факультета кибернетики

протокол № 15 от "_18_"____мая_____ 2010 г.

Зав. Кафедрой _______________________ в.С. Карпов

Методические указания к лабораторным работам пересмотрены и утверждены на заседании кафедры ЭВМ факультета кибернетики,

протокол №___ от "___"______________ 201_ г.

Зав. Кафедрой _______________________ в.С. Карпов содержание

Введение………………………………………………………………………………………..3

Лабораторная работа 1

Составление уравнений систем автоматического управления……………………….4

Лабораторная работа 2

Решение дифференциальных уравнений системы управления с помощью преобразования Лапласа ……………………………………………………………………………9

Лабораторная работа 3

Элементарные звенья динамических систем. Временные характеристики звеньев ………………………………………………………………………………………..12

Лабораторная работа 4

Преобразование структурных схем систем управления………………………..18

Лабораторная работа 5

Частотные характеристики линейных динамических систем ………………...24

Лабораторная работа 6

Анализ устойчивости линейных динамических систем ………………………..30

Лабораторная работа 7

Анализ точности автоматических систем …………………………………… …35

Библиографический список ………………………………………………………………………….. 40

Введение

Данные методические указания предназначены для студентов специальности 090105 «Комплексное обеспечение информационной безопасности автоматизированных систем», изучающих основы теории управления в качестве общепрофессиональной дисциплины в седьмом учебном семестре. Предполагается, что студенты обладают необходимыми знаниями по высшей математике, физике, электротехнике и основам электроники.

Поскольку основным методом исследования систем управления является их моделирование, то для выполнения лабораторных работ предполагается применять современные средства в виде персонального компьютера, оснащенного исследовательским программным пакетом MatLab (v.6.0 и выше). В ходе выполнения работы студенты уточняют основные теоретические положения, а затем решают практическую задачу, поставленную преподавателем.

После выполнения работы студент оформляет отчет, в котором указываются название работы, ее цель и основные задачи, отображается порядок выполнения работы, подтверждаемый реальными вычислениями, результаты выполнения, иллюстрируемые полученными формулами, таблицами и графиками.

Лабораторная работа1

Составление уравнений систем автоматического управления

1. Цель работы

Ознакомиться с порядком и правилами составления дифференциальных уравнений автоматической системы, с функциями и командами системы MatLab. Получить навыки численного решения дифференциальных уравнений в программной системе MatLab.

2. Теоретические положения

При составлении дифференциальных уравнений систем автоматического управления всегда используются физические законы, описывающие конкретное техническое устройство, механизм, прибор. Порядок составления дифференциальных уравнений системы лучше всего рассмотреть на примере.

Рассмотрим следящий электромеханический привод (рис.1.1):

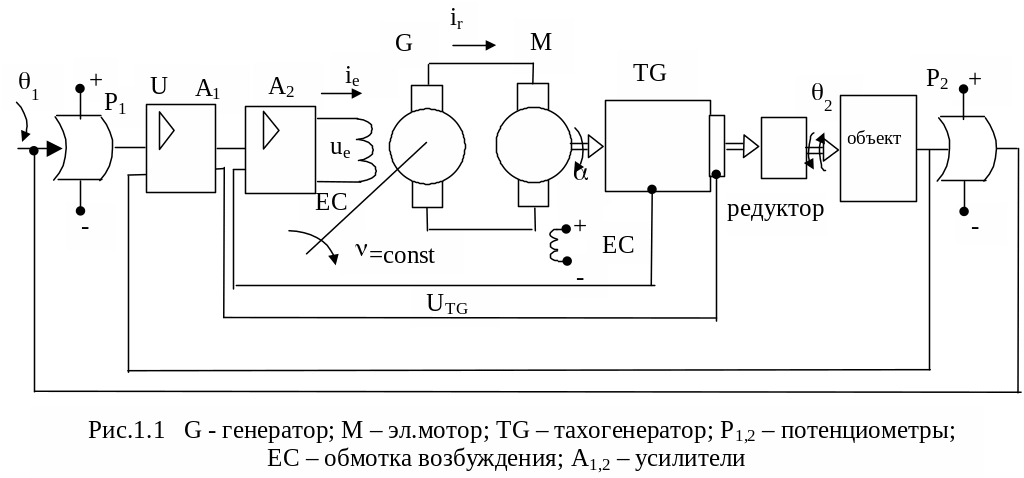
В этой системе _- входной угол; _ - выходной угол поворота объекта управления. Их разность (_ -_)служит сигналом управления для двигателя.

Для каждого отдельного узла сервопривода можно написать дифференциальное или алгебраическое уравнение:

1. Чувствительный элемент:

Выходное напряжение потенциометра P₁ определиться как

U₁=k₁₁.

На выходе P₂ имеем:

U₂=k₁₂,

где k₁-коэффициент передачи потенциометра. Следовательно

U=U₁-U₂=k₁(₁-₂)=k₁.

2. Усилители. Если рассматривать их как безынерционные элементы с помощью коэффициентами передачи k₂ и k₃, то с учетом того, что на входе второго усилителя выход первого суммируется с сигналом обратной связи тахогенератора, получим:

U_e=(k₂U-U_tg)k₃

3. Обмотка возбуждения генератора. Дифференциальное уравнение можно записать на основе закона Кирхгофа:

где L_e и r_e –величины индуктивности и активного сопротивления обмотки.

4. Генератор. Для генератора с линейной характеристикой ЭДС может быть вычислена по формуле:

e=k₅i_e; ;

5. Электродвигатель имеет две степени свободы. Соответственно, его описание будет иметь два дифференциальных уравнения первого порядка:

- для электрической части

- для механической части.

где L_r и r_r – индуктивность и активное сопротивление обмотки ротора,

С’_E и С’_М - коэффициенты пропорциональности,

J – момент инерции, приведенный к оси двигателя,

 - угловая скорость ротора,

M – момент нагрузки.

Если считать магнитный поток возбуждения двигателя постоянным, =const, то

где U_nom, M_nom, I_{r nom} – номинальные значения напряжения ан двигателе, вращающего момента и тока якоря;

₀ – угловая скорость ротора без нагрузки.

Угол вращения двигателя связан со скоростью через простое соотношение

.

6. Редуктор. Если характеристика механизма линейная, то ее можно описать алгебраическим выражением:

где q – коэффициент передачи редуктора.

7. Тахогенератор. Выходное напряжение этого устройства пропорционально скорости вращения двигателя:

Объединим все уравнения компонентов в единую систему

В этой системе в качестве входного воздействия выступает θ₁[rad], как возмущающее воздействие . В ней можно выделить четыре независимых переменных: θ₂[rad] – выход; Ω [rad/s]; i_r[A] и i_e[A].

Выведенные уравнения можно привести к относительным единицам. Для этого примем в качестве основной одну из фазовых переменных (чаще всего это выходная величина), измеряемую в конкретных физических единицах.

После этого можно пересчитать все коэффициенты в уравнениях так, чтобы они выражались в безразмерных единицах:

Пусть i_e = x₁; i_r = x₂; Ω = x₃; α = x₄; θ₁ = y₁; M = y₂.

Тогда

Легко видеть, что многие K_ij равны нулю в системе (2).

будем называть фазовыми координатами.

Для данной системы можно записать одно дифференциальное уравнение четвертого порядка

,

В общем виде:

(a₄p⁴+a₃p³+a₂p²+a₁p+a₀)x=y₁b₁+y₂b₂ (3),

или в еще более отвлеченной форме:

D(p)x(t)=Q(p)g(t)+N(p)f(p).

Это уравнение дает сокращенную форму записи дифференциальных уравнений системы через передаточные функции.

Для решения дифференциальных уравнений систем автоматического управления можно использовать систему MatLab.

Основное окно системы MatLab называется командным окном, в котором имеется традиционное для Windows-приложений меню и клиентская часть с символом приглашения >>. Также имеется полоса прокрутки окна.

После приглашения с клавиатуры можно вводить числа, имена переменных, знаки операций, которые составляют выражение. Имена переменных должны начинаться с буквы, могу включать цифры и символы подчеркивания.

После выполнения команды информация из зоны редактирования переходит в верхнюю часть окна, являющуюся зоной просмотра. Оттуда с помощью буфера обмена информация может быть помещена в зону редактирования или в другие приложения. Зона редактирования может быть расширена до двух и более строк после символа >> путем набора трех и более точек., однако в предыдущих строках уже при этом нельзя ничего менять. Команда clc позволяет очистить видимое пространство командного окна, но это не затронет памяти командного окна.

Кроме основного вся информация о ранее произведенных действиях может быть отразена также с помощью окон Command History и WorkSpace. Обратившись к ним с помощью мыши можно повторить ввод переменной или выражения в зону редактирования.

Неиспользуемые переменные можно очистить из памяти командного окна используя команду clear, а просмотреть список имеющихся переменных - командой who.

Введенную информацию можно сохранять и загружать из файлов системы, имеющих расширение .mat.

Особо важную роль в записи выражений играет точка с запятой. Во-первых, ставя её в конце выражения, можно не выводить результат на экран, что используется при промежуточных вычислениях. Во-вторых, точка с запятой работает как разделитель, когда несколько введенных выражений будут вычисляться одним нажатием клавиши Enter.

В системе MatLab присутствуют все основные элементарные функции:

^ -возведение в степень; sqrt – извлечение квадратного корня; exp – возведение в степень числа е; pow2 – степень числа 2. Также присутствуют обратные к ним функции: log – натуральный логарифм; - log10 - десятичный логарифм; log2 - по основанию 2. Тригонометрические функции также представлены весьма полно: sin, cos, tan, cot и обратные к ним: asin, acos, atan, acot.

Для решения таких систем в MatLab имеются «интеллектуальные решатели». Это функции ode23, ode45, ode113, ode15s, ode23s, ode23t, ode23tb. Функции с суффиксом s предназначены для решения так называемых систем жестких дифференциальных уравнений, а для остальных наиболее употребительной является функция ode45, реализующая алгоритм Рунге-Кутта 4-5 порядков (разные порядки используются в нем для контроля шага интегрирования).

Для применения функции необходимо записать дифференциальные уравнения в нормальной форме Коши:

y1’=F1(x, y1, y2, …, yn);

y2’=F2(x, y1, y2, …, yn);

……………………….

yn’=Fn(x, y1, y2, …, yn);

Введем вектор-столбцы Y и F, состоящие из y1, y2, …yn и F1, F2, …Fn соответственно. Тогда в векторной форме система дифференциальных уравнений примет вид:

Y’=F(x, Y);

Чтобы применить решатель ode45 надо оформить в виде собственной M-функции правую часть системы уравнений.

Пусть, например, необходимо решить систему дифференциальных уравнений:

y1’=y2+K*x*x;

y2’=-y1;

с начальными условиями у(0)=0, у’(0)=1. Неизвестная вектор-функция Y состоит из двух элементов Y=[y1, y2].

Т.к. функции у1 и у2 вычисляются во многих точках в процессе нахождения решения, то реально у1 и у2 являются векторами-столбцами. Вектор правых частей F системы уравнений для К=0,01 вычисляем с помощью собственной M –функции MyDifEq1:

Function F = MyDifEq1( x, y)

F= [ 0.01*c*c +y(2); -y(1) ];

Текст которой записываем в файл MyDifEq1.m . Она вызывается каждый раз, когда требуется вычислить правые части в конкретной точке х, так что здесь х является скаляром, а вектор у состоит всего из двух элементов.

Решение дифференциальных уравнений хорошо визуализировать с помощью функции построения графиков plot:

plot(t,y(:,1),'-',t,y(:,2),'--');

3. Варианты заданий на работу

1) Операционный усилитель имеет обратную связь с RC-цепью (рис.1.2)

Составить систему дифференциальных уравнений объекта и получить их решение на ограниченном интервале времени с помощью системы MaLab.

Ответ: .

2) Выполните задание по варианту 1, если в обратной связи стоит только конденсатор C.

Ответ: .

3) Произведите моделирование электрической части системы, соответствующей рис.1.1. при параметрах системы и начальных условиях, заданных преподавателем.

4) Произведите моделирование механической части системы, соответствующей рис.1.1. при параметрах системы и начальных условиях, заданных преподавателем.

4. Контрольные вопросы

1. Что называется динамической системой?

2. Приведите основные признаки классификации динамических систем.

3. Дайте определения объекта регулирования и регулятора.

4. Поясните принципы управления по разомкнутому и замкнутому контуру.

5. В чем различие между прямым и непрямым регулированием?

6. Перечислите основные функциональные элементы системы автоматического регулирования.

7. Как осуществляется переход от физических узлов системы к их математическому описанию?

8. Почему к системам автоматического управления часто применяется процедура линеаризации?

9. Что называется безразмерной системой уравнений?

10. Для чего служит передаточная функция системы?

Лабораторная работа 2