Контрольные вопросы к теме №5

1. Что называется средней величиной в статистике?

2. Способы определения средней арифметической величины.

3. Основные свойства средней арифметической.

4. Что такое мода и способы ее расчета.

5. Что такое медиана и способы ее расчета.

Тема 6. Статистическое изучение динамики социально-экономических явлений Лекция 7. Статистическое изучение динамики социально-экономических явлений

Основные понятия:

динамика; ряд динамики; коэффициент роста; абсолютный прирост; темп роста; темп прироста; коэффициент опережения; абсолютное значение 1% прироста; средний уровень ряда; метод скользящей средней; прогнозирование; интерполяция; сезонные колебания; индекс сезонности.

Развитие общественных явлений во времени называется динамикой. Ряды статистических показателей, характеризующих развитие общественных явлений во времени, называются рядами динамики. Значение рядов динамики состоит в том, что они дают возможность выявить закономерности развития явлений, облегчают их анализа. Каждый ряд состоит из 2-х граф: в одной указываются периоды или даты времени, во второй – числовая характеристика изучаемого явления в эти периоды, называемая уровнем ряда. Уровни ряда могут выражаться абсолютными, средними и относительными величинами. Временные ряды, состоящие из абсолютных величин, могут быть двух видов: интервальные и моментные. В интервальном ряду приводятся данные, характеризующие состояние явления за данный период времени.

Таблица 17

Производство пиломатериалов

Годы	2003	2004	2005	2006	2007
Пиломатериалы, тыс. м3	2371	2727	2737	2507	2435

Особенностью интервальных рядов динамики является то, что данные этих рядов можно суммировать и получать новые численные значения, относящиеся к более длительным периодам времени.

Моментный ряд динамики состоит из показателей, характеризующих состояние явления на определенные моменты времени.

Таблица 18

Запас топлива на складах

Дата	на 1.01	на 1.02	на 1.03	на 1.04
Запас топлива, т	13,8	12,8	15,0	17,0

Уровни моментных рядов складывать нельзя, так как слагающие явления единицы последовательно повторяются в различных уровнях ряда, поэтому их сумма не имеет смысла.

К суммированию показателей интервального ряда часто прибегают для построения рядов динамики с нарастающими итогами.

Таблица 19

Добыча угля за январь-июль

По месяцам	I	II	III	IV	V	VI	VII
По месяцам, т	40	36	42	42	45	45	48
Нарастающий итог с начала года	40	76	118	160	205	250	298

Нарастающие итоги часто приводятся в отчетах предприятий.

Если ряд динамики состоит из относительных или средних величин, то суммировать их нельзя, но разность их имеет реальный смысл.

Таблица 20

Уровень механизации погрузочно-разгрузочных работ

(в % к общему объему работ)

Годы	1985	1990	1995	2000	2005
Уровень, %	31	67	79	87	89

Уровень механизации за период 1985–2005 гг. повысился на 58 пунктов (89–31). Пунктом в статистике называется разность в 1 процент. Уровень интенсивности этого роста определяется так: 89% : 31% = 2,87 (287 – 100 = 187%) или эту величину можно получить путем отнесения разности в пунктах к тому уровню, с которым производится сравнение: 58 : 31 = 1,87%.

Для правильного построения рядов динамики необходимо соблюдать ряд требований:

1) Все показатели ряда динамики должны быть достоверными, точными, научно обоснованными.

2) Все показатели ряда должны быть сопоставимы. Основным условием сопоставимости статистических показателей является одинаковая методология их определения.

3) Показатели ряда динамики должны быть сопоставимы по территории, к которой они относятся.

4) Показатели ряда динамики должны быть сопоставимы во времени, т.е. они должны быть исчислены за одни и те же периоды времени или же на одну и ту же дату.

5) Все показатели ряда должны быть приведены в одних и тех же единицах измерения.

6) Должна соблюдаться сопоставимость цен.

При изучении рядов динамики статистика решает ряд задач:

1) измеряет абсолютную и относительную скорость роста либо снижения уровня за отдельные промежутки времени;

2) дает обобщающие характеристики уровня и скорости его изменения за тот или иной период;

3) выявляет и численно характеризует основные тенденции развития явления на отдельных этапах;

4) дает сравнительную числовую характеристику развития данного явления в разных регионах или на разных этапах;

5) выявляет факторы, обуславливающие изменение изучаемого явления во времени;

6) делает прогнозы развития явления в будущем.

Для сравнения между собой отдельных уровней ряда динамики рассчитываются следующие показатели: абсолютные приросты, темпы роста (коэффициенты роста), темпы прироста и абсолютное значение одного процента прироста. Расчет этих показателей основан на сравнении между собой уровней ряда динамики. При этом уровень, с которым производится сравнение, может быть базисным или цепным.

Абсолютный прирост показывает, насколько в абсолютном выражении уровень отчетного периода больше или меньше уровня базисного периода. Абсолютный прирост рассчитывается как с постоянной, так и переменной базой сравнения. Абсолютный прирост за единицу времени измеряет абсолютную скорость роста или снижения уровня.

(переменная база сравнения);

(постоянная база сравнения);

– уровень ряда, принятого за базу сравнения.

Коэффициент роста, темп прироста и абсолютное значение 1% прироста характеризуют интенсивность процесса роста.

Коэффициент роста показывает, во сколько раз уровень отчетного периода больше или меньше уровня базисного и рассчитывается как с переменной, так и с постоянной базой сравнения.

С переменной базой сравнения , с постоянной базой сравнения . Коэффициент роста может быть больше единицы, меньше единицы, равен единице. Коэффициенты роста, выраженные в процентах, носят название темпов роста.

,

.

Ели коэффициенты роста, рассчитанные с переменной базой сравнения, характеризуют изменение явления от периода к периоду, то коэффициенты роста с постоянной базой – непрерывную линию развития.

Темп прироста показывает, на сколько процентов уровень отчетного периода больше или меньше уровня базисного.

При переменной базе сравнения:

или или .

При постоянной базе сравнения:

или .

Абсолютное значение 1% прироста (А_1%):

или .

Между показателями динамики, вычисленными с постоянной и переменной базой, существует определенная связь.

Сумма абсолютных приростов с переменной базой дает общий прирост за исследуемый период:

,

где n – число уровней динамики ряда.

Например, имеются данные об уровне явления за четыре периода: y₁, y₂, y₃, y₄.

Цепные абсолютные приросты:

Взаимосвязь между базисными и цепными коэффициентами роста такова: произведение последовательных цепных коэффициентов роста равно базисному коэффициенту роста, а частное от деления последующего базисного коэффициента роста на предыдущий равно соответствующему цепному коэффициенту роста.

Цепные коэффициенты роста:

;

,

где − базисные коэффициенты роста.

При сопоставлении динамики развития двух явлений можно использовать показатель, предоставляющий собой отношение темпов роста за одинаковые отрезки времени по двум динамическим рядам. Этот показатель называют коэффициентом опережения.

,

где , – соответствующие уровни сравниваемых динамических рядов. С помощью этого коэффициента могут сравниваться динамические ряды одинакового содержания, но относящиеся к разным территориям или к различным организациям или ряды разного содержания, характеризующие один и тот же объект.

Для получения обобщающей характеристики интенсивности развития явления за длительный период исчисляют средние показатели динамики.

Средний уровень ряда динамики исчисляется различно в зависимости от вида ряда. Для интервального ряда он рассчитывается по формуле средней арифметической простой:

,

где п – число уровней ряда.

Для моментного ряда с равными интервалами по формуле средней хронологической простой:

.

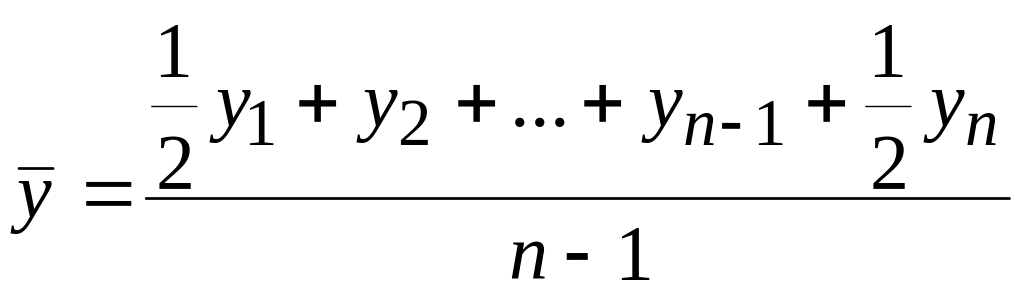Для моментного ряда с неравными интервалами по формуле средней хронологической взвешенной:

,

где t – промежутки времени.

Все остальные средние показатели для интервальных и моментных рядов динамики исчисляются одинаково.

Средний абсолютный прирост ( ) определяется по формуле средней арифметической из абсолютных приростов, исчисленных с переменной базой:

или ,

где , – конечный и начальный уровни динамического ряда.

Средний коэффициент роста определяется по формуле средней геометрической из коэффициента роста за отдельные периоды:

или ,

где n – число уровней ряда.

Средний темп роста представляет собой средний коэффициент роста, выраженный в процентах:

.

Средний темп прироста определяется, исходя из темпа роста:

или .

В практике статистики нередко возникает необходимость сравнения между собой рядов динамики двух или более родственных или взаимосвязанных явлений (уголь и нефть, шерсть и шелк). Для этого нужно преобразовывать абсолютные показатели сравниваемых рядов динамики в относительные, приняв показатели какого-либо одного года за 1 или 100. Такое преобразование рядов динамики, состоящее из абсолютных величин, в сопоставимые между собой ряда относительных величин, называется приведением их к общему основанию.

Таблица 21