3. Статистическое изучение динамики социально-экономических явлений
Для сравнения между собой отдельных уровней ряда динамики рассчитываются следующие показатели: абсолютные приросты, темпы (коэффициенты) роста, темпы прироста, абсолютное значение одного процента прироста. Расчет этих показателей основан на сравнении между собой уровней ряда динамики. При этом уровень, с которым производится сравнение, может быть базисным или цепным.
Абсолютный прирост (А) показывает, насколько в абсолютном выражении уровень отчетного периода больше или меньше уровня базисного периода.
(переменная
база сравнения);
(постоянная
база сравнения);
-
уровень ряда, принятого за базу сравнения.
Коэффициент
роста (
)
показывает, во сколько раз уровень
отчетного периода больше или меньше
уровня базисного периода.
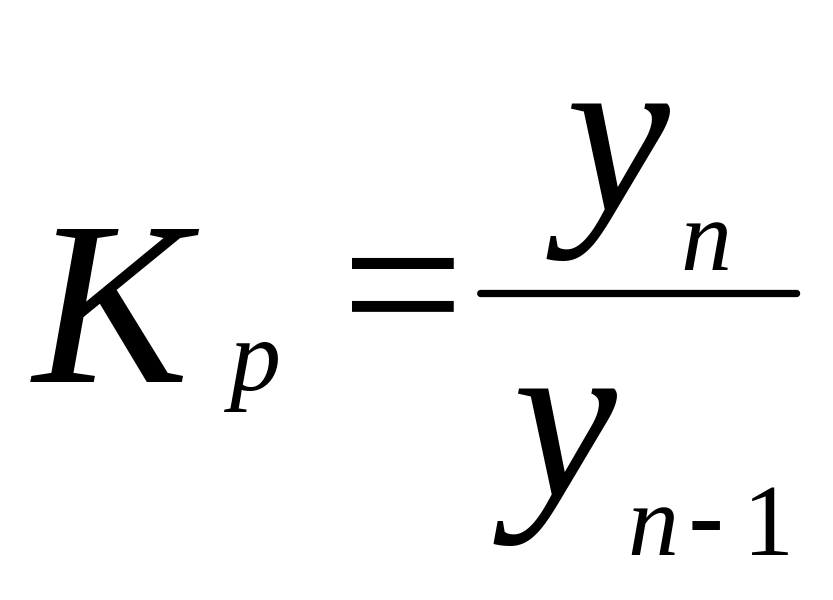или
.
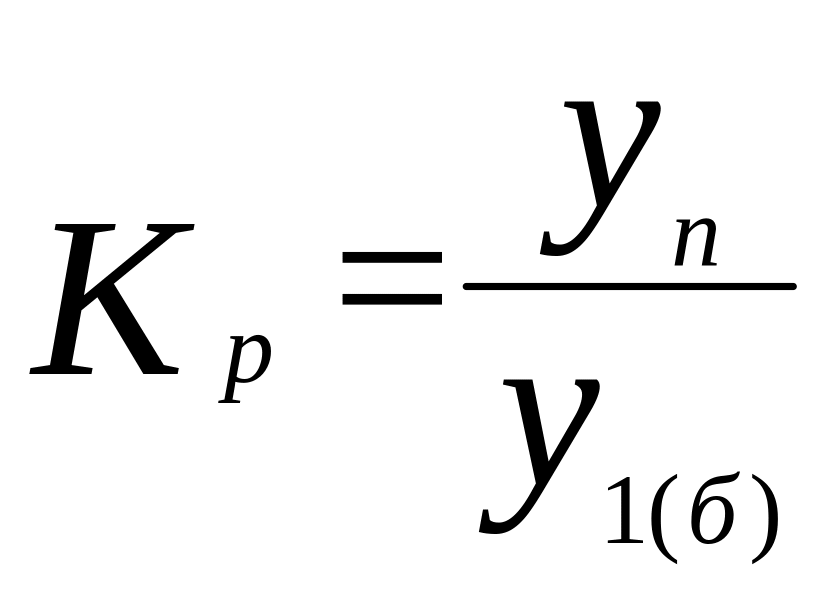Коэффициенты
роста, выраженные в процентах, носят
название темпов роста (
).
Темп
роста (
)
показывает, на сколько процентов уровень
отчетного периода больше или меньше
уровня базисного.
или
.
Абсолютное
значение 1% прироста (
)
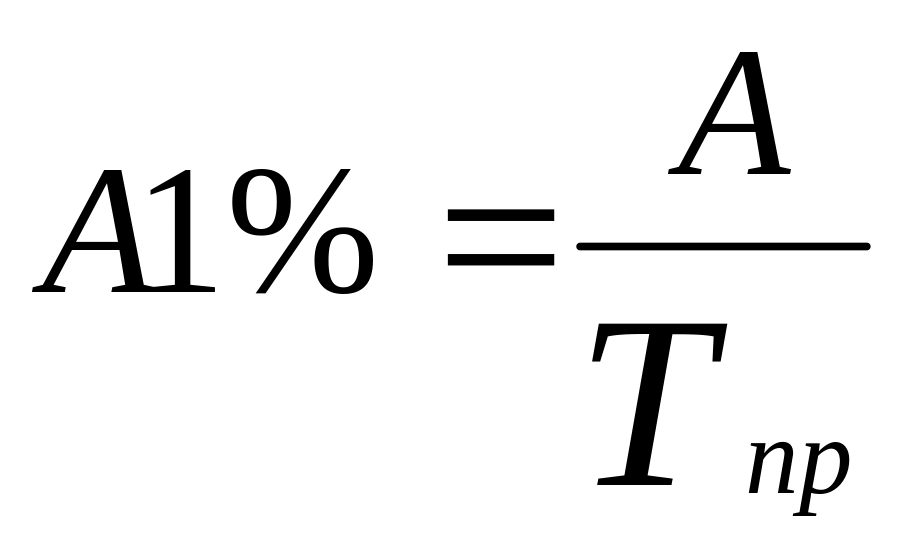или
.
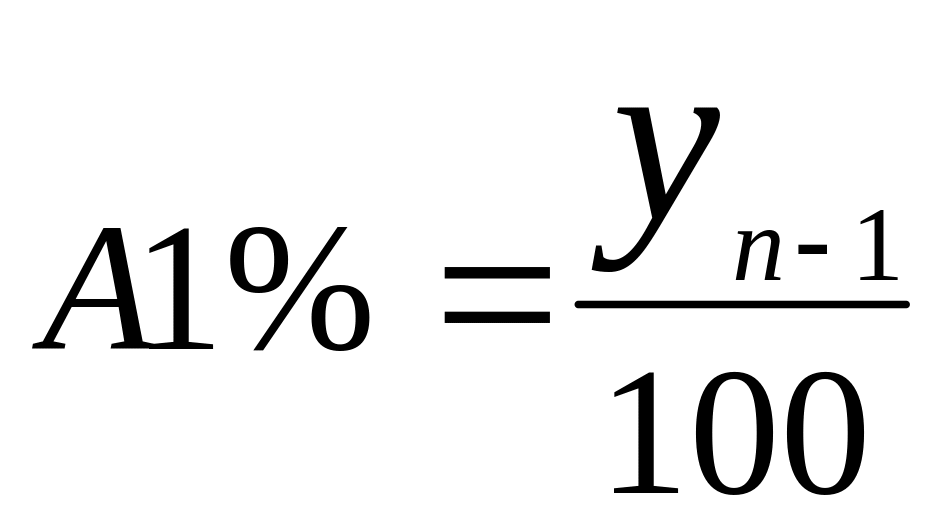Средний уровень ряда динамики исчисляется различно в зависимости от вида ряда. Для интервального ряда он рассчитывается по формуле средней арифметической простой
,
где n – число уровней ряда.
Средний
абсолютный прирост (
)
или
.
Средний коэффициент роста ( )
или
.
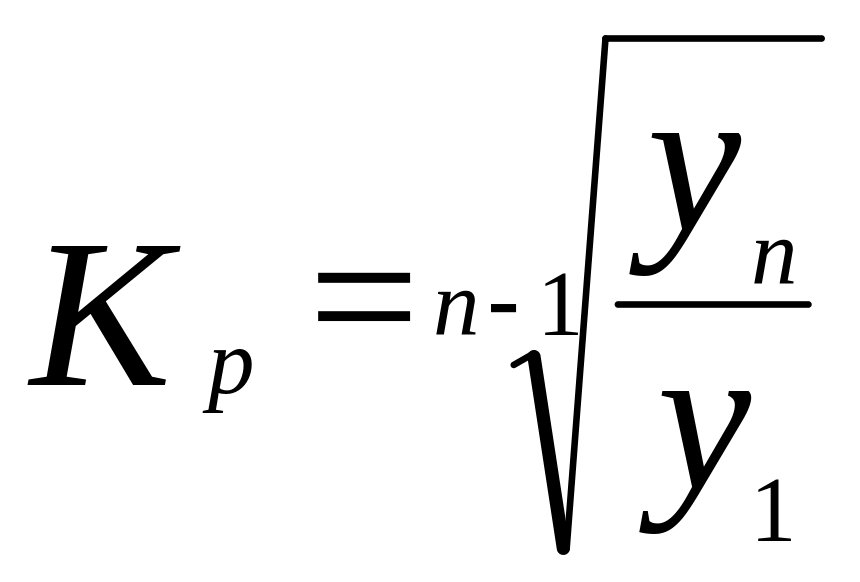Средний
темп роста
.
Средний
темп прироста
.
Метод скользящей средней заключается в том, что вычисляется средний уровень из определенного числа первых по порядку уровней ряда, затем – средний уровень из такого же числа уровней, начиная со второго и т.д.:
;
;
.
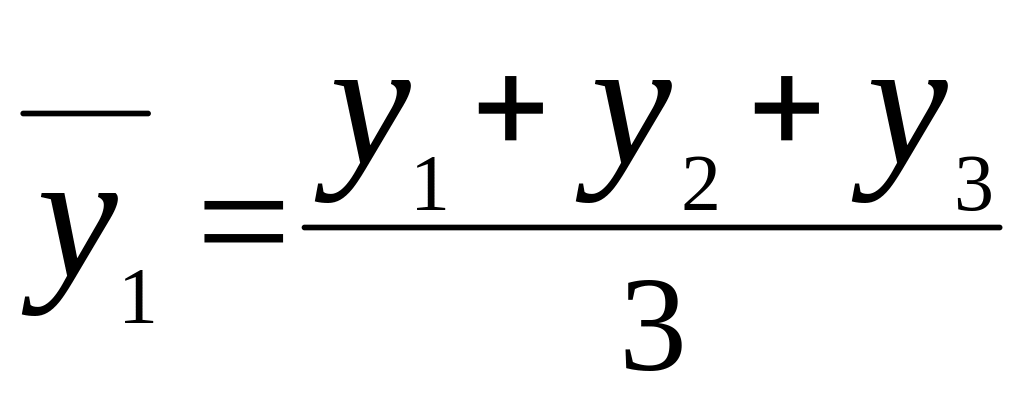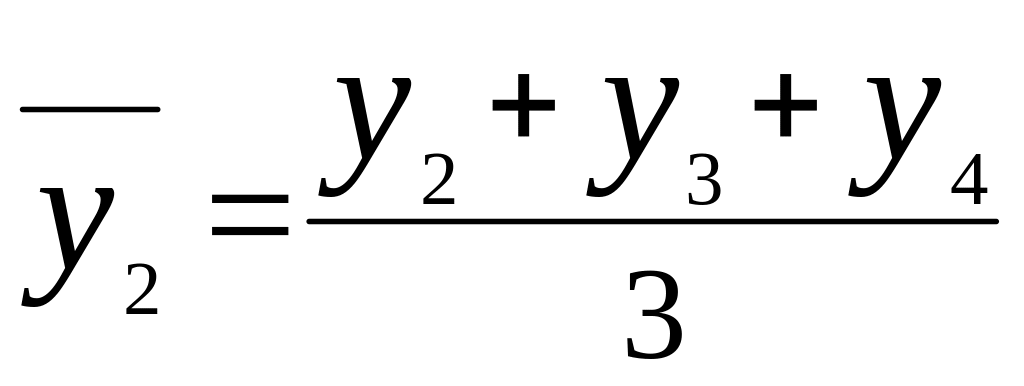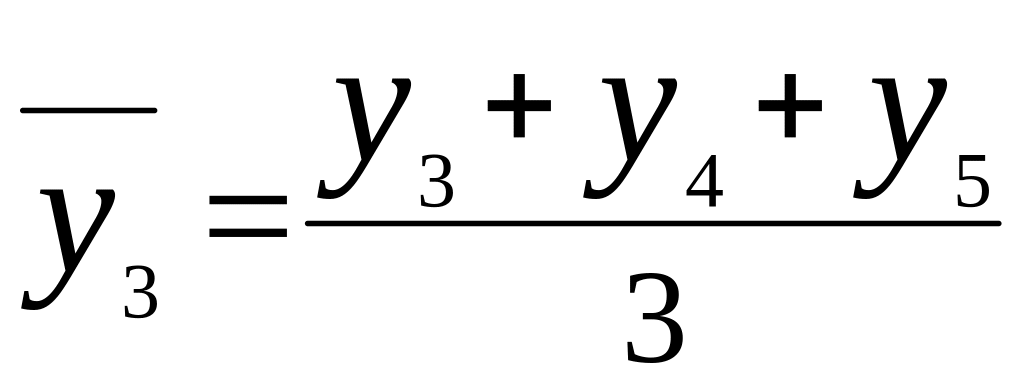Выравнивание
ряда по прямой предусматривает
решение следующего уравнения:
,
где t
– время (порядковый номер интервала
или момент времени).
Расчет
параметров значительно упрощается,
если
.
, следовательно
– средний уровень ряда;
, следовательно
– средний абсолютный прирост.
Глубину сезонных колебаний измеряют индексами сезонности (Iсез):
,
где 
– средняя из фактических средних уровней
одноименных месяцев;
– общая
средняя за исследуемый период.
Задача 1. Остатки вкладов населения города характеризуются следующими данными (млрд. руб.):
на 01.01. |
- 532,5 |
на 01.03. |
- 570,1 |
на 01.05. |
- 640,4 |
на 01.07. |
- 487,5 |
на 01.09. |
- 540,2 |
на 01.11. |
- 620,3 |
на 01.01. следующего года |
- 749,3 |
Рассчитайте средний остаток вкладов за I и II полугодие и за год.
Задача 2. Определите недостающие данные.
Год |
Производство продукции, млн. у.е. |
А, млн. у.е. |
Тр, % |
Тпр, % |
А1%, млн. у.е. |
2001 |
92,5 |
|
|
|
|
2002 |
|
1,8 |
|
|
|
2003 |
|
|
104,0 |
|
|
2004 |
|
|
|
5,8 |
|
2005 |
|
|
|
|
|
2006 |
|
7,0 |
|
|
1,15 |
Задача 3. Определите недостающие данные.
Год |
Фонд заработной платы, млрд. руб. |
А, млрд. руб. |
Тр, % |
Тпр, % |
А1%, млрд. руб. |
2002 |
143,2 |
|
|
|
|
2003 |
|
18,9 |
|
|
|
2004 |
|
|
|
5,4 |
|
2005 |
|
|
103,4 |
|
|
2006 |
|
|
|
1,2 |
|
Задача 4. Приведите ряд к сопоставимому виду.
Показатель |
2002 |
2003 |
2004 |
2005 |
2006 |
Численность, тыс. чел |
2468 |
2500 |
2560 |
- |
- |
В старых границах |
|||||
В новых границах |
|
|
2670 |
2720 |
2780 |
Годы
Задача 5. Приведите ряд к сопоставимому виду (млн. т).
Годы |
Мазут |
Торф |
2002 |
114 |
132 |
2003 |
100 |
111 |
2004 |
109 |
94 |
2005 |
124 |
101 |
2006 |
160 |
105 |
Задача 6. Отпуск тепловой энергии ТЭЦ за пять лет следующий:
Год |
2002 |
2003 |
2004 |
2005 |
2006 |
Отпуск теплоэнергии, Гкал |
2718 |
2891 |
3240 |
3621 |
3862 |
Определите ежегодные абсолютные приросты с постоянной и переменной базой, темпы роста и прироста, абсолютное значение 1% прироста.
Задача 7. Среднесписочный состав автомобильного парка предприятия характеризуется следующими данными:
списочное число автомобилей на 01.01. – 900 шт.;
поступило автомобилей 15.01 – 15 шт.; 22.01. – 3 шт.; 10.02. – 5 шт.;
списано автомобилей 24.01. – 4 шт.; 12.02. – 3 шт.
Определите изменение среднесписочного числа автомобилей в феврале и в январе.
Задача 8. Производство цемента характеризуется следующими данными:
Год |
1997 |
1998 |
1999 |
2000 |
2001 |
2002 |
2003 |
2004 |
2005 |
2006 |
Производство цемента, млн. т |
64 |
72 |
80 |
84 |
86 |
90 |
95 |
100 |
104 |
109 |
Выровнять ряд по прямой и использовать уравнение для экстраполяции уровней на 2009 г. Построить график первичного и выровненного рядов.
Задача 9. Определите показатели динамики по следующим данным.
Год |
1997 |
1998 |
1999 |
2000 |
2001 |
2002 |
2003 |
2004 |
2005 |
2006 |
Прибыль, млрд. руб. |
10,3 |
10,5 |
12,2 |
13,0 |
13,5 |
14,1 |
16,0 |
18,0 |
20,2 |
22,9 |
Задача 10. Имеются данные о выработке продукции по предприятию за первую половину сентября (в млн. руб.):
Дни месяца |
||||||||||||||
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
14 |
15 |
16 |
200 |
230 |
210 |
180 |
250 |
230 |
290 |
300 |
310 |
280 |
270 |
320 |
330 |
350 |
350 |
Произвести сглаживание ряда методом пятидневной скользящей средней и выровнять ряд по прямой. Представить на графике первичный и выровненные ряды.
Задача 11. Выполнить следующие расчеты: рассчитать показатели динамики с постоянной и переменной базой сравнения; рассчитать среднегодовые показатели динамики; произвести сглаживание ряда методом 3-х дневной скользящей средней; выровнять ряд по прямой; построить график искомого и выровненного ряда.
№ варианта |
Годы |
2000 |
2001 |
2002 |
2003 |
2004 |
2005 |
2006 |
Показатель |
||||||||
1 |
Мощность эл. станций, млн. кВт |
115,0 |
166,1 |
217,5 |
266,7 |
315,1 |
338,9 |
341,4 |
2 |
Мощность ТЭС, млн. кВТ |
92,8 |
133,8 |
172,1 |
201,9 |
225,1 |
239,7 |
239,6 |
3 |
Мощность ГЭС, млн. кВт |
22,2 |
31,4 |
40,9 |
52,3 |
61,7 |
63,8 |
64,3 |
4 |
Производство эл. энергии эл. станциями, млрд. кВт-ч |
506,7 |
740,9 |
1038,6 |
1293,9 |
1544,2 |
1705,0 |
1722,0 |
5 |
Производство эл. энергии ТЭС, млрд. кВт-ч |
425,2 |
612,8 |
892,4 |
1037,1 |
1162,3 |
1258,6 |
1285,9 |
6 |
Производство электроэнергии ГЭС, млрд. кВт-ч |
81,5 |
124,4 |
126,0 |
163,9 |
214,5 |
230,8 |
223,5 |
7 |
Выработка эл. энергии, млрд. кВт-ч |
33,2 |
36,3 |
37,8 |
38,2 |
38,2 |
39,5 |
38,7 |
8 |
Выпуск эл. оборудования распр. сетей, млн. руб. |
1549,3 |
1709,2 |
1926,7 |
2060,3 |
2404,4 |
2636,0 |
2491,9 |
9 |
Выпуск трансформаторов, млн. руб. |
767,2 |
757,3 |
890,2 |
1006,4 |
916,6 |
939,7 |
1162,7 |
10 |
Эл. оборудование пром. назначения, млн. руб. |
2975,1 |
3224,5 |
3796,8 |
4532,4 |
4209,1 |
4951,9 |
5613,2 |
Задача 12. По таксомоторному предприятию имеются следующие данные о величине платного пробега за 3 года (в тыс. км):
Месяц |
Год |
||
2004 |
2005 |
2006 |
|
Январь |
60,0 |
70,0 |
100,2 |
Февраль |
62,0 |
77,4 |
105,0 |
Март |
66,4 |
78,2 |
107,0 |
Апрель |
70,0 |
80,0 |
110,5 |
Май |
78,4 |
88,4 |
113,7 |
Июнь |
80,0 |
89,5 |
115,0 |
Июль |
80,3 |
90,3 |
116,4 |
Август |
86,5 |
94,6 |
120,0 |
Сентябрь |
79,0 |
94,0 |
118,7 |
Октябрь |
76,4 |
92,5 |
115,0 |
Ноябрь |
75,0 |
90,0 |
107,5 |
Декабрь |
70,4 |
85,5 |
98,2 |
На основе приведенных данных выявить наличие сезонной неравномерности и измерить ее степень.
Задача 12. На основе приведенных данных измерить сезонные колебания методом абсолютных разностей; методом относительных разностей; рассчитать индексы сезонности; изобразить графически сезонную волну.
Производство трансформаторов, тыс. шт.
Месяц |
Год |
||
2004 |
2005 |
2006 |
|
Январь |
199 |
190 |
223 |
Февраль |
224 |
208 |
229 |
Март |
221 |
201 |
219 |
Апрель |
211 |
250 |
196 |
Май |
180 |
184 |
188 |
Июнь |
248 |
215 |
232 |
Июль |
250 |
243 |
243 |
Август |
300 |
320 |
316 |
Сентябрь |
283 |
246 |
253 |
Октябрь |
236 |
226 |
251 |
Ноябрь |
259 |
241 |
222 |
Декабрь |
261 |
201 |
216 |
Задача 13. На основе приведенных данных измерить сезонные колебания методом абсолютных разностей; методом относительных разностей; рассчитать индексы сезонности; изобразить графически сезонную волну.
Потребление жидкого топлива, тыс. шт.
Месяц |
Год |
||
2004 |
2005 |
2006 |
|
Январь |
126 |
156 |
174 |
Февраль |
166 |
220 |
263 |
Март |
460 |
354 |
376 |
Апрель |
708 |
796 |
824 |
Май |
918 |
980 |
1020 |
Июнь |
1074 |
1120 |
1140 |
Июль |
866 |
840 |
870 |
Август |
774 |
702 |
736 |
Сентябрь |
750 |
858 |
796 |
Октябрь |
466 |
620 |
630 |
Ноябрь |
264 |
328 |
360 |
Декабрь |
114 |
224 |
300 |
Задача 14. На основе приведенных данных измерить сезонные колебания методом абсолютных разностей; методом относительных разностей; рассчитать индексы сезонности; изобразить графически сезонную волну.
Реализация электроосветительной аппаратуры, млн. руб.
Месяц |
Год |
||
2004 |
2005 |
2006 |
|
Январь |
12,7 |
16,3 |
30,8 |
Февраль |
11,5 |
17,4 |
24,1 |
Март |
12,0 |
18,4 |
21,2 |
Апрель |
45,6 |
78,9 |
73,1 |
Май |
40,4 |
67,3 |
69,9 |
Июнь |
60,0 |
66,6 |
77,7 |
Июль |
42,0 |
42,7 |
43,6 |
Август |
23,4 |
39,9 |
40,7 |
Сентябрь |
14,1 |
28,9 |
70,0 |
Октябрь |
14,6 |
25,2 |
40,7 |
Ноябрь |
16,3 |
27,9 |
32,7 |
Декабрь |
18,0 |
30,5 |
33,0 |
Задача 15. Вычислить средний остаток материалов на складе за первый квартал текущего года
Остаток материалов на складе, млн.руб. |
|||
На 1-е января |
На 1-е февраля |
На 1-е марта |
На 1-е апреля |
24,8 |
25,6 |
21,2 |
18,1 |