2. Средние величины
Средняя арифметическая простая исчисляется путем деления суммы значений признака на число значений:
,
где 
– средняя арифметическая;
– отдельные
значения признака;
– число
значений признака.
Если
данные представлены в виде дискретного
ряда распределения, то расчет средней
производится по формуле средней
арифметической взвешенной:
,
где х – значение признака;
f – частота повторения соответствующего признака (веса).
Средняя гармоническая представляет собой обратную величину средней арифметической из обратных величин. Она бывает простая и взвешенная:
Простая
–
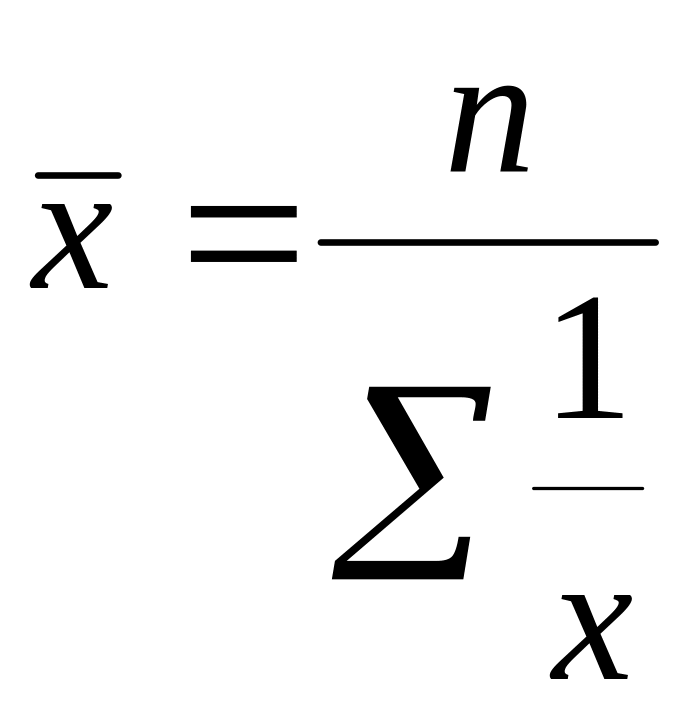
Взвешенная
–
,
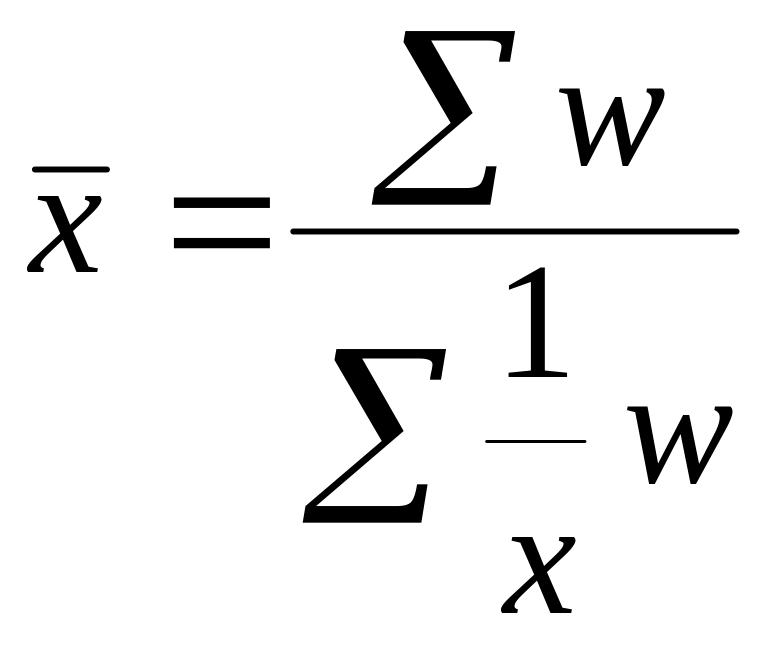Средняя квадратическая используется в том случае, когда необходимо возводить варианты в квадрат:
Простая
–
;
Взвешенная
–
.
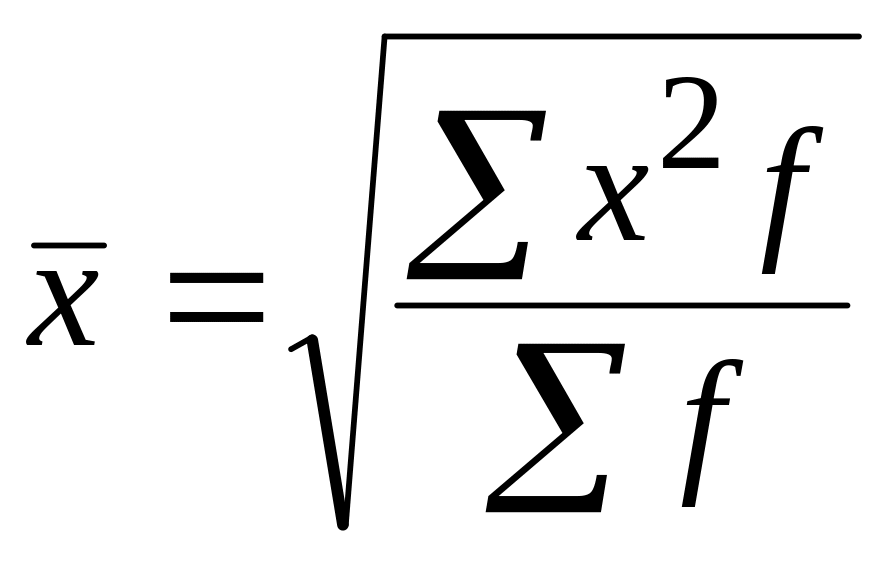Средняя
геометрическая –
.
Средняя хронологическая:
Простая
–
;
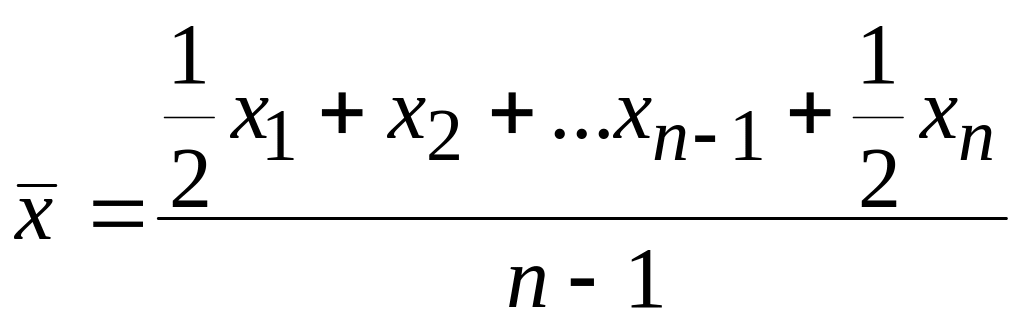взвешенная
–
.
Если
данные представлены в виде интервального
ряда распределения, предварительно
вычисляется среднее значение признака
для каждого интервала, представляющее
полусумму нижнего и верхнего значений
интервала
,
где 
;
– нижняя
граница интервала;
– верхняя
граница интервала.
Способ исчисления средней арифметической с использованием ее свойств известен в статистике как способ «условного нуля» или «условной средней», а также как «способ моментов».
Этот способ расчета находит отражение в следующей формуле:
.
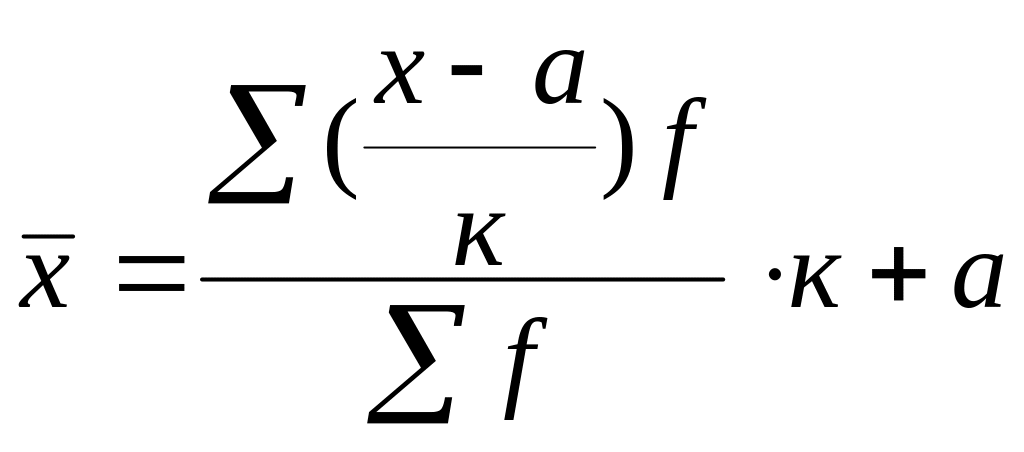Если
уменьшенные варианты
обозначить
через
,
то
.
Мода
– это наиболее часто встречающееся
значение признака в совокупности.
Медианой
называется
численное значение признака, расположенное
в середине ранжированного ряда, которое
делит этот ряд на две равные по численности
части. Для определения медианы сначала
находят ее место в ряду по формуле
,
где n
– число членов ряда (
).
Если число единиц четное, то место
медианы в ряду определяется как
.
Для определения моды в рядах с равными интервалами распределения модальный интервал определяется по наибольшей частоте, а в рядах с неравными интервалами – по наибольшей плотности распределения.
Для определения моды в рядах с равными интервалами используют формулу:
,
где 
– нижняя граница модального интервала;
– величина
интервала;
– частоты
предмодального, модального и послемодального
интервала.
Для расчета медианы в интервальном ряду воспользуемся следующими формулами:
,
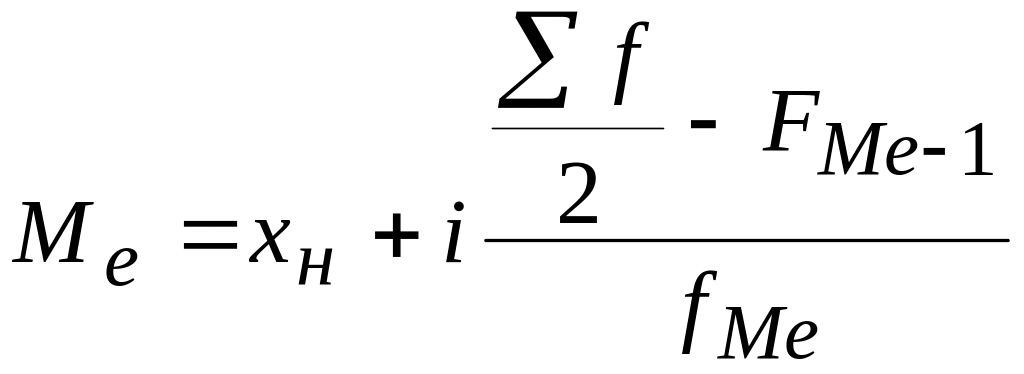или 
,
где 
– нижняя граница медианного интервала;
i – величина интервала медианного;
– порядковый
номер медианы;
– частота,
накопленная до медианного интервала;
– частота
медианного интервала.
– верхняя
граница медианного интервала;
– накопленная
частота медианного интервала.
Задача 1. Имеются следующие данные о производстве продукции за смену.
Группы рабочих по количеству произведенной продукции за смену, шт. |
Число рабочих |
До 5 |
|
5 – 7 |
|
7 – 9 |
|
9 – 11 |
|
Свыше 11 |
|
Итого 100 |
|
Определите среднюю выработку продукции за смену.
Задача 2. Определите средний размер инвестиций на одно предприятие методом моментов.
Группы предприятий по размеру инвестиций, млрд. руб. |
Число предприятий |
8 – 10 |
3 |
10 – 12 |
4 |
12 – 14 |
5 |
14 – 16 |
6 |
16 – 18 |
7 |
18 – 20 |
8 |
Задача 3. Определить средний возраст рабочих.
Возраст, лет |
До 20 |
20-30 |
30-40 |
40-50 |
50-60 |
Свыше 60 |
Число рабочих |
18 |
120 |
82 |
50 |
20 |
10 |
Задача 4. Вычислите средний объем производства.
Группы бригад по объему производства, млн. руб. |
Число бригад |
До 200 |
10 |
200-400 |
25 |
400-600 |
17 |
600-800 |
14 |
800-1000 |
18 |
1000-1200 |
12 |
Свыше 1200 |
6 |
Задача 5. Определите средний размер заработной платы за месяц одного рабочего.
Размер заработной платы, тыс. руб. |
1400 |
1550 |
1630 |
1750 |
2000 |
Количество рабочих, чел. |
1 |
2 |
4 |
8 |
5 |
Задача 6. Определите способом моментов среднегодовое производство продукции на одно предприятие.
Группы предприятий по объему выпуска, т |
Число предприятий в процентах к итогу |
1000 – 3000 |
12 |
3000 – 5000 |
20 |
5000 – 7000 |
40 |
7000 – 9000 |
18 |
9000 – 11000 |
10 |
Задача 7. Определите по трем предприятиям в целом:
среднее число отработанных рабочими человеко-дней;
среднюю дневную выработку рабочих;
средние затраты на 1 тыс. руб. произведенной продукции.
№ предприятия |
Число рабочих, чел |
Среднее число отработанных рабочими чел.-дней |
Средняя дневная выработка рабочих, тыс. руб. |
Затраты на 1 тыс. руб. продукции, руб. |
1 |
500 |
60 |
25,0 |
90,6 |
2 |
1000 |
64 |
30,0 |
85,4 |
3 |
900 |
62 |
28,0 |
82,0 |
Задача 8. Определите средний процент брака по следующим данным:
Цех |
1 |
2 |
3 |
Процент брака |
0,8 |
1,2 |
0,5 |
Фактическая стоимость продукции, млн. руб. |
125 |
150 |
200 |
Задача 9. Определить средний процент выполнения плана за каждый год.
Кварталы |
2005 г. |
2006 г. |
||
% выполнения плана |
план, млрд. руб. |
% выполнения плана |
факт, млн. руб. |
|
1 |
80,4 |
180,3 |
72,8 |
120,0 |
2 |
90,5 |
195,0 |
75,2 |
108,4 |
3 |
100,2 |
203,2 |
80,4 |
96,2 |
4 |
101,3 |
215,8 |
90,2 |
70,8 |
Задача 10. Определите средние затраты времени на производство 1 тыс. шт. кирпича по 1-й и 2-й группе заводов.
1-я группа |
2-я группа |
||
Затраты времени на производство 1 тыс.шт. кирпича, чел.-ч. |
Производство кирпича, тыс. шт. |
Затраты времени на производство 1 тыс.шт. кирпича, чел.-ч. |
Затраты времени на производство всего кирпича, чел.-ч. |
6,0 |
8000 |
6,5 |
52000 |
6,5 |
12000 |
7,0 |
91000 |
7,2 |
30000 |
7,5 |
450000 |
Задача 11. Определите среднюю себестоимость единицы продукции и среднюю выработку продукции на одного рабочего.
№ предприятия |
Себестоимость, тыс. руб. |
Затраты на всю продукцию, млн. руб. |
Число рабочих |
1 |
13 |
1300 |
400 |
2 |
12 |
1440 |
500 |
3 |
11 |
2200 |
600 |
Задача 12. Определите среднюю себестоимость 1 т пшеницы и среднюю ее урожайность.
№ предприятия |
Затраты на производство пшеницы, тыс. руб. |
Себестоимость 1 т пшеницы, тыс. руб. |
Урожайность пшеницы, ц/га |
1 |
42000 |
18 |
16 |
2 |
62800 |
16 |
19 |
3 |
54300 |
15 |
21 |
Задача 13. Определите среднюю себестоимость 1 кВт-ч и средний расход условного топлива на 1 кВт-ч.
ТЭЦ |
Затраты на выработку электроэнергии, млн. руб. |
Себестоимость 1 кВт-ч, тыс. руб. |
Расход условного топлива на 1 кВт-ч электроэнергии, г. |
1 |
2300 |
0,59 |
430 |
2 |
1000 |
0,60 |
400 |
3 |
2900 |
0,62 |
370 |
4 |
2000 |
0,57 |
320 |
Задача 14. Определите среднюю посевную площадь, среднюю урожайность пшеницы, среднюю себестоимость 1 т пшеницы.
Фермерское хозяйство |
Урожайность, ц/га |
Посевная площадь, га |
Себестоимость 1 т пшеницы, тыс. руб. |
1 |
800 |
20 |
20 |
2 |
1600 |
22 |
15 |
3 |
2000 |
23 |
14 |
Задача 15. Определите средний удельный вес числа специализированных строительных организаций в их общей численности по Минской и по Брестской областям.
Минская область |
Брестская область |
||||
№ района |
общее число строительных организаций |
удельный вес специализированных организаций, % |
№ района |
число специализированных строительных организаций |
удельный вес специализированных организаций, % |
1 |
28 |
50 |
1 |
16 |
64 |
2 |
40 |
55 |
2 |
24 |
40 |
3 |
50 |
42 |
3 |
27 |
45 |
Задача 16. Определите среднюю выработку на одного рабочего в среднем по фабрике за 1-й и 2-й квартал.
1-й квартал |
2-й квартал |
||||
№ цеха |
средняя выработка ткани за смену на 1 рабочего, м |
численность рабочих, чел. |
№ цеха |
средняя выработка ткани за смену на 1 рабочего, м |
выработано ткани за смену, м |
1 |
80 |
100 |
1 |
80 |
12000 |
2 |
80 |
250 |
2 |
85 |
21250 |
3 |
83 |
100 |
3 |
86 |
8600 |
Задача 17. Определите среднюю посевную площадь, среднюю урожайность пшеницы, среднюю себестоимость 1 т пшеницы.
Агрофирма |
Посевная площадь, га |
Валовой сбор, ц |
Затраты на производство всей пшеницы, тыс. руб. |
1 |
1000 |
22000 |
39600 |
2 |
1200 |
20800 |
35360 |
3 |
1100 |
34600 |
51900 |
Задача 18. Определите среднюю урожайность пшеницы, средние затраты труда на 1 га посевной площади, средние затраты труда на 1 ц зерна.
Совхозы |
Валовой сбор, тыс.ц |
Урожайность, ц/га |
Затраты труда, чел.-ч. |
|
на 1 га посевной площади |
на 1 ц зерна |
|||
1 |
3,0 |
21,1 |
34,3 |
1,6 |
2 |
2,2 |
11,4 |
54,4 |
4,7 |
3 |
4,2 |
23,0 |
46,7 |
2,0 |
4 |
1,9 |
13,2 |
67,8 |
5,0 |
Задача 19. Распределение студентов по количеству часов в неделю, затрачиваемых на самостоятельную подготовку к занятиям характеризуется следующими данными:
Бюджет времени, час |
До 20 |
20-25 |
25-30 |
30-35 |
35 и выше |
Число студентов, чел. |
18 |
24 |
42 |
15 |
4 |
Определите моду и медиану.
Задача 20. Определите моду и медиану по следующим данным:
Размер обуви |
33 |
34 |
35 |
36 |
37 |
38 |
39 |
40 |
Число пар, в % к итогу |
4 |
12 |
18 |
26 |
20 |
13 |
5 |
2 |
Задача 21. Определите модальный и медианный уровень заработной планы рабочих цеха
Группы рабочих по заработной плате, тыс.руб. |
350-450 |
450-500 |
550-650 |
650-750 |
750-850 |
850-950 |
Число рабочих, чел. |
5 |
7 |
10 |
12 |
9 |
6 |
Задача 22. Средняя себестоимость продукции одной марки на трех предприятиях, входящих в концерн, соответственно равна 8,7 тыс.руб.; 12,3 тыс.руб.; 14,1 тыс.руб. Определите среднюю себестоимость продукции по концерну в целом, если: 1) на каждом предприятии было произведено одинаковое количество продукции; 2) затраты на выпуск продукции на данных предприятиях одинаковы.
Задача 23. Определите средний объем инвестиций на одно предприятие методом моментов
Группа предприятий по объему инвестиций, тыс.руб. |
Число предприятий, ед. |
1-3 |
3 |
3-5 |
4 |
5-7 |
8 |
7-9 |
7 |
9-11 |
2 |
11-13 |
1 |
Задача 24. При расчете средней величины к каждому значению осредняемого признака было добавлено 30 единиц. Полученные результаты были увеличены в 2 раза. Из преобразованных таким образом величин была рассчитана средняя величина и вес каждой варианты был уменьшен в 3 раза. Полученная после преобразований средняя равна 70.
Определите действительную среднюю величину признака.
Задача 25. В результате инфляции платные услуги населения возросли в 2000 г. в 1,049 раза, в 2001 г. – в 1,09 раз, в 2002 г. – в 1,087 раз, в 2003 г. – в 1,112 раз, в 2004 г. – в 1,129 раз и в 2005 г. – в 1,150 раз. Как изменились цены на платные услуги населению за период с 2000 по 2005 годы.
Задача 26. На обслуживание одного покупателя один продавец расходует 2 мин., второй – 3 мин., третий – 5 мин. Определите средние затраты времени продавцов на обслуживание одного покупателя в течение часа.
Задача 27. Автомобиль с грузом ехал к потребителю со скоростью 30 км/час., обратный путь порожняком на предприятие – со скоростью 40 км/час. С какой средней скоростью проделал весь путь автомобиль?
Задача 28.Автомобиль с грузом выехал к потребителю в соседний район, проделав одну треть пути со скоростью 40 км/час. и два трети пути со скоростью 50 км/час. С какой средней скоростью совершил весь путь к потребителю автомобиль?