Контрольные задания

1.1 а) Доказать, что следующее отображение является метрикой на .

, где

Описать топологию, индуцированную этой метрикой.

б) Пусть - метрика в . Показать, что также является метрикой в

1.2 а) Доказать, что следующее отображение

является метрикой на .

, где

Описать топологию, индуцированную этой метрикой.

б) Пусть - метрика. Показать, что функция также является метрикой.

1.3 а) Доказать, что следующее отображение

является метрикой на .

, где

Описать топологию, индуцированную этой метрикой.

б) Пусть , - метрики. Показать, что функция также является метрикой.

1.4 а) Доказать, что следующее отображение

является метрикой на .

, где

Описать топологию, индуцированную этой метрикой.

б) Пусть - метрика в . Показать, что является метрикой, если удовлетворяет следующим условиям: , монотонно возрастает и , для любых .

1.5 а) Доказать, что следующее отображение

является метрикой на .

, где

Описать топологию, индуцированную этой метрикой.

б) Пусть и метрики в . Показать, что также метрика на .

1.6 а) Доказать, что следующее отображение

является метрикой на .

, где

Описать топологию, индуцированную этой метрикой.

б) Пусть - метрики. Проверить, будет ли метрикой

7. а) Пусть и 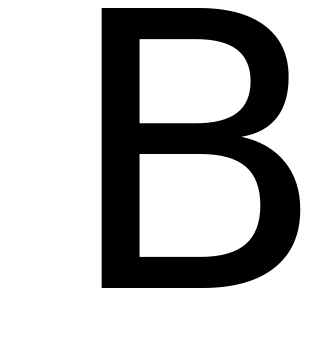- многоугольники на плоскости. Положим 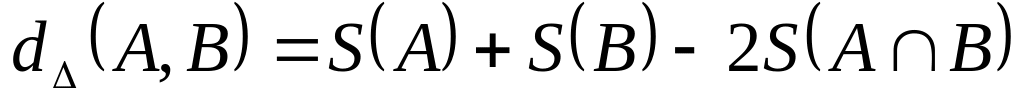, где - площадь многоугольника . Доказать, что 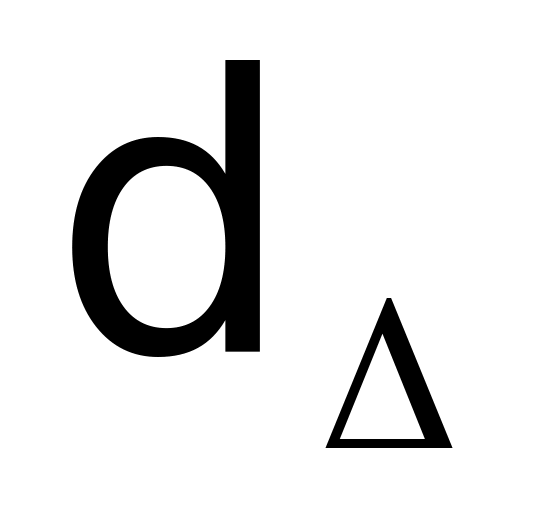- является метрикой на множестве всех плоских многоугольников.

б) Пусть и метрики в . Показать, что также метрика на .

1.8 а) Доказать, что следующее отображение является метрикой на .

Описать топологию, индуцированную этой метрикой.

б) Пусть метрика в . Показать, что также метрика на .

1.9 а) Доказать, что следующее отображение

является метрикой на .

Описать топологию, индуцированную этой метрикой.

б) Пусть и метрики в . Проверить, является ли метрикой на .

1.10 а) Доказать, что следующее отображение

является метрикой на .

.

б) Пусть и метрики в . Проверить, является ли метрикой на .

1.11 а) Пусть - множество всех ограниченных последовательностей действительных чисел. Доказать, что следующее отображение

является метрикой на .

б) Пусть и метрики в . Проверить, является ли метрикой на .

12. а) Доказать, что если на множестве отображение - норма, то , 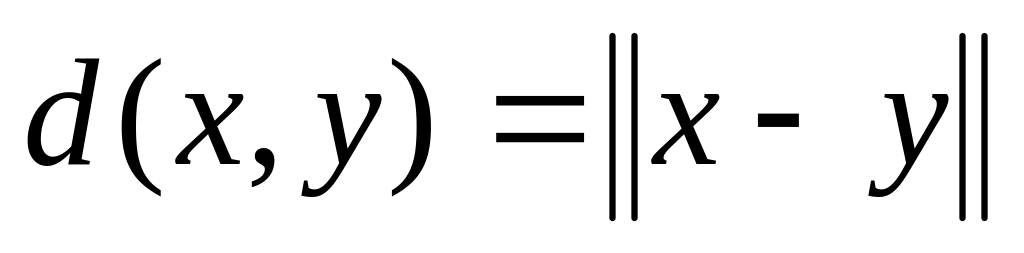- метрика.

б) Пусть и метрики в . Проверить, является ли метрикой на .

1.13 а) Доказать, что следующее отображение является метрикой на .

, где

Описать топологию, индуцированную этой метрикой.

б) Пусть и метрики в . Проверить, является ли метрикой на .

1.14 а) Доказать, что следующее отображение

является метрикой на .

, где

Описать топологию, индуцированную этой метрикой.

б) Пусть и метрики в . Проверить, является ли метрикой на .

1.15 а) Доказать, что следующее отображение

является метрикой на .

Описать топологию, индуцированную этой метрикой.

б) Пусть и метрики в . Проверить, является ли метрикой на .

1.16 а) Доказать, что следующее отображение является метрикой на .

, где

Описать топологию, индуцированную этой метрикой.

б) Пусть - метрика в . Проверить, является ли функция также метрикой в

1.17 а) Доказать, что следующее отображение

является метрикой на .

, где

Описать топологию, индуцированную этой метрикой.

б) Пусть - метрика. Показать, что функция также является метрикой.

1.18 а) Доказать, что следующее отображение

является метрикой на .

, где

Описать топологию, индуцированную этой метрикой.

б) Пусть , - метрики. Показать, что функция также является метрикой.

1.19 а) Доказать, что следующее отображение

является метрикой на .

, где

Описать топологию, индуцированную этой метрикой.

б) Пусть - метрика в . Показать, что является метрикой, если .

1.20 а) Доказать, что следующее отображение

является метрикой на .

, где

Описать топологию, индуцированную этой метрикой.

б) Пусть и метрики в . Показать, что также метрика на , для любых действительных чисел и .

1.21 а) Доказать, что следующее отображение

является метрикой на .

, где

Описать топологию, индуцированную этой метрикой.

б) Пусть - метрики. Проверить, будет ли метрикой

1.22 а) Пусть и - многоугольники на плоскости. Положим , где - площадь многоугольника . Доказать, что - является метрикой на множестве всех плоских многоугольников.

б) Пусть и метрики в . Показать, что также метрика на для любых действительных чисел и .

1.23 а) Доказать, что следующее отображение является метрикой на

.

Описать топологию, индуцированную этой метрикой.

б) Пусть метрика в . Показать, что также метрика на .

1.24 а) Доказать, что следующее отображение

является метрикой на .

Описать топологию, индуцированную этой метрикой.

б) Пусть и метрики в . Проверить, является ли метрикой на .

1.25 а) Доказать, что следующее отображение

является метрикой на .

.

б) Пусть и метрики в . Проверить, является ли метрикой на .

1.26 а) Пусть - множество всех сходящихся последовательностей действительных чисел. Доказать, что следующее отображение

является метрикой на .

б) Пусть и метрики в . Проверить, является ли метрикой на .

27. а) Доказать, что если на множестве отображение - норма, то , - метрика, для любого действительного числа .

б) Пусть и метрики в . Проверить, является ли метрикой на .

1.28 а) Доказать, что следующее отображение является метрикой на .

, где

Описать топологию, индуцированную этой метрикой.

б) Пусть и метрики в . Проверить, является ли метрикой на .

1.29 а) Доказать, что следующее отображение

является метрикой на .

, где

Описать топологию, индуцированную этой метрикой.

б) Пусть , , метрики в . Проверить, является ли метрикой на .

1.30 а) Доказать, что следующее отображение

является метрикой на .

Описать топологию, индуцированную этой метрикой.

б) Пусть и метрики в . Проверить, является ли метрикой на .

1. а) С помощью метрики из задачи 1.1 а) построить открытый шар .

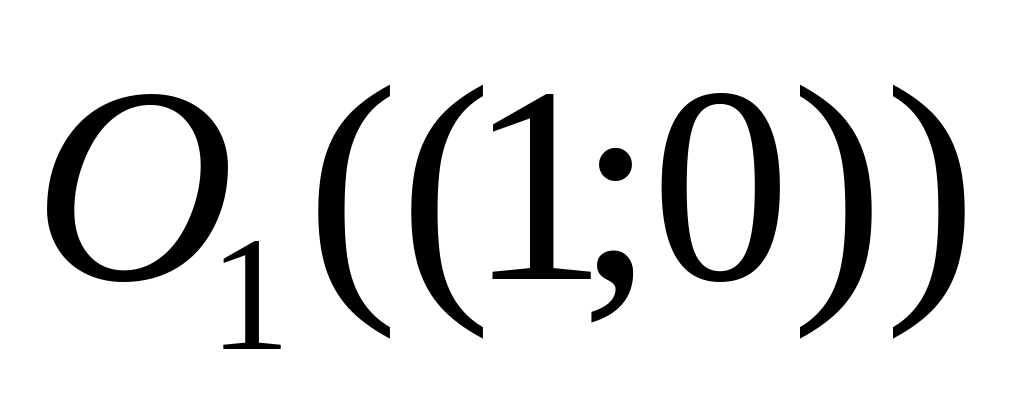б) Показать, что метрики и не порождают одну и ту же топологию.

2. а) С помощью метрики из задачи 1.2 а) построить открытый шар .

б) Пусть - метризуемое пространство. Доказать, что метризуемое одной единственной метрикой тогда и только тогда, когда оно состоит из одной единственной точки.

3. а) С помощью метрики из задачи 1.3 а) построить открытый шар .

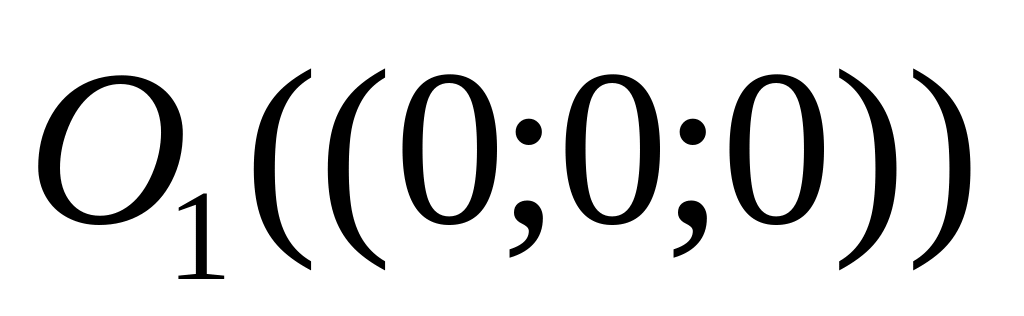б) Пусть - метризуемое пространство. Показать, что если содержит хотя бы две точки, то метрик, метризуемых , бесконечно много.

4. а) С помощью метрики из задачи 1.4 а) построить открытый шар .

б) Показать, что открытый шар является открытым множеством.

5. а) С помощью метрики из задачи 1.5 а) построить открытый шар .

б) Показать, что замкнутый шар является замкнутым множеством.

6. а) С помощью метрики из задачи 1.6 а) построить открытый шар .

б) Показать, что метрики и порождают одну и туже топологию.

7. а) С помощью метрики из задачи 1.7 а) построить открытый шар радиуса единичного квадрата на плоскости.

б) Доказать, что подмножество метрического пространства замкнуто тогда и только тогда, когда предел любой сходящейся в последовательности точек из так же принадлежит .

8. а) С помощью метрики из задачи 1.8 а) построить открытый шар .

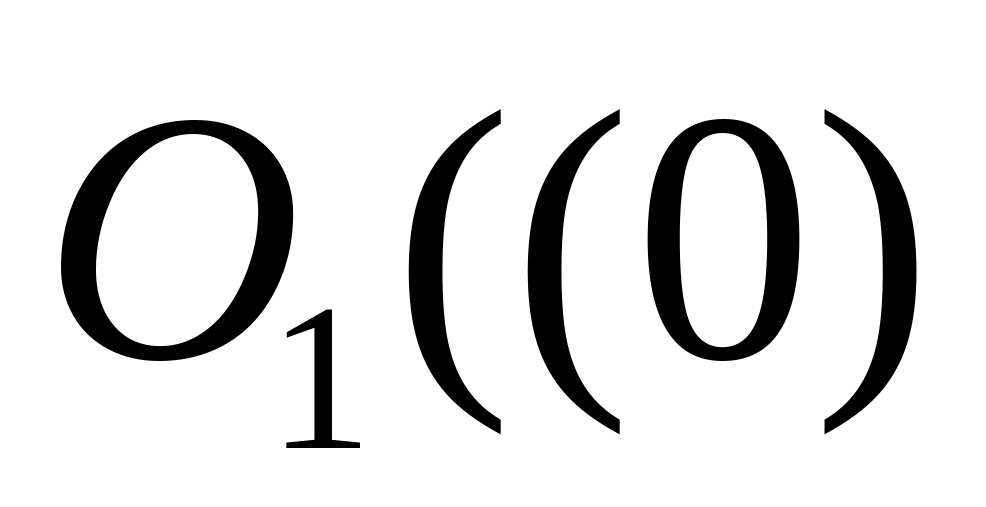б) Доказать, что в метрическом пространстве любое одноточечное множество замкнуто.

9. а) С помощью метрики из задачи 1.9 а) построить открытый шар .

б) Доказать, что точка тогда и только тогда является точкой прикосновения подмножества метрического пространства , когда существует последовательность точек из , сходящаяся к .

10. а) С помощью метрики из задачи 1.10 а) построить открытый шар .

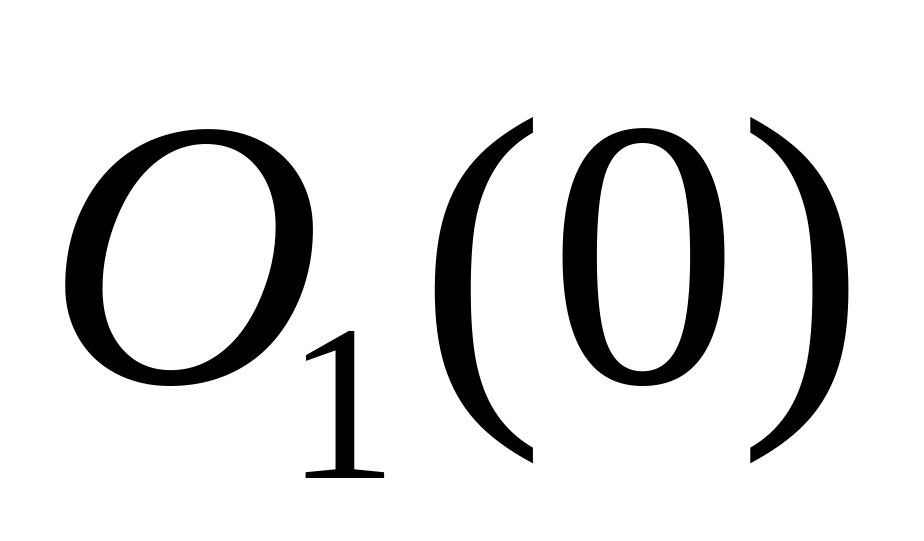б) Пусть - метрическое пространство и . Доказать, что точка тогда и только тогда является точкой прикосновения для множества , когда .

11. а) С помощью метрики из задачи 1.11 а) построить открытый шар .

б) Доказать, что подмножество метрического пространства замкнуто тогда и только тогда, когда для любой точки .

12. а) С помощью метрики из задачи 1.12 а) дать описание открытого шара некоторой точки из пространства .

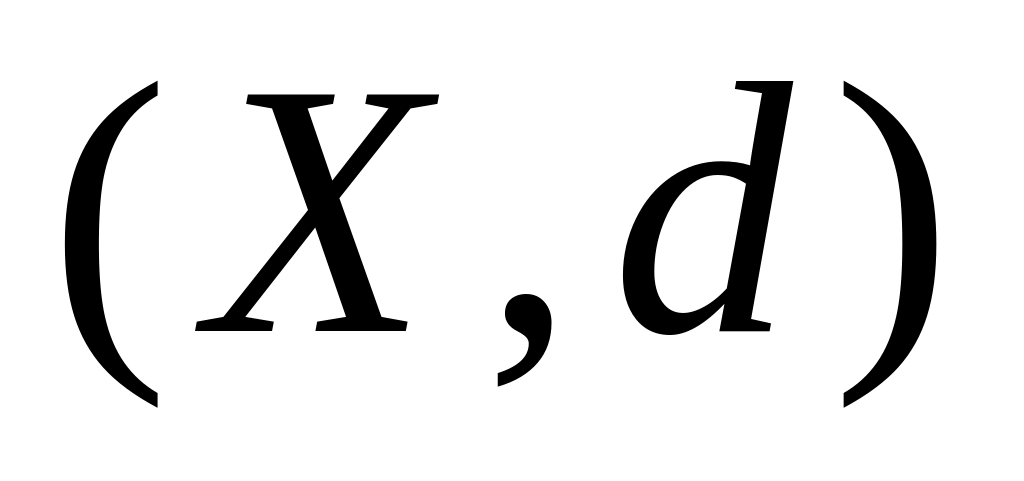б) Привести пример двух замкнутых непересекающихся подмножеств в некотором метрическом пространстве расстояние между которыми равно нулю.

13. а) С помощью метрики из задачи 1.13 а) построить открытый шар .

б) Доказать, что подпространство всех рациональных чисел в евклидовом пространстве не является полным.

14. а) С помощью метрики из задачи 1.14 а) построить открытый шар .

б) Доказать, что - полное метрическое пространство.

15. а) С помощью метрики из задачи 1.15 а) построить открытый шар .

б) Показать, что в метрическом пространстве любые две точки обладают непересекающимися окрестностями.

16. а) С помощью метрики из задачи 1.16 а) построить открытый шар .

б) Показать, что метрики и порождают одну и ту же топологию для любого действительного числа .

17. а) С помощью метрики из задачи 1.17 а) построить открытый шар .

б) Пусть - метризуемое пространство. Доказать, что метризуемо более чем одной единственной метрикой тогда и только тогда, когда оно состоит из более чем одной точки.

18. а) С помощью метрики из задачи 1.18 а) построить открытый шар .

б) Пусть . Построить две различные метрики на .

19. а) С помощью метрики из задачи 1.19 а) построить открытый шар .

б) Показать, что пересечение двух открытых шаров является открытым множеством.

20. а) С помощью метрики из задачи 1.20 а) построить открытый шар .

б) Показать, что дополнение к замкнутому шару является открытым множеством.

21. а) С помощью метрики из задачи 1.21 а) построить открытый шар .

б) Показать, что метрики и порождают одну и туже топологию.

22. а) С помощью метрики из задачи 1.22 а) построить открытый шар радиуса единичного квадрата на плоскости.

б) Пусть - метрическое пространство. Показать, что для любой точки , любого и любого найдется такое , что .

23. а) С помощью метрики из задачи 1.23 а) построить открытый шар .

б) Пусть - множество. Положим , если , и в противном случае. Показать, что метрическое пространство является полным.

24. а) С помощью метрики из задачи 1.24 а) построить открытый шар .

б) Пусть - метрическое пространство, . Доказать, что точка тогда и только тогда, когда .

25. а) С помощью метрики из задачи 1.25 а) построить открытый шар .

б) Доказать, что в метрическом пространстве предел сходящейся последовательности единственен.

26. а) С помощью метрики из задачи 1.26 а) построить открытый шар .

б) Пусть - метрическое пространство, . Доказать, что если существует такое , что для любых , то в нет ни одной предельной точки.

27. а) С помощью метрики из задачи 1.27 а) дать описание открытого шара некоторой точки из пространства .

б) Доказать, что всякое бесконечное ограниченное подмножество числовой прямой имеет предельную точку.

28. а) С помощью метрики из задачи 1.28 а) построить открытый шар .

б) Доказать, что в метрике из задачи 1.28 а) внутренности всевозможных прямоугольников на плоскости являются открытыми множествами.

29. а) С помощью метрики из задачи 1.29 а) построить открытый шар .

б) Доказать, что метрическое пространство - полно тогда и только тогда, когда, когда любая убывающая последовательность замкнутых шаров, радиус которых стремится к нулю, имеет непустое пересечение.

30. а) С помощью метрики из задачи 1.30 а) построить открытый шар .

б) Доказать, что замкнутое множество действительной прямой совершенно в том и только в том случае, когда его смежные интервалы попарно не имеют общих концов.