11

Лабораторная работа 3. Метрические пространства. Основные понятия и определения.

Функция называется метрикой (или расстоянием) в множестве , если:

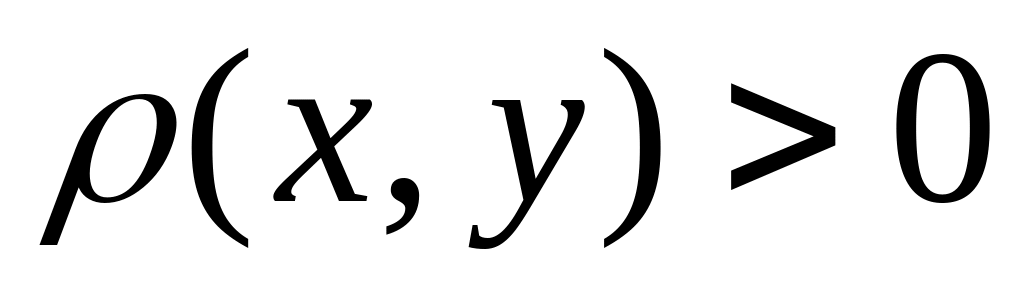1. для любых 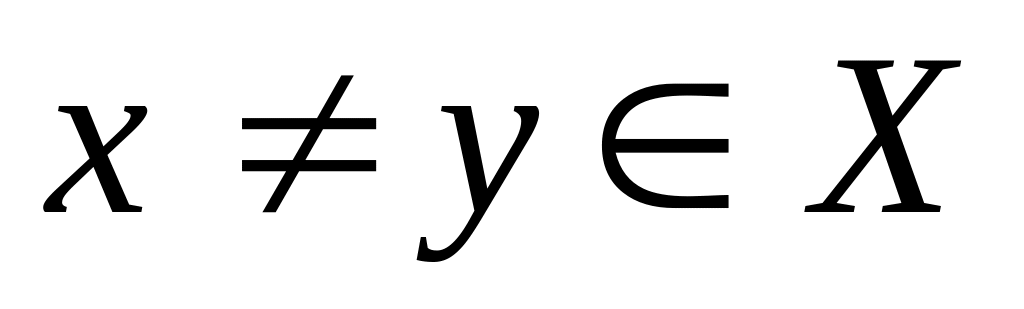и 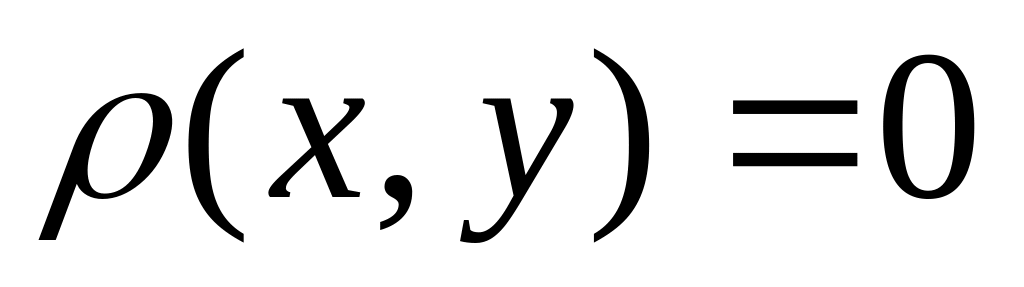тогда и только тогда, когда ;

2. для любых ;

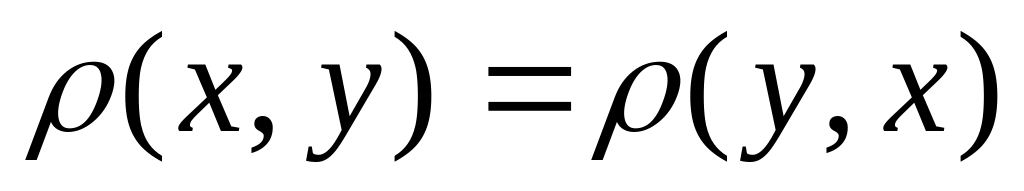3. Для любых ;

Число называется расстоянием между точками и .

Пара , где - метрика в Х, называется метрическим пространством. Условие (3) называется неравенством треугольника.

Пусть - метрическое пространство, - его точка и - положительное вещественное число. Множества , , называются, соответственно, открытым шаром, замкнутым шаром, и сферой пространства с центром в точке а и радиусом .

Метрическое пространство называется вполне ограниченным, если для любого существует такое конечное множество точек из , что .

Множество называется ограниченным, если оно содержится в некотором шаре.

Множество называется открытым в метрическом пространстве , если оно каждую свою точку содержит вместе с некоторым шаром с центром в этой точке.

Множество называется замкнутым в метрическом пространстве , если дополнение к нему в открыто.

Множество пространства называется совершенным, если оно замкнуто и не имеет изолированных точек.

Попарно непересекающиеся множества, границы которых принадлежат дополнительному замкнутому множеству, называются смежными множествами к этому дополнительному замкнутому множеству.

Если - метрическое пространство и , то сужение метрики на является метрикой в и - метрическое пространство. Оно называется подпространством пространства .

Пусть - векторное пространство (над полем R) .Функция : называется нормой, если:

1. для любого 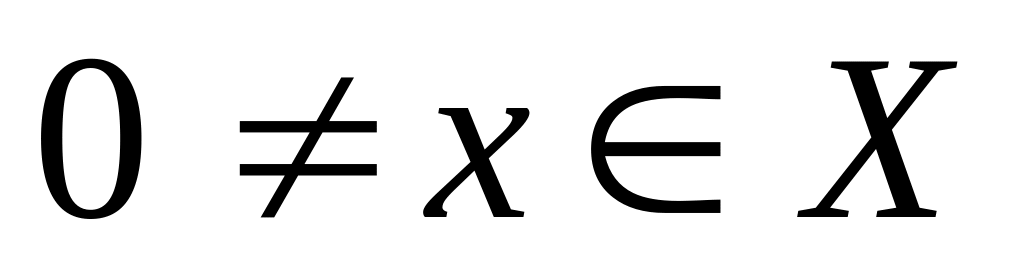, тогда и только тогда, когда ;

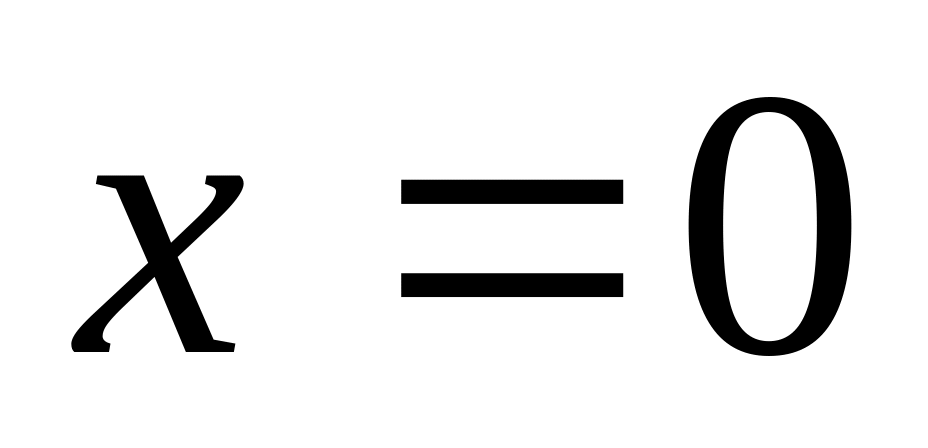2. Для любых ;

3. Для любых .

Векторное пространство с выделенной нормой называется нормированным.

Топологическое пространство называется метризуемым, если его топологическая структура порождается некоторой метрикой.

Две метрики в одном множестве называются эквивалентными, если они порождают одну и ту же топологию.

Пусть - метрическое пространство, . Расстоянием от точки до множества называется число . Оно обозначается через .

Диаметром множества называется число .

Множество ограничено, если .

Пусть - последовательность точек некоторого метрического пространства . Говорят, что эта последовательность сходится к точке ( ), если каждая окрестность точки содержит все точки , начиная с некоторой, т. е. если для любого найдётся такое , что содержит все точки с . Точка называется пределом последовательности . Это определение равносильно тому, что

Последовательность называется фундаментальной, если она удовлетворяет критерию Коши, т. е. если для любого существует такое число , что , для всех , .

Пространство называется полным, если в нём сходится любая фундаментальная последовательность.

Пусть - метрическое пространство. Отображение пространства в себя называется сжимающим отображением, или сжатием, если существует такое число , что для любых двух точек выполняется неравенство

.

Точка называется неподвижной точкой отображения , если